数据结构链表的删、改、查、约瑟夫环、回文链表等常见问题汇总
目录
单链表部分
双向链表部分
其他的常见问题:
约瑟夫环问题
如何判断链表里边存在环
回文链表
单链表部分
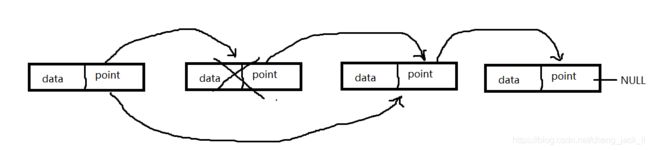
在前两篇的博客中我们初步认识了单链表以及双向链表的基本知识,那么最基本的知识只是带我们简单的认识一下,现在我们来看看链表中的最常见的问题,首先我们来看看单链表的删除某一个结点的操作,以下面的图作以了解。
单链表要想删除其中的某一个结点的话,我们需要找到这个结点的前一个结点,让这个结点的指针域指向所删除的结点的下一个结点的地址,然后再把要删除的结点内存空间释放掉就可以了。可能会有点绕,大家按照上边的图片进行了解就好,这个就是删除链表中的某一个结点,那么还有一个问题就是删除第一个结点呢,删除最后一个结点呢,其实和上边讲的差不多,我们进入函数后接受的指针向后移一位就指向了我们的首元节点,然后就把头结点的指针指向首元结点的后一位结点,再把首元结点释放就好了,但是尾节点就略微麻烦一点,我们要先遍历一遍算出链表的长度,第二遍遍历的时候结束条件就是长度减一,那么我们的指针就指向了倒数第二个结点,然后再把它的指针域指向NULL,再把尾节点释放就好了。
上边说了一大堆,肯定各位已经昏昏欲睡了,我们上代码吧,在代码里边我做一下详细的讲解。
//单链表的删除元素(这是中间删除)
node *delete_node(node *head , int set) /*因为是中间删除,所以我们需要知道到底删除的是哪一
个结点,所以就需要有两个参数,第一个就是把链表传
进来,第二个就是把要删除的结点位数传进来*/
{
node *b = head;
node *p = b;
while(b->next != NULL)
{
set--; /*set是传进来的参数,那么我们每遍历一次对应的set减
一,等到set减到0的时候就是已经找到了要删除的具体
位置*/
if(set == 0)
{
p = b->next;
b->next = p->next;
free(p);
return head;
/*我们设立一个中间变量来存储要删除的结点,把p-
>next给了b->next就是把要删除结点的下一个结点的
地址给了其上一个结点的指针域,这样的话就会把要删
除的结点给孤立起来,然后再把其释放掉,这样核心算
法就完成了,最后返回链表即可*/
}
b = b->next;
}
printf("have not this data\r\n");
return head;
}
//这就是头删
node *delete_head(node *head)
{
node *b = head;
node *p = b->next;
b->next = p->next;
free(p);
return head; /*这里说一下删除首元结点,我们进入链表首先接触到
的就是头结点,那么头结点后移一位就是我们要删除的
首元节点,所以,我们就把p->next赋给b->next这样
的话我们就让原先的首元结点孤立起来了,此时就把它
释放掉即可,最后返回链表*/
}
//然后是尾删
node *delete_wei(node *head)
{
node *b = head;
node *p = head;
int i = 0;
while(b->next != NULL)
{
i++;
b = b->next;
}
while(i>1)
{
p = p->next;
i--;
}
p->next = NULL;
free(b);
return head; /*那么首元结点都就可以删除了,尾结点我们也删除一
下吧,就像我上边说的,删除尾结点的话就要先找到尾
结点在哪里,我们可以使用之前写的求链表长度的算
法,也可以直接遍历一遍,这里不做不多的解释,当我
们找到了链表的长度的时候,此时就可以再次遍历一
遍,但是区别就是此次遍历的结束条件是链表的长度减
一,结束遍历后就找到了倒数第二个结点,那么我们就
把其指针域指向一个NULL,此时尾结点就被孤立了,释
放掉它新的尾结点就是之前的倒数第二挂个结点,最后
返回链表*/
}上边的那么一大堆,我们说了单链表的删除操作,那么现在开始我们来写一下单链表的修改部分,修改也分为三个部分,中部修改,修改首元结点以及修改尾结点的数据,我们可以通过上边的分为三个函数的方法来写,当然了,为了我们代码的多样化,我这里就写成一个函数,那么就牵扯到一个问题就是怎么确定到底是查询哪里的,此处我们使用多分支语句判断一下即可,我们在代码中做详细的解释。
//修改某一个元素
node *modify(node *head , int set)
{
node *b = head;
node *p = head;
int a = 0;
int count = length(head);
while(p->next != NULL)
{
p = p->next;
}
if(set == 0)
{
b = b->next;
printf("please input your number for modify: ");
scanf("%d",&a);
b->data = a;
} /*这里我们看到了set == 0的一个判断语句,就是说
我们要修改的是首元结点的数据,那么我们就把头结指
针后移一位,再直接给其数据域赋值即可*/
else if(set < count)
{
while(1)
{
b = b->next;
set--;
if(set == 0)
{
printf("please input your number for modify: ");
scanf("%d",&a);
b->data = a;
break;
}
}
} /*这里我们可以看到判断条件变成了setdata = a;
} /*这个分支就是要判断是不是尾结点了,尾结点相对于
其他的我感觉简单点,因为我在进入函数后就已经写
了一个指针指向了这个结点的尾结点位置,此时直接
修改即可*/
else if(set > count)
{
printf("your number is so big\r\n");
}
return head;
} 最后的操作就是查询链表内某一个结点的数据元素,这个很简单我就直接上代码了(就是不想码字了,一天了还没吃饭呢)
int search(node *head , int set)
{
node *b = head;
if(set<0||set>length(b))
{
printf("this set is error\r\n");
return -1;
}
while(set>=0)
{
b = b->next;
set--;
if(set == 0)
{
return b->data;
}
}
return 0;
}双向链表部分
好了,单链表的一些操作就先说到这里,我们接下来说一下双向链表的操作,比之单链表更为简单点。为什么说双向链表比之单链表更为简单呢,因为双向链表可以反向遍历啊,我们在上边的单链表里边查找倒数第二个元素的时候怎么查找的,是不是先求出链表的总长度,然后总长度减一再次遍历,这样它不麻烦吗,当然麻烦,所以我们在双向链表中就要对其代码进行优化,为了便于理解,我们通过下边的图来做进一步的理解:
上边的三个图分别对应了我的双向链表的头删、尾删和中间删的基本思路,现在我们详细解释一下,首先来说一下头删的操作,所谓的头删就是删除首元结点,让其下一个结点成为首元结点,那么怎么操作呢,就是把头指针让其指向第二个结点,记住了,我们的首元结点的前驱是指向NULL的,那么就要把第二个结点的前驱改为NULL,那么原先的首元结点就被孤立起来了,此时再把它释放掉,这样一个双向链表的头删操作就完成了,我们写一个伪代码具体看一下:
q = p->next; //这一步就是我们要把链表的第二个元素找出来
q->prior = NULL; //将其前驱指针指向NULL
head->next = q; //让头指针指向新的首元结点
free(p); //释放掉原先的结点上面就是双向链表的头删操作,核心代码很少也很简单,接下来看一下双向链表怎样删除尾部的结点,这个相对于单链表就简单了,我们直接遍历出其尾结点,这个节点就是要释放掉的结点,那么它的上一个结点就是我们新的尾结点,在单链表里面我们重新遍历了一次,在这里就不需要了,我们可以直接使用它的前驱指针就可以找到,我们把它的后继指针指向NULL,这个时候最后一个结点就被我们孤立了,此时就可以将其释放掉,同样我们写一个伪代码做一下具体的讲解:
while(b->next != NULL) //这里的while循环已经是我们的老朋友了,就是找到尾节点的
{
b = b->next;
}
p = b->prior; //前驱给了p,那么p就是倒数第二个结点
p->next = NULL; //p的后继指针域给了NULL,那么b就被孤立了
free(b); //释放掉b头删和尾删已经被过去了,那么中间删还会远吗,下来我们一块儿看一看中间的删除怎么删的,中间删的话要做的操作稍微多了一点,为什么呢,因为不管是头删还是尾删,总有一个指针域是指向NULL的,但是中间删除就不一样了,它的有前驱结点也有后继结点,所以我们在释放结点之前就要做一下简单的操作就是把其前一个结点的后继指针指向它的下一个结点,将其下一个结点的前驱指针指向它的上一个结点,此时这个结点就已经被孤立了,此时才能释放掉这个结点,我们同样使用伪代码进行讲解:
for(int i = 0;inext;
} //这个循环也是我们的老朋友了,不做多的解释
p = b->prior; //b就是我们要删除的结点,那么我们就把其前驱给p,那么b的下一个结点的地址存到p
q = b->next; //同理,把b的后继给q
p->next = b->next; //这里就是要把b的后继给p的后继
q->prior = p; //最后再把p给了q的前驱,此时b已经被孤立
free(b); //释放掉b 通过这样的操作就完成了双向链表的删除某一个结点的操作,下来我们了解一下双向链表的查看某一个结点的数据,这可比删除简单多了,就是找到结点,然后直接返回打印就好,不知道怎么讲,直接上代码吧:
int serch_double(node *head , int set)
{
node *b = head;
if(set == 0)
{
b = b->next;
return b->data;
}
else if(set < double_legth(head))
{
for(int i = 0;inext;
}
return b->data;
}
else if(set == double_legth(head))
{
while(b->next != NULL )
{
b = b->next;
}
return b->data;
}
else if(set > double_legth(head))
{
return -1;
}
return 0;
} 有很多小伙伴肯定已经发现了,既然都能查看的,那修改不就是把数据赋一个新的值么,就是这个道理,我们同样通过代码来看吧:
node *modify(node *head , int set)
{
node *b = head;
if(set == 0)
{
b = b->next;
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set < double_legth(head))
{
for(int i = 0;inext;
}
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set == double_legth(head))
{
while(b->next != NULL )
{
b = b->next;
}
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set > double_legth(head))
{
return NULL;
}
return NULL;
} ok,我们现在把单链表和双向链表的全部代码贴出来以供参考:
单链表部分:
//编程实现一个单链表的创建
#include
#include
typedef struct node
{
int data; //数据域
node *next; //指针域
}node;
node *create()
{
//准备阶段
int i = 0;
node *head , *p , *q;
int x = 0;
head = (node *)malloc(sizeof(node));
//变量分别是:链表中的数据个数、头节点等;
//以下开始进入循环创建每一个节点的数据
while(1)
{
printf("please input the data:");
scanf("%d",&x);
if(x == 0)
{
break;
}
p = (node *)malloc(sizeof(node));
p->data = x;
if(++i == 1)
{
head->next = p;
}
else{
q->next = p;
}
q = p;
}
q->next = NULL;
return head;
}
/*单链表的求长度*/
int length(node *a)
{
node *p;
p = a->next;
int i = 0;
while(p != NULL)
{
i++;
p = p->next;
}
return i;
}
//单链表的节点查找
node *search_node(node *p , int pos)
{
if(pos < 0)
{
printf("参数有误");
return NULL;
}
if(pos == 0)
{
printf("返回头节点");
return p;
}
if(p == NULL)
{
printf("链表有误,这特么就是一个空的");
return NULL;
}
while(pos--)
{
p = p->next;
if(p == NULL)
{
printf("表中没有这个节点");
return NULL;
}
}
return p;
}
void print(node *a)
{
node *p;
p = a->next;
while(p)
{
printf("%d,",p->data);
p = p->next;
}
printf("\n");
}
/*从此开始就是插入操作*/
//首先是头插法
node *inserthead(node *p)
{
node *b = p;
node *a = (node *)malloc(sizeof(node));
a->data = 4;
a->next = b->next;
b->next = a;
return b;
}
//下来是尾插法
node *insertwei(node *p)
{
node *b = p;
node *a = (node *)malloc(sizeof(node));
a->data = 4;
while(b->next != NULL)
{
b = b->next;
}
a->next = NULL;
b->next = a;
return p;
}
//单链表的删除元素(这是中间删除)
node *delete_node(node *head , int set)
{
node *b = head;
node *p = b;
while(b->next != NULL)
{
set--;
if(set == 0)
{
p = b->next;
b->next = p->next;
free(p);
return head;
}
b = b->next;
}
printf("have not this data\r\n");
return head;
}
//这就是头删
node *delete_head(node *head)
{
node *b = head;
node *p = b->next;
b->next = p->next;
free(p);
return head;
}
//然后是尾删
node *delete_wei(node *head)
{
node *b = head;
node *p = head;
int i = 0;
while(b->next != NULL)
{
i++;
b = b->next;
}
while(i>1)
{
p = p->next;
i--;
}
p->next = NULL;
free(b);
return head;
}
//修改某一个元素
node *modify(node *head , int set)
{
node *b = head;
node *p = head;
int a = 0;
int count = length(head);
while(p->next != NULL)
{
p = p->next;
}
if(set == 0)
{
b = b->next;
printf("please input your number for modify: ");
scanf("%d",&a);
b->data = a;
}
else if(set < count)
{
while(1)
{
b = b->next;
set--;
if(set == 0)
{
printf("please input your number for modify: ");
scanf("%d",&a);
b->data = a;
break;
}
}
}
else if(set == count)
{
printf("please input your number for modify: ");
scanf("%d",&a);
p->data = a;
}
else if(set > count)
{
printf("your number is so big\r\n");
}
return head;
}
//查询链表中的数据
int search(node *head , int set)
{
node *b = head;
if(set<0||set>length(b))
{
printf("this set is error\r\n");
return -1;
}
while(set>=0)
{
b = b->next;
set--;
if(set == 0)
{
return b->data;
}
}
return 0;
}
//进入主函数
int main()
{
node *a = create();//创建单链表
node *c = a;
int i = length(a);
printf("长度是:%d\r\n",i);
print(a);
printf("\r\n");
node *b = search_node(c,5);
printf("%d\r\n",b->data);
a = inserthead(a);
print(a);
printf("\r\n");
a = insertwei(a);
print(a);
a = delete_node(a,4);
print(a);
a = delete_head(a);
print(a);
a = delete_wei(a);
print(a);
a = modify(a , 3);
print(a);
a = modify(a , 8);
print(a);
a = modify(a , 12);
print(a);
i = search(a , 5);
printf("your search number is:%d\r\n",i);
return 0;
}
双向链表部分:
#include
#include
using namespace std;
typedef struct node
{
node *prior; //前驱
int data; //数据域
node *next; //后继
}node;
node *create()
{
int x = 0 , i = 0;
node *head , *p , *q;
head = (node *)malloc(sizeof(node));
while(1)
{
cout<<"please input data ";
cin>>x;
p = (node *)malloc(sizeof(node));
p->prior = NULL;
p->next = NULL;
p->data = x;
if(x == 0)
{
break;
}
if(++i == 1)
{
head->next = p;
}
else
{
p->prior = q;
q->next = p;
}
q = p;
}
q->next = NULL;
return head;
}
void display(node *head)
{
node *p = head;
if(head = NULL)
return;
while(p->next != NULL)
{
p = p->next;
}
while(1)
{
cout<data<<" ";
p = p->prior;
if(p->prior == NULL)
{
cout<data<<" ";
break;
}
}
cout<next;
cout<data<<" ";
if(p->next == NULL)
{
break;
}
}
cout<next != NULL)
{
i++;
p = p->next;
}
return i;
}
//双向链表的删除操作
node *delete_node(node *head , int set)
{
node *b = head;
node *p = b->next;
node *q = NULL;
int count = double_legth(head);
if(set == 0)
{
q = p->next;
q->prior = NULL;
head->next = q;
free(p);
return head;
}
else if(set == count)
{
while(b->next != NULL)
{
b = b->next;
}
p = b->prior;
p->next = NULL;
free(b);
return head;
}
else if(set < count)
{
for(int i = 0;inext;
}
p = b->prior;
q = b->next;
p->next = b->next;
q->prior = p;
free(b);
return head;
}
else if(set>count)
{
cout<<"your set is best"<next;
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set < double_legth(head))
{
for(int i = 0;inext;
}
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set == double_legth(head))
{
while(b->next != NULL )
{
b = b->next;
}
cout<<"please input your new data:"<>j;
b->data = j;
return head;
}
else if(set > double_legth(head))
{
return NULL;
}
return NULL;
}
//上边是修改,接下来是查看
int serch_double(node *head , int set)
{
node *b = head;
if(set == 0)
{
b = b->next;
return b->data;
}
else if(set < double_legth(head))
{
for(int i = 0;inext;
}
return b->data;
}
else if(set == double_legth(head))
{
while(b->next != NULL )
{
b = b->next;
}
return b->data;
}
else if(set > double_legth(head))
{
return -1;
}
return 0;
}
int main()
{
node *head = create();
display(head);
cout< 其他的常见问题:
约瑟夫环问题
首先恭喜各位,到此为止呢,我们已经把链表的基本操作了解了,那么在链表中遇到的其他的问题呢,比如说有人突然问了一句链表要是一个循环的呢,这个问题问得好,下来我们就研究一下什么是循环链表,以及它的好处是什么,怎么讲呢,在链表的循环中有一个经典的问题,那就是约瑟夫环的问题,我就这个问题来讲一下循环链表。
所谓的循环链表我单链表的区别是什么呢,我们在建立一个单链表的时候最后一个结点的指针域我们通常会让其指向一个NULL,这样的话就表示其已经终止,那么循环链表的话就是在其最后一个结点的指针域使其指向首元结点的位置,这样就形成了一个环状的链表,我们称之为循环链表,但是切记,千万不可以将头指针释放掉,不然就不知道怎么找到这个链表。
了解了循环链表,我们来看看什么是约瑟夫环,约瑟夫环是将所有的人围成一个环,选取一个厄运数字,从第一个人开始报数,数到厄运数字的人将其杀死,然后其下一个人再从1开始报数,直到最后,当然,约瑟夫环的典故我就不说了,我们主要来看算法,核心算法就是删除中间的元素,我们看看代码
int y = 0;
node *b = head;
printf("please input the eyun number:"); //这个就是我们的厄运数字
scanf("%d",&y);
int k = 1; //这个是报数的,从1开始
while(b->next != b) //结束条件是剩了一个结点
{
k++;
b = b->next; //依次向后遍历
if(k == y)
{
k = 1;
node *a = b->next; //碰到厄运数字的话就把其结点删除
b->next = a->next;
printf("%d ",a->data);
free(a); //删除一个结点的方法就和上边说的一样,不做多的解释
}
}ok,我们来看看约瑟夫环全部的代码,全部的代码就包含俩个部分,一个是创建一个循环链表,另一个就是约瑟夫环,代码如下:
#include
#include
typedef struct node
{
int data; //数据域
node *next; //指针域
}node;
node *create()
{
//准备阶段
int i = 0 , j = 1;
node *head , *p , *q;
int x = 0;
head = (node *)malloc(sizeof(node));
printf("please input people number:");
scanf("%d",&x);
if(x == 0 || x == 1)
{
return NULL;
}
for(;j<=x;j++)
{
p = (node *)malloc(sizeof(node));
p->data = j;
if(++i == 1)
{
head->next = p;
}
else{
q->next = p;
}
q = p;
}
q->next = head->next;
return head;
}
void delete_yt(node *head)
{
//开始删除
int y = 0;
node *b = head;
printf("please input the eyun number:");
scanf("%d",&y);
int k = 1;
while(b->next != b)
{
k++;
b = b->next;
if(k == y)
{
k = 1;
node *a = b->next;
b->next = a->next;
printf("%d ",a->data);
free(a);
}
}
}
int main()
{
node *head = create();
delete_yt(head);
free(head);
return 0;
} 约瑟夫环的问题我们先讲到这里,我的小伙伴可能会发出疑问,既然链表里面有循环链表,那么我把链表的尾指针域随便指向一个结点可不可以,注意,这个是十分危险的,因为他会使得链表里边出现一个环,遍历的时候一旦出现环就会陷入死循环。
如何判断链表里边存在环
这个问题的话有一个比较简单的解法,也是我们最常用的解法,就是使用快慢指针的方法,因为我们都知道一个链表里边一旦存在环的话遍历的时候就会进入死循环,那么我们设定一个快慢指针,如果不存在环的话他们俩是不会碰面的,知道遍历结束,可是如果存在环的话就会碰面,此时就可以判定链表内存在环,程序代码如下:
bool isloop(node *head , node *start)
{
node *p1 = head , *p2 = head;
if(head == NULL || head->next == NULL)
{
return false; //head为NULL或者链表为空的时候直接返回false
}
do
{
p1 = p1->next; //这里就是快慢指针,p1走一步,p2走两步
p2 = p2->next->next;
}while(p2 && p2->next && p1 != p2);
if(p1 == p2)
{
*start = p1; //p1就是环的开始位置
return true;
}
else
{
return false;
}
}回文链表
什么是回文链表呢,我们在生活中经常会遇到一些回文对的诗句等等,意思就是正着读和反着读结果是一样的,这样就是一个回文句,链表也一样,回文链表的意思就是正向遍历和反向遍历的结果是一样的,那么检查的方法有两个,一种是直接遍历两遍的方法,另一个就是采取算法,从中间开始遍历,对于双向链表而言两个指针可以前后自由遍历,对于单链表而言就需要通过链表的逆置算法进行遍历。
以单链表而言,完成算法要做以下准备,1、求出链表的总长度,并找到中间结点
2、将链表的后半段进行逆置
3、判断是否是回文链表
代码如下:
bool hvwflmbc(node* head)
{
// 求链表长度
int len = 0;
for (node *cur = head; cur != NULL; cur = cur->next) {
len++;
}
// 找到链表的中间结点
node *middle = head;
for (int i = 0; i < len / 2; i++) {
middle = middle->next;
}
// 逆置链表的后半部分
node *p = middle;
node *rhead = NULL;
while (p != NULL) {
node *next = p->next;
p->next = rhead;
rhead = p;
p = next;
}
// 判断是否是回文
node *p1 = head;
node *p2 = rhead;
while (p1 != NULL && p2 != NULL) {
if (p1->value != p2->value) {
return false;
}
p1 = p1->next;
p2 = p2->next;
}
return true;
}好的,今天的博客进先写到这里,以上的算法都是我在对其的理解的基础上写出来的,如有问题欢迎评论指出,也欢迎各位能够一块儿探讨。