链表噩梦题之二：约瑟夫环问题

链表噩梦题之二：约瑟夫环问题

提示：2个链表噩梦题之 入环节点问题 后续会说的
所谓噩梦题，就是让你看了怀疑人生，都不想再继续学数据结构与算法了，俗称学习算法劝退题目。

---

---

什么是约瑟夫环问题，它来源于什么故事？

提示：约瑟夫环问题的来源是极为残酷的：

当年罗马帝国是极为强大的，在罗马帝国期间，最出名的就是屠杀被侵略国家的人，罗马人当时以屠杀犹太人为乐子，怎么杀呢？就是约瑟夫环方式来杀：
现在犹太人有i个，比如6个，k=3，从1号开始报数，顺时针报，报到k，杀掉k，继续顺时针从1开始报数，然后循环杀k号，直到只剩下一个人，它就可以活下来。

下面我们演示一波，i=6，k=3时，究竟原始编号1-6，谁能活下来呢？
自然，从1开始数，1,2，3，杀3，黄色那，
然后以黄色从4开始数，新的编号为123，此时刚好数到6，杀6；
然后以绿色开始数，123，恰好数到4，杀4；
然后以紫色开始数，123，恰好数到2，杀2；
然后以粉色开始数，目前只剩下5和1了，123数到5身上，杀5；
仅剩下1了，它可以活下去；

大致约瑟夫环问题就是这样，给你初始人的个数i，报数到k就杀k，请问你最后1–i，哪个号能活下来？

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、审题：约瑟夫环要求什么？

上面已经演示过了，要求这么一个结果int function(i, k),当前有i个人，报数杀掉k，请问你最后哪个号能活下来？

二、解决约瑟夫环问题的数学基础：阶梯循环函数表达式

2.0.约瑟夫环的普通解法o(N*k)

正如最开始演示那样，你最终要杀掉N-1人，每次杀人都要数k次，这样复杂度就是o(N*k) ，过于复杂，我们需要干嘛？
面试自然是想让你优化它的，这么暴力干，你能干到什么时候才知道谁活下来？
尤其是当k很大的时候，你永远数不完了。
因此我们要设计优化算法，目的是要干掉k，使其复杂度降到o(N)。

这么想：
每次杀1人之后，重新报数的话，有一个新的编号x，那在杀人之前这一轮x的旧编号y是多少？能否通过一个数学表达式找到？
不妨设y=f(x)存在，目前我们不知道怎么表达，但是如果这个函数有了，我们可以这么推：
base case：最开始i个人，杀光了i-1个人，现在只剩下i=1个人，新编号x必然是1，因为f(x)存在，所以之前这一轮杀人前，i=2人时，新编号x=1的旧编号y=f(x)就能求出来了【这就是重点】
那么每一轮，这个新编号x，不断地变换自己的身份……
我们一定能反推当i=i人，即初始时刻，这个x它最原始的旧编号y=f(x)是多少？
相当于我们从x=1(i=1)—>x(i=2)–>x(i=3)…–>x(i=i)=y=f(x(i-1))
最终结果就是y。
自然我们的时间复杂度也就是从i=1时，倒着推到i时，遍历了一遍，**o(N)**复杂度。

好，下面我们来找到这个f(x)的表达式，用到的知识就是阶梯循环函数。

2.1.阶梯循环函数

我们先认识一下阶梯循环函数：
y = x % i
它是一个阶梯式的循环函数，有印象的同学，在本科学电子工程设计课程时，当时做面包板连接电路那会，就实现过阶梯电路的。当时示波器显示了一个循环阶梯函数波形图，就算你合格，它的表达式就是这个：
它是这么定义的

也就是说：i的整数倍时，x%i=0，其余都是x，图像如下
不妨设i=3,则0,3，6处都会为0，其余都取x

2.2.根据报数k，求之前被杀的编号s

有了阶梯函数，我们来推到如何根据你报号k，推导被杀这个人的原始编号s

不妨设i=4，k=3，即最开始一共4人，叫到3，就杀s=3

先来看，如果不杀人的话，报号x和编号y之间的关系，一开始从编号1开始喊1号

编号y	报号x
1	1
2	2
3	3
4	4
1	5
2	6
3	7
4	8
显然，你会一直报下去，但是编号永远都是重复周期性的
看函数图长啥样呢？

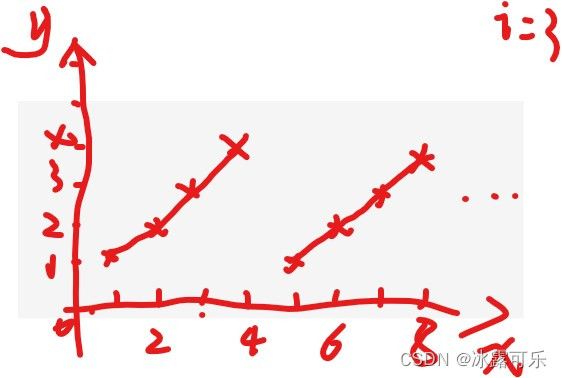显然，这个图，是2.1中图向右平移1个单位，再向上平移1个单位来的，即表达式为

y = (x-1) % i + 1

now，假如有人报了一个数是k，它报k就得杀它，但是它原始编号s是啥呢？显然被杀的s就是

s = (k-1) % i + 1

这就是你报啥k，我轻易给你转换为要杀的这个原始编号s，于是乎，每次被杀死的人就轻易知道是啥蹲在那约瑟夫环中的哪个人了。

2.3.根据活着的最新编号x，求本轮杀人之前x的旧编号y

ok ,有了之前2.1和2.2的知识储备，我们准备推导f(x)，假设本轮杀人后，下一个人开始叫新编号x，我们需要找x在本轮杀人前它的旧编号y，也就是找到f(x)的明确表达式。
先来举个例子，i=7,k=3,叫号，杀人，然后看编号的对应关系
杀之前编号y：1 2 3 4 5 6 7 【7个编号】
杀之后编号x：5 6 × 1 2 3 4 【少了1个号，6个】
注意，这不是喊的号，而是编号，我喊不喊，此时处于我这一轮循环我就得是这个编号
作图看看

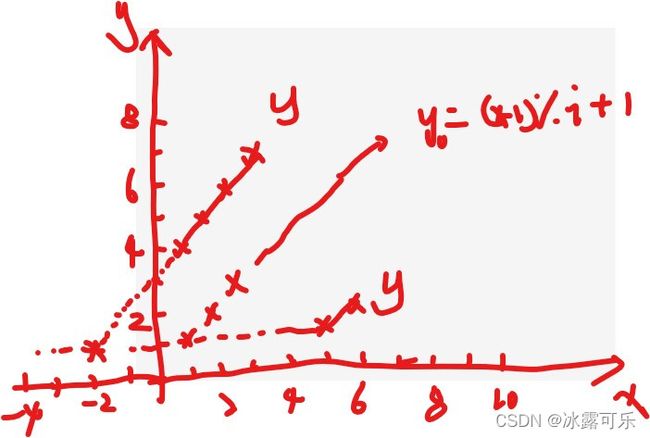
k=s=3，
根据刚刚杀之前y与杀之后xd的对应关系，可以看出，y实际上是y0向左平移3个单位的图，即向左平移s个单位。
所以说
y=(x + s -1) % i + 1
这就是我们要找的表达式f(x)，x是新编号，s是要杀的报号，i是没杀人前的总人数。
根据2.2知道：
s = (k-1) % i + 1
将其带入上面那个式子，则：
y=(x + [(k-1) % i + 1] -1) % i + 1
y=(x + (k-1) % i) % i + 1
y=(x + k-1 ) % i + 1
这里先%再%等于1个%
比如3%2==1, 1%2=1,所以俩%没用的，就一个就行

于是最终我们得到了这个表达式f(x)
y=(x + k-1 ) % i + 1
给定杀人后的新编号x，杀k，杀人前共i个人，请问杀人前x的旧编号y就有明确的表达式了，到这里我们大功告成

最开始你拿到约瑟夫环是一个链表环，你能搞定的信息也就是起始总人数i，你要杀谁k，剩下的旧得不断地去摸索，究竟哪个y能活下来。

我们之前说过倒着求，要求f(i,k),必定先求x=f(i-1,k)，x是新编号，拿着上面那个公式求y即可，递归到最深处，i==1返回1，1就是最新的编号x，返回，不断返回，就能搞定y。下面getLive函数就是f(i,k)。

2.4.约瑟夫环问题的最优解o(N)代码

约瑟夫环的节点定义为：

//啥也不用
    public static class Node{
        public Node next;
        public int id;

        public Node(int i){
            id = i;
            next = null;
        }
    }

给定杀人后的新编号x，杀k，杀人前共i个人，请问杀人前x的旧编号y

public static int getLive(int i, int k){
        //告诉你现在环上i个人，报数到k杀死k，最后活下来那个编号是
        if (i == 1) return 1;//仅仅剩下一个，肯定是它，新编号x==1

        int x = getLive(i - 1, k);//杀死一个，i-1个人时，杀死k号，之后活下来的新编号x
        return (x + k -1) % i + 1;
    }

给你一个约瑟夫环，起点为head，其编号为1，问你最后谁能活下来？
首先，你需要根据环统计总人数i，然后去找那个活下来的原始编号y，断开其余的点，返回y，作为结果

public static Node lastAliveNum(Node head, int k){
        if (head == null || head.next == null || k < 1) return head;

        //统计环的长i
        int i = 1;//cur自己算了
        Node cur = head.next;
        while (cur != head) {
            i++;
            cur = cur.next;
        }

        int num = getLive(i, k);//拿到活下来的号
        while (--num != 0) head = head.next;//让head挪到num那
        head.next = head;

        return head;//返回活下来的节点
    }

上面的代码还是暴力递归，还需要改为动态规划代码，在这大多数就用傻缓存的方式改动态规划代码即可，设定dp[i]代表，有i个人杀k之后能活下来的编号是y=dp[i]，求过dp[i]就不要再去递归求了，直接返回结果。

//傻缓存
    public static int getLiveDP(int i, int k, int[] dp){
        //告诉你现在环上i个人，报数到k杀死k，最后活下来那个编号是

        if (i == 1) {
            dp[1] = 1;
            return dp[1];//仅仅剩下一个，肯定是它
        }

        if (dp[i] != 0) return dp[i];

        int x = getLive(i - 1, k);//杀死一个，i-1个最新活下来的号
        dp[i] = (x + k -1) % i + 1;
        return dp[i];
    }

    public static Node lastAliveNumDP(Node head, int k){
        if (head == null || head.next == null || k < 1) return head;

        //统计环的长i
        int i = 1;//cur自己算了
        Node cur = head.next;
        while (cur != head) {
            i++;
            cur = cur.next;
        }

        int[] dp = new int[i + 1];//不用0

        int num = getLiveDP(i, k, dp);//拿到活下来的号
        while (--num != 0) head = head.next;//让head挪到num那
        head.next = head;

        return head;//返回活下来的节点
    }

测试代码：先建立一个环，再测试

public static Node createCircle(){
        Node head = new Node(1);
        Node n1 = new Node(2);
        Node n2 = new Node(3);
        Node n3 = new Node(4);
        Node n4 = new Node(5);
        head.next = n1;
        n1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = head;//环--4活下去了
        //i==5个节点

        return head;
    }
    public static void test(){
        Node head1 = createCircle();
        Node head2 = createCircle();
        System.out.println(lastAliveNum(head1, 3).id);
        System.out.println(lastAliveNumDP(head2, 3).id);
    }

    public static void main(String[] args) {
        test();
    }

---

总结

提示：本题要掌握的重要知识：

1）阶梯循环函数y = x % i 的图像
2）报号为k，该杀哪个编号的人s?其图像是由1)平移而来的
3）杀人之后的新编号x，对应杀人之前的旧编号y，其图像由2）平移s个单位而来
三个连贯起来，最终得到一个很重要的约瑟夫环，活下来的y编号表达式：
y=(x + k-1 ) % i + 1