搭建SGC实现引文网络节点预测(PyTorch+PyG)

前言

SGC的原理比较简单，具体请见：ICML 2019 | SGC：简单图卷积网络

数据集

数据集采用节点分类常用的三大引文网络：Citeseer、Cora和PubMed，数据集不再详细介绍。

模型实现

PyTorch实现

由于SGC的原理比较简单，因此用PyTorch手写也十分轻松。

观察SGC的表达式：

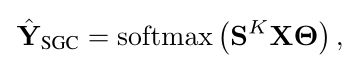
首先我们需要计算对称归一化的邻接矩阵$S$：
$$S={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$
其中$\tilde{A}=A+I$，$\tilde{D}=D+I$。

首先获取数据：

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
names = ['CiteSeer', 'Cora', 'PubMed']

dataset = Planetoid(root='data', name=names[0])
dataset = dataset[0]
edge_index, _ = add_self_loops(dataset.edge_index)

然后提取邻接矩阵：

# get adj
adj = to_scipy_sparse_matrix(edge_index).todense()
adj = torch.tensor(adj).to(device)

提取度矩阵：

deg = degree(edge_index[0], dataset.num_nodes)
deg = torch.diag_embed(deg)
deg_inv_sqrt = torch.pow(deg, -0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
deg_inv_sqrt = deg_inv_sqrt.to(device)

对邻接矩阵进行对称归一化：

s = torch.mm(torch.mm(deg_inv_sqrt, adj), deg_inv_sqrt)

对特征进行预处理：

k = 2
norm_x = torch.mm(torch.matrix_power(s, k), feature)

最后，搭建模型：

class SGC(nn.Module):
    def __init__(self, in_feats, out_feats):
        super(SGC, self).__init__()
        self.softmax = nn.Softmax(dim=1)
        self.w = nn.Linear(in_feats, out_feats)

    def forward(self, x):
        out = self.w(x)
        return self.softmax(out)

其中$x$为上面预处理过的特征norm_x。

模型训练：

def train(model):
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-6)
    loss_function = torch.nn.CrossEntropyLoss().to(device)
    scheduler = StepLR(optimizer, step_size=10, gamma=0.4)
    min_epochs = 10
    min_val_loss = 5
    final_best_acc = 0
    model.train()
    t = perf_counter()
    for epoch in tqdm(range(100)):
        out = model(norm_x)
        optimizer.zero_grad()
        loss = loss_function(out[train_mask], y[train_mask])
        loss.backward()
        optimizer.step()
        scheduler.step()
        # validation
        val_loss, test_acc = test(model)
        if val_loss < min_val_loss and epoch + 1 > min_epochs:
            min_val_loss = val_loss
            final_best_acc = test_acc
        model.train()
        print('Epoch{:3d} train_loss {:.5f} val_loss {:.3f} test_acc {:.3f}'.
              format(epoch, loss.item(), val_loss, test_acc))

    train_time = perf_counter() - t

    return final_best_acc, train_time

PyG实现

首先导入包：

from torch_geometric.nn import SGConv

模型参数：

1. in_channels：输入通道，比如节点分类中表示每个节点的特征数。
2. out_channels：输出通道，输出通道为节点类别数（节点分类）。
3. K：跳数，最远提取到K阶邻居的特征，也就是前面公式中的K。
4. cached：如果为True，则只是在第一次执行时才计算预处理后的特征，否则每一次都计算。默认为True。
5. add_self_loops：如果为False不再强制添加自环，默认为True。
6. bias：默认添加偏置。

于是模型搭建如下：

class PyG_SGC(nn.Module):
    def __init__(self, in_feats, out_feats):
        super(PyG_SGC, self).__init__()
        self.conv = SGConv(in_feats, out_feats, K=k, cached=True)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        x = self.conv(x, edge_index)
        x = F.softmax(x, dim=1)

        return x

训练时返回验证集上表现最优的模型：

def pyg_train(model, data):
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-6)
    loss_function = torch.nn.CrossEntropyLoss().to(device)
    scheduler = StepLR(optimizer, step_size=10, gamma=0.4)
    min_epochs = 10
    min_val_loss = 5
    final_best_acc = 0
    model.train()
    t = perf_counter()
    for epoch in tqdm(range(100)):
        out = model(data)
        optimizer.zero_grad()
        loss = loss_function(out[train_mask], y[train_mask])
        loss.backward()
        optimizer.step()
        scheduler.step()
        # validation
        val_loss, test_acc = pyg_test(model, data)
        if val_loss < min_val_loss and epoch + 1 > min_epochs:
            min_val_loss = val_loss
            final_best_acc = test_acc
        model.train()
        print('Epoch{:3d} train_loss {:.5f} val_loss {:.3f} test_acc {:.3f}'.
              format(epoch, loss.item(), val_loss, test_acc))

    train_time = perf_counter() - t

    return final_best_acc, train_time

实验结果

这里给出Citeseer网络的实验结果：

pytorch train_time: 0.2071399000000005
pytorch best test acc: 0.681

pyg train_time: 0.21978220000000004
pyg best test acc: 0.676

可以看出PyTorch手写和PyG的效果类似，耗时也类似。

完整代码

后面统一整理。