数据探索性分析(EDA)——异常值处理
0 引言
前面有一篇文章介绍单变量分析时,我们提到需要对数据的异常值进行处理,异常值指的是远远偏离整个样本总体的观测值,异常值的存在会降低数据的正态性以及模型的拟合能力等等。异常值的检测主要用箱型图、直方图、散点图等等。今天,本文会介绍异常值的检测以及处理。
1 直方图(正态分布)
1.1 原理
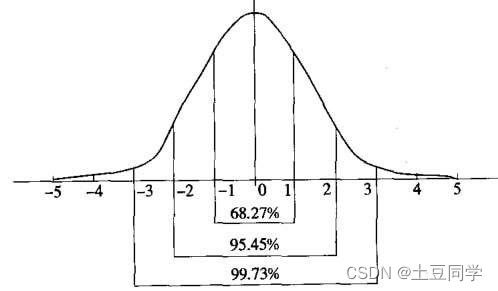
直方图检测异常值的原理主要依据基于正态分布的 3 σ 3σ 3σ法则或 Z − s c o r e Z-score Z−score方法,该方法是假定数据服从正态分布为前提的。首先可以用直方图查看数据分布情况,检查数据是否符合正态分布,并且在数据遵从正态分布的前提下确定异常值,一般可以认为在距离平均值 ( μ ) (μ) (μ)三倍标准差 ( σ ) (σ) (σ)以外的点都是异常值。

不过有些时候,数据虽然符合正态分布,但是并不符合标准正态分布,所以很多时候会把数据进行标准化为标准正态化分布N(0, 1),所以这样就可以很直观地从图中观察到异常值,即区间[-3,3]之外的点都是异常值。
不过实际场景下,真实数据往往并不严格服从正态分布,而均值和标准差的抗干扰性又极小,很容易受到异常值的影响,这种方法对非正态分布数据判断异常值的有效性十分有限,仅适用于正态分布数据。
1.2 实践
(1) 异常值检测
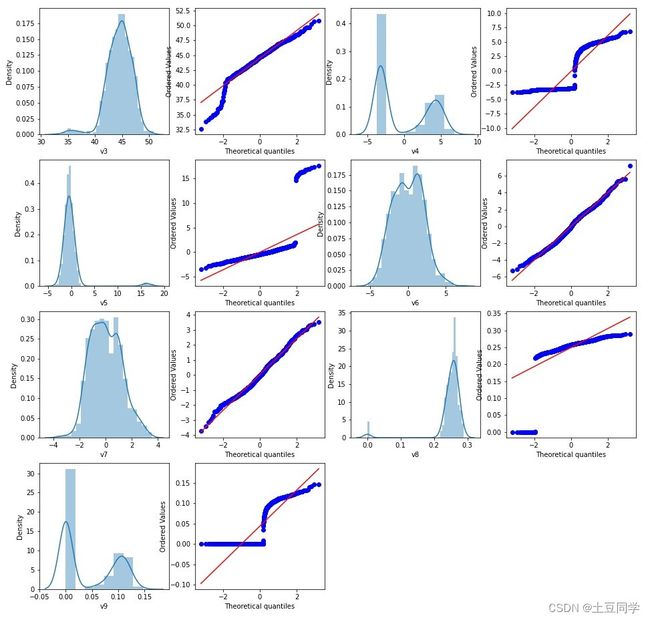
还是用多变量分析中的数据进行分析。我们先总体观察一些连续型变量的分布情况:
numeric_features = ['v3', 'v4', 'v5', 'v6', 'v7', 'v8', 'v9'] # 上篇文章有提到,绘制分布的时候,需要将连续型特征挑选出来
hist_cols = 4
hist_rows = 4
plt.figure(figsize=(4*hist_cols, 4*hist_rows))
i = 0
for col in numeric_features:
i += 1
ax = plt.subplot(hist_rows, hist_cols, i)
ax = sns.distplot(data[col])
ax.set_xlabel(col)
i += 1
plt.subplot(hist_rows, hist_cols, i)
stats.probplot(data[col], plot=plt)
plt.title(' ')
plt.show()
可以看到特征v6、v7是分布形态最好的,最符合正态分布,其次就是特征v3,而特征v5要是没有右边的异常值影响的话,也比较接近正态分布。现在以v3为例,遵从3σ法则将异常值进行删除:
先把v3单独拎出来观察:
plt.figure(1);sns.distplot(data['v3'])
plt.figure(2);stats.probplot(data['v3'], plot=plt)
plt.show()
(1) 异常值处理
然后去计算 μ ± 3 σ μ\pm3σ μ±3σ的区间:
out_up = data['v3'].describe()['mean'] + 3 * data['v3'].describe()['std']
out_down = data['v3'].describe()['mean'] - 3 * data['v3'].describe()['std']
print(out_down, out_up)
37.31668608627181 51.7005326045282
可见在区间[37.32, 51.70]之外的值都是异常值,那我们就根据布尔索引将异常值进行删除:
data_n = data[(data['v3'] >= out_down) & (data['v3'] <= out_up)]
len(data_n)
980
可以看到原本data有1000个样本数据,删除v3的异常值后,就剩下了980条样本数据了。把处理后的数据再次进行绘制:
 可以看到左边的长尾被处理掉了,数据整体分布更加贴近正态分布。
可以看到左边的长尾被处理掉了,数据整体分布更加贴近正态分布。
2 箱型图
2.1原理
与直方图应用场景不同,箱形图的绘制依靠实际数据,不需要事先假定数据服从特定的分布形式,没有对数据作任何限制性要求,它只是真实直观地表现数据形状的本来面貌;另一方面,箱形图判断异常值的标准以四分位数和四分位差为基础,四分位数具有一定的抗干扰性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值对箱型图绘制原理的干扰性较小,因此箱形图识别异常值的结果比较客观。由此可见,相比于直方图,箱形图在识别异常值方面有一定的优越性。
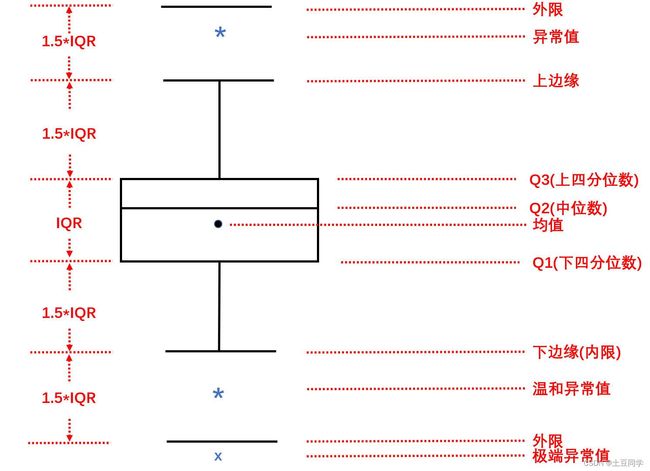
如下图为箱型图的原理图,箱型图以四分位数和四分位距为基础进行异常值的判断。
Q1(下四分位数):25%分位点所对应的值
Q2(中位数):50%分位点所对应的值
Q3(上四分位数):75%分位点所对应的值
IQR(四分位差):IQR=Q3-Q1
上边缘(内限):Q3 + 1.5*IQR
下边缘(内限):Q1 - 1.5*IQR
外限:Q3 + 3 * IQR、Q1 - 3 * IQR
上边缘、下边缘为异常值截断点,称其为内限;在Q3+3IQR和Q1-3IQR处称为外限。处于上下边缘即内限以外的点都是异常值,其中在内限与外限之间的异常值为温和的异常值(mild outliers),在外限以外的为极端的异常值(extreme outliers)。在图中用“*”表示温和异常值,“x”为极端异常值,并且各分位点以及内外限均在图中标出。
2.2 实践
(1) 异常值检测
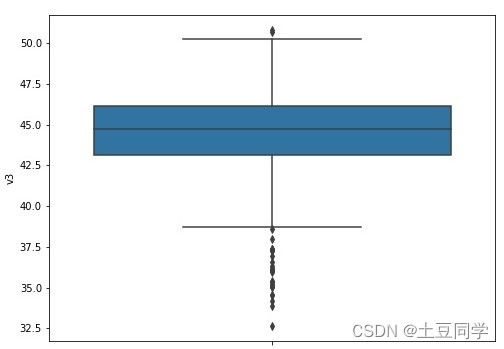
以特征v3为例进行箱型图的绘制:
plt.figure(figsize=(8, 6))
sns.boxplot(y=data['v3'])
plt.show()
可以看到v3在上下边缘之外都存在异常值,其中下边缘的异常值比较多,接下来就可以对异常值进行处理。
(2) 异常值处理
在实际绘制过程中,boxplot会展示内限之外的所有异常值但不会去区分温和异常值和极端异常值,不过在进行删除的时候,可以人为选择是只删除极端异常值或者所有异常值。
小编将处理方法包装成了一个处理函数,方便以后调用:
def box_outliers(data, fea, scale):
'''
data: DataFrame,需要处理的数据表格
fea: 需要处理的特征
scale: 删除尺度
return: 异常值删除后的数据表格
'''
Q1 = data[fea].quantile(0.25)
Q3 = data[fea].quantile(0.75)
IQR = Q3 - Q1
data = data[(data[fea] >= Q1 - scale * IQR) & (data[fea] <= Q3 + scale * IQR)]
return data
包装后进行调用:
data_x = box_outliers(data, 'v3', 1.5)
len(data_x)
973
这里小编选择删除内限之外的所有异常值,所以scale选择了1.5,如果scale选择3的话,则仅仅删除极端异常值,保留温和异常值。
再次把处理完的数据进行可视化:
plt.figure(1);sns.distplot(data_x['v3'])
plt.figure(2);stats.probplot(data_x['v3'], plot=plt)
plt.show()
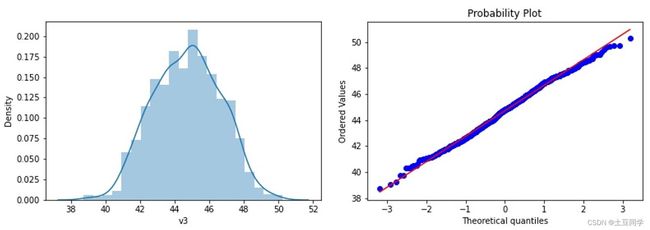 可以发现因为删除的异常值比较多,所以可视化的效果是好于上一个方法的,但是删除后对于业务实际的效用如预测、分类等等的好坏就需要在实践中进行体现,并不是一定说我把所有异常值都删除了效果就一定好。
可以发现因为删除的异常值比较多,所以可视化的效果是好于上一个方法的,但是删除后对于业务实际的效用如预测、分类等等的好坏就需要在实践中进行体现,并不是一定说我把所有异常值都删除了效果就一定好。
3 散点图
3.1 原理
箱型图用于分析单个变量或特征中的异常值,但如果现在有一组特征如(面积, 房价)、(身高, 体重)等等,这时候我们可以用散点图进行分析,原因是因为实际业务中,用箱型图进行单个变量分析的时候,数据可能不是异常值,但是当数据处于实际环境中,比如(身高, 体重),身高150,体重100kg,在进行单个变量分析的时候,身高体重其实都没问题,但是放在一起的话,可能就会偏离整体观察值比较远,成为异常值。
3.2 实践
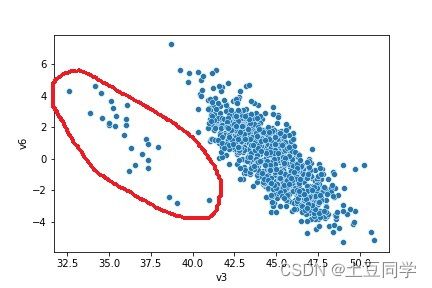
散点图只能对数据进行大致观察,而没有处理的相关依据,要处理的话需要依靠其它离群点的检测和处理算法如聚类算法、K-means算法、孤立森林、One Class SVM算法等等。本文就介绍一些比较简单直接的方法,具体与算法相关的内容会在后面文章进一步介绍。所以,这里就简单绘制一下散点图,但是因为我们使用的实例数据没有实际意义,与业务场景不挂钩,所以我只是以这个图进行形式上的理解,绘制v3、v6的散点图:
sns.scatterplot(data['v3'], data['v6'])
plt.show()
4 异常值的其他处理方法
前面简单介绍了一下如何检测异常值,并且将异常值进行删除。但是异常值的处理方法并不只有一种,还有其他方法如转换、分桶、填充等等。
删除除了上面直方图中用到的3σ法则还有一个封顶方法,将5%分位~95%分位以外的数据都当作为异常值进行删除。
数据转换可以减轻或者消除异常值的影响,如数据取对数、平方根等等,一些不好的数据分布形态在进行数据转换后可能会有所改善。
分桶的原理类似于数据转换,广义上其实也属于其范围。数据分桶可以把数据进行离散化,消除个别异常值的影响,离散后的特征对异常值更具鲁棒性,比如[5, 9, 50, 23, 45, 33, 100, 28, 19, 21, 36, 51, 32 ],此时可以以10为间隔进行分桶并将>50的都分为一桶,所以异常值100 就不会对模型造成很大的干扰并且也不会因为个别数据的改变而产生较大影响。
填充方法在缺失值处理中用得比较多,在异常值处理中用得相对较少。在填充之前需要知道异常值是自然形成还是认为造成的,若是人为造成,则可以进行填充,填充方法不固定如众数、中位数、预测、插值等等。
50, 23, 45, 33, 100, 28, 19, 21, 36, 51, 32 ],此时可以以10为间隔进行分桶并将>50的都分为一桶,所以异常值100 就不会对模型造成很大的干扰并且也不会因为个别数据的改变而产生较大影响。
填充方法在缺失值处理中用得比较多,在异常值处理中用得相对较少。在填充之前需要知道异常值是自然形成还是认为造成的,若是人为造成,则可以进行填充,填充方法不固定如众数、中位数、预测、插值等等。