2021年大数据挑战赛A题智能运维中的异常检测与趋势预测求解全过程论文及程序

2021年大数据挑战赛

A题 智能运维中的异常检测与趋势预测

原题再现：

  异常检测（异常诊断/发现）、异常预测、趋势预测，是智能运维中首当其冲需要解决的问题。这类问题是通过业务、系统、产品直接关联的 KPI 业务指标进行分析诊断，指标主要包括用户感知类（如页面打开延时）、服务性能（如用户点击量）、服务器硬件健康状况（如 CPU 利用率、内存使用率）等关键性能指标。
  不同场景的运维，分析的指标种类差异较大，但都具备时序性特点，不同场景的 KPI 指标，以毫秒、秒、分钟、小时、天为时间间隔的数据序列都会出现，有些复杂场景的业务，往往会混合多个时间间隔的数据，但均为随时间变化而变化的时序数据。
  本次赛题以运营商基站 KPI 的性能指标为研究数据，数据是从 2021 年 8 月28 日 0 时至 9 月 25 日 23 时共 29 天 5 个基站覆盖的 58 个小区对应的 67 个 KPI指标。其中，选取三个核心指标进行分析。
  第一个指标：小区内的平均用户数，表示某基站覆盖的小区一定时间内通过手机在线的平均用户人数；
  第二个指标：小区 PDCP 流量，通过小区 PDCP 层所发送的下行数据的总吞吐量(比特)与 小区PDCP层所接收到的上行数据的总吞吐量(比特)两个指标求和得到，表示某基站覆盖的小区在一定时间内的上下行流量总和；
  第三个指标：平均激活用户数，表示某基站覆盖的小区在一定时间内曾经注册过无线网络的平均人数。
  针对上面三个指标，完成如下 3 个问题：
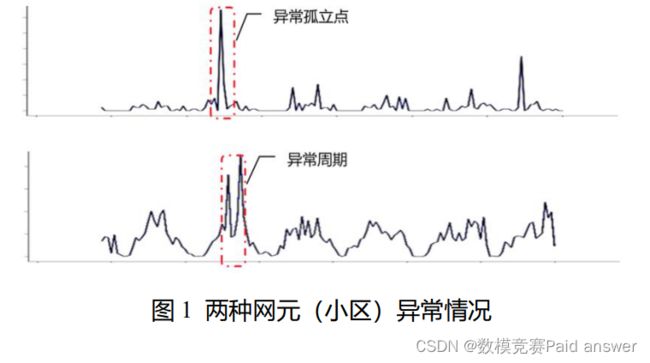
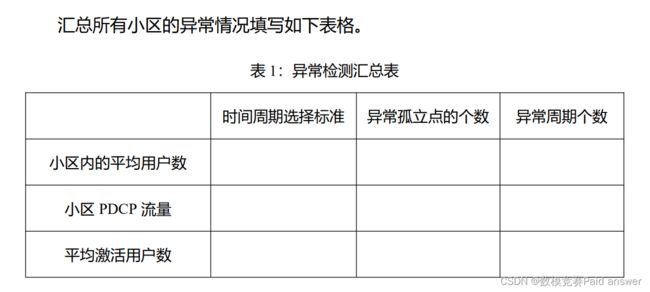
  问题 1 异常检测：利用附件的指标数据，对所有小区在上述三个关键指标上检测出这 29 天内共有多少个异常数值，其中异常数值包含以下两种情况：异常孤立点、异常周期。


  问题 2 异常预测：针对问题 1 检测出的异常数值，通过该异常数值前的数据建立预测模型，预测未来是否会发生异常数值。异常预测模型除了考虑模型准确率以外，还需要考虑两点：1）模型输入的时间跨度，输入数据的时间跨度越长，即输入数据量越多，模型越复杂，会增加计算成本和模型鲁棒性，降低泛化能力；2）模型输出时间跨度，即预测的时长，如果只能精准预测下一个时刻是否发生异常，在时效性上则只能提前一个小时，时效性上较弱。
  问题 3 趋势预测：利用 2021 年 8 月 28 日 0 时至 9 月 25 日 23 时已有的数据，预测未来三天（即 9 月 26 日 0 时-9 月 28 日 23 时）上述三个指标的取值。并完整填写附件 2 中的预测值表格，单独上传到竞赛平台。
  说明：
  （1）异常孤立点，在一段时间内仅有 1 个异常值；异常周期，在一段时间内有多个异常值。（时间范围、异常值范围需要参赛者自行设定并说明理由）。
  （2）在异常预测和趋势预测时，可借用其他指标作为辅助输入特征建模，如预测第 i 个指标第 t 时刻的数值或是否异常，可使用第 j 个指标 t 时刻前的数值作为输入，但不能以第 j 个指标第 t 时刻及之后的数值作为输入。
  （3）异常预测和趋势预测建模时，需考虑每个小区、基站之间的差异。可以针对每个小区、基站单独建模，也可以统一建模，最终以模型评价指标来评估。
  （4）第一题和第二题以 F1 值（2精确率召回率/（精确率+召回率））来评估模型优劣，第三题以 MAPE（平均绝对百分比误差）作为模型评估指标。

整体求解过程概述(摘要)

  在智能运维中，通过与业务、系统、产品关联的KPI业务指标时间序列数据进行分析可以进行异常检测、异常预测和趋势预测。本文研究了运营商基站KPI业务从2021年8月28日0时至9月25日23时共29天5个基站覆盖的58个小区对应的三个核心性能指标，通过DBSCAN密度聚类算法、LOF算法和Prophet模型对三个核心关键指标进行了异常值检测、异常值预测、趋势预测。
  在问题一中，题目要求对异常点检测，我们利用寻找异常点的模型进行求解，在众多模型中，我们选取LOF，Isolation Forest(孤立森林)，DBSCAN(密度聚类)三个模型分别对指标进行异常检测，通过比较三个模型的检测效果，发现针对不同的小区，不同指标的数值三个模型的效果各有所优势。考虑到现实的情况，我们不把深夜时间段的数值低谷期当做异常点，而认为这是业务正常现象，在三个模型中综合考虑，认为使DBSCAN密度聚类算法较为合适，但是在对某些小区进行异常点预测时存在误差，需要对异常值检测结果进行修正。而对时间周期的标准定义，我们也是根据实际业务情况，发现指标的时间序列数据有一定的日周期性，为此我们把时间序列数值进行分解求出周期性，而求出的周期的时间跨度来作为异常周期的时间跨度，从而来计算异常周期的个数。
  在问题二中，题目要求预测未来的异常点，我们把题目一所找出的异常点进行0-1标记，0代表该时间点的指标数值不是异常，1则表示异常。我们建立神经网络模型进行求解，题目要求模型即要输入时间跨度少，又要在时效性上高，因此为了能确定模型的最佳输入时间跨度和最佳输出时间跨度，我们采用交叉验证法与网格搜索法，通过比较不同的时间跨度的模型算法的F1值来选择最佳时间跨度，最终确定最佳方案是输入时间跨度为10小时，输出时间跨度为5小时，即神经网络的输出是前10个小时的数值，输出是后5个小时的异常点标记。
  在问题三中，使用prophet算法，把第一问中检测出的异常数据点和正常数据点作为数据输入，分析数据中的日季节性、假期性和整体趋势性，并建立预测模型，对未来三天三个核心指标的数据进行预测。为了验证模型的预测效果，使用交叉验证方法对模型的预测效果进行评估，计算出预测值的MSE值和MAPE值，其数值均较小，说明模型预测效果较好

模型假设：

  （1）本题中所有小区之间仅存在物理性能上的 KPI 差异，不存在人为的外来影响因素和节假日活动、政策的影响。
  （2）本题中服务器本身的运作是稳定的，不存在异常的流量访问导致的异常。
  （3）本题中 58个小区之间的区别仅仅在于 KPI的性能和小区人员的日常使用习惯和人数问题，不存在其他的影响因素

问题分析：

  问题一的分析
  题目要求我们对关于时间序列的三个关键指标进行异常点的检测，对此我们想到异常点检验算法的类别，其中常见的三个分别为：1.基于统计学的方法，根据已知数据来构建一个概率分布模型，把具有低概率的数据视为异常点。2.基于聚类的方法，把偏离聚类的离散点作为异常点。3.基于专门的异常点检测算法，其代表是 One Class SVM和孤立森林(Isolation Forest)。我们分别用 LOF，孤立森林(Isolation Forest)，DBSCAN 三个模型在对所有小区的三个指标进行异常预测，比较三个模型之间的对异常点检测的效果，由于每个小区、基站之间存在差异，所以对每个小区、基站使用以上三种方法分别单独建立三个异常检测模型，根据实际业务情况从三个模型中选择最适合每个小区的模型。再次考虑到实际业务的因素，三个关键指标有一定的日周期性，我们根据异常点的分布来选取最佳的时间周期，来确定异常点的周期个数。

  问题二的分析
  对于问题二，在问题一的基础上对已检测的异常点进行标记，这里我们将异常点标记为1，非异常点标记为0，这样就有一组数据{0,1}关于时间序列变化。首先对于预测异常来说，输入项是前一段时间的指标的具体数值，输出项是未来时间点可能出现的异常点。模型的选取上既要考虑输入数据的时间跨度，即为了减少模型的复杂度和计算成本应减少输入指标数据量尽可能地少，又要考虑到输出数据的时间跨度（时效性）和数据的准确度，即在保证准确度的情况下，对未来预测的时间跨度应尽可能地长。为此我们选取神经网络进行预测，输入层为数据时间跨度的具体值，输出层为未来预测的异常点标签0或1。

  问题三的分析
  第三题需要根据29天的历史数据建立模型，预测未来三天的数据，题目以运营商基站KPI的性能指标为研究数据，并且选择其中三个核心指标进行分析，因此使用prophet算法对三个核心指标分别建立数据预测模型进行预测。对三个指标数据的时间序列图进行观察分析发现，指标数据的变化趋势分为日季节性和整体趋势性，因此使用时间序列的分解方法将指标的时间序列数据分为日季节项代表周期性变化，趋势项用于拟合时间序列里的非周期项，剩余项代表了所有未被模型考虑到的误差元素，并将历史数据作为输入，求出以上几项并进行求和得到预测模型并输出预测结果。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分程序如下:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import copy
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import KMeans,DBSCAN,AgglomerativeClustering
import scipy.cluster.hierarchy as sch
# v测量，轮廓系数
from sklearn.metrics import v_measure_score, silhouette_score

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = 'False'

def Dbscan():
    X1, y1 = ds.make_circles(n_samples=5000, factor=.6, noise=.05)
    X2, y2 = ds.make_blobs(n_samples=1000, n_features=2, centers=[[1.2, 1.2]],
                                 cluster_std=[[.1]], random_state=9)
    X = np.concatenate((X1, X2))
    plt.scatter(X[:, 0], X[:, 1], marker='o')
    plt.title('原始数据样本点分布')
    plt.show()

    y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.title('K-means算法进行聚类处理')
    plt.show()

    y_pred = DBSCAN().fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.title('默认参数密度聚类')
    plt.show()

    y_pred = DBSCAN(eps=0.08, min_samples=3).fit_predict(X)  # eps = 0.08 半径, min_samples=3样本数量
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.title('设置参数的密度聚类')
    plt.show()

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可