梯度下降法介绍（ 案列：波士顿放假预测）

目录

一、详解梯度下降算法

1.1 梯度下降饿相关概念复习

1.2 梯度下降法流程的推导

二、 梯度下降法大家族

2.1 全梯度下降算法(FG)

2.2 随机梯度下降算法(SG)

2.3 小批量梯度下降算法(mini-batch)

2.4 随机平均梯度下降算法(SAG)

三、案列：波士顿房价预测

3.1 案列背景

3.2 案列分析

3.3 回归性能评估

3.3 代码实现

---

一、详解梯度下降算法

1.1 梯度下降饿相关概念复习

在详细了解梯度下降的算法之前， 我们先复习相关的⼀些概念。

• 步长(Learning rate)：

    步长决定了在梯度下降迭代的过程中， 每⼀步沿梯度负方向前进的⻓度。 用之前帖子的下山列子， 步⻓就是在当前这⼀步所在位置沿着最陡峭最易下⼭的位置⾛的那⼀步的⻓度。

• 特征(feature)：

    指的是样本中输⼊部分， 比如2个单特征的样本则第⼀个样本特征为x ， 第⼀个样本输出为y 。

• 假设函数(hypothesis function)：

    在监督学习中， 为了拟合输⼊样本， 而使用的假设函数， 记为。 比如对于单个特征的m个样本可以采⽤拟合函数如下：

• 损失函数(loss function)：

    为了评估模型拟合的好坏， 通常用损失函数来度量拟合的程度。 损失函数极小化， 意味着拟合程度最好， 对应的模型参数即为最优参数。
    在线性回归中， 损失函数通常为样本输出和假设函数的差取平⽅。 ⽐如对于m个样本(x , y )(i = 1, 2, ...m)， 采⽤线性回归， 损失函数为：

                                                        

其中x 表示第i个样本特征， y 表示第i个样本对应的输出， h (x )为假设函数。
 

1.2 梯度下降法流程的推导

1) 先决条件： 确认优化模型的假设函数和损失函数。

比如对于线性回归， 假设函数表示为  , 其中为模型参数，为每个样本的n个特征值。 这个表示可以简化， 我们增加⼀个特征， 这样

同样是线性回归， 对应于上⾯的假设函数， 损失函数为：

2) 算法相关参数初始化
主要是初始化算法终⽌距离ε以及步长α 。 在没有任何先验知识的时候， 我喜欢将所有的θ 初始化为0， 将步长初始化为1。 在调优的时候再 优化。

3) 算法过程：
3.1) 确定当前位置的损失函数的梯度， 对于 ,其梯度表达式如下：

3.2) ⽤步⻓乘以损失函数的梯度， 得到当前位置下降的距离， 即

3.3) 确定是否所有的,梯度下降的距离都⼩于ε， 如果⼩于ε则算法终止， 当前所有的)即为最终结果。 否
则进⼊步骤4.

4)更新所有的θ ， 对于， 其更新表达式如下。 更新完毕后继续转⼊步骤1

下面用线性回归的例⼦来具体描述梯度下降。 假设我们的样本是:

损失函数如前⾯先决条件所述：

则在算法过程步骤1中对于 的偏导数计算如下：

由于样本中没有上式中令所有的 为1.
步骤4中 的更新表达式如下：

从这个例⼦可以看出当前点的梯度⽅向是由所有的样本决定的， 加 是为了好理解。 由于步⻓也为常数， 他们的乘积也为常数， 所以这⾥可以用⼀个常数表示。

二、 梯度下降法大家族

⾸先， 我们来看⼀下， 常⻅的梯度下降算法有：
全梯度下降算法(Full gradient descent),
随机梯度下降算法(Stochastic gradient descent),
⼩批量梯度下降算法(Mini-batch gradient descent),
随机平均梯度下降算法(Stochastic average gradient descent)
它们都是为了正确地调节权重向量， 通过为每个权重计算⼀个梯度， 从⽽更新权值， 使⽬标函数尽可能最⼩化。 其差别在于样本的使⽤⽅式不同。

2.1 全梯度下降算法(FG)

批量梯度下降法， 是梯度下降法最常⽤的形式， 具体做法也就是在更新参数时使⽤所有的样本来进⾏更新。
计算训练集所有样本误差， 对其求和再取平均值作为目标函数。
权重向量沿其梯度相反的⽅向移动， 从⽽使当前⽬标函数减少得最多。
其是在整个训练数据集上计算损失函数关于参数θ 的梯度：

由于我们有m个样本， 这⾥求梯度的时候就⽤了所有m个样本的梯度数据
注意：

• 因为在执⾏每次更新时， 我们需要在整个数据集上计算所有的梯度， 所以批梯度下降法的速度会很慢， 同时， 批梯度下降法⽆法处理超出内存容量限制的数据集。
• 批梯度下降法同样也不能在线更新模型， 即在运⾏的过程中， 不能增加新的样本。

2.2 随机梯度下降算法(SG)

由于FG每迭代更新⼀次权重都需要计算所有样本误差， ⽽实际问题中经常有上亿的训练样本， 故效率偏低， 且容易陷⼊局部最优解， 因此提出了随机梯度下降算法。
其每轮计算的⽬目标函数不再是全体样本误差， 而仅是单个样本误差， 即每次只代⼊计算⼀个样本⽬标函数的梯度来更新权重， 再取下⼀个样本重复此过程， 直到损失函数值停⽌下降或损失函数值小于某个可以容忍的阈值。
此过程简单， 高效， 通常可以较好地避免更新迭代收敛到局部最优解。 其迭代形式为
 

但是由于， SG每次只使⽤⼀个样本迭代， 若遇上噪声则容易陷⼊局部最优解。

2.3 小批量梯度下降算法(mini-batch)

小批量梯度下降算法是FG和SG的折中⽅案,在⼀定程度上兼顾了以上两种⽅法的优点。
每次从训练样本集上随机抽取⼀个小样本集， 在抽出来的小样本集上采用FG迭代更新权重。
被抽出的⼩样本集所含样本点的个数称为batch_size， 通常设置为2的幂次方， 更有利于GPU加速处理。
特别的， 若batch_size=1， 则变成了SG； 若batch_size=n， 则变成了FG.其迭代形式为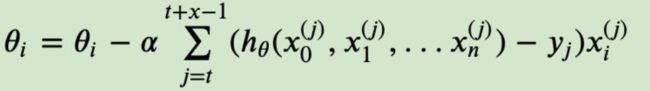

上式中， 也就是我们从m个样本中， 选择x个样本进行迭代(1

2.4 随机平均梯度下降算法(SAG)
 

在SG⽅法中， 虽然避开了运算成本⼤的问题， 但对于⼤数据训练而言， SG效果常不尽如⼈意， 因为每⼀轮梯度更新都完全与上⼀轮的数据和梯度⽆关。
随机平均梯度算法克服了这个问题， 在内存中为每⼀个样本都维护⼀个旧的梯度， 随机选择第i个样本来更新此样本的梯度， 其他样本的梯度保持不变， 然后求得所有梯度的平均值， 进而更新了参数。
如此， 每⼀轮更新仅需计算⼀个样本的梯度， 计算成本等同于SG， 但收敛速度快得多。
其迭代形式为：
 

• 我们知道sgd是当前权重减去步⻓乘以梯度， 得到新的权重。 sag中的a， 就是平均的意思， 具体说， 就是在第k步迭代的时候， 我考虑的这⼀步和前⾯n-1个梯度的平均值， 当前权重减去步⻓乘以最近n个梯度的平均值。
• n是⾃⼰设置的， 当n=1的时候， 就是普通的sgd。
• 这个想法⾮常的简单， 在随机中⼜增加了确定性， 类似于mini-batch sgd的作⽤， 但不同的是， sag⼜没有去计算更多的样本， 只是利⽤了之前计算出来的梯度， 所以每次迭代的计算成本远⼩于mini-batch sgd， 和sgd相当。 效果而言， sag相对于sgd， 收敛速度快了很多。 这⼀点下⾯的论⽂中有具体的描述和证明。
• SAG论文链接： https://arxiv.org/pdf/1309.2388.pdf

三、案列：波士顿房价预测

3.1 案列背景

数据介绍：

给定的这些特征， 是专家们得出的影响房价的结果属性。 我们此阶段不需要⾃⼰去探究特征是否有用， 只需要使用这些特征。 到后⾯量化很多特征需要我们自己去寻找

3.2 案列分析

回归当中的数据大小不⼀致， 是否会导致结果影响较⼤。 所以需要做标准化处理。

• 数据分割与标准化处理
• 回归预测
• 线性回归的算法效果评估

3.3 回归性能评估

均⽅误差(Mean Squared Error)MSE)评价机制：

注： y 为预测值， 为真实值
思考： MSE和最⼩⼆乘法的区别是？

• sklearn.metrics.mean_squared_error(y_true, y_pred)

    均⽅误差回归损失
    y_true:真实值
    y_pred:预测值
    return:浮点数结果

3.3 代码实现

 

# coding:utf-8

"""
# 1.获取数据
# 2.数据基本处理
# 2.1 分割数据
# 3.特征工程-标准化
# 4.机器学习-线性回归
# 5.模型评估
"""

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, RidgeCV, Ridge
from sklearn.metrics import mean_squared_error


def linear_model1():
    """
    线性回归:正规方程
    :return:
    """
    # 1.获取数据
    boston = load_boston()
    # print(boston)

    # 2.数据基本处理
    # 2.1 分割数据
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    print("正规方程:这个模型的偏置是:\n", estimator.intercept_)
    print("正规方程:这个模型的系数是:\n", estimator.coef_)

    # 5.模型评估
    # 5.1 预测值
    y_pre = estimator.predict(x_test)
    # print("预测值是:\n", y_pre)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差:\n", ret)


def linear_model2():
    """
    线性回归:梯度下降法
    :return:
    """
    # 1.获取数据
    boston = load_boston()
    # print(boston)

    # 2.数据基本处理
    # 2.1 分割数据
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归
    # estimator = SGDRegressor(max_iter=1000, learning_rate="constant", eta0=0.001)
    estimator = SGDRegressor(max_iter=1000)
    estimator.fit(x_train, y_train)

    print("梯度下降法:这个模型的偏置是:\n", estimator.intercept_)
    print("梯度下降法:这个模型的系数是:\n", estimator.coef_)

    # 5.模型评估
    # 5.1 预测值
    y_pre = estimator.predict(x_test)
    # print("预测值是:\n", y_pre)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差:\n", ret)


def linear_model3():
    """
    线性回归:岭回归
    :return:None
    """
    # 1.获取数据
    boston = load_boston()
    # print(boston)

    # 2.数据基本处理
    # 2.1 分割数据
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归
    # estimator = Ridge(alpha=1.0)
    estimator = RidgeCV(alphas=(0.001, 0.01, 0.1, 1, 10, 100))
    estimator.fit(x_train, y_train)

    print("岭回归:这个模型的偏置是:\n", estimator.intercept_)
    print("岭回归:这个模型的系数是:\n", estimator.coef_)

    # 5.模型评估
    # 5.1 预测值
    y_pre = estimator.predict(x_test)
    # print("预测值是:\n", y_pre)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差:\n", ret)


if __name__ == '__main__':
    linear_model1()
    linear_model2()
    linear_model3()

结果：

正规方程:这个模型的偏置是:
 22.6831683168
正规方程:这个模型的系数是:
 [-0.99452516  1.27554925  0.07762581  0.9043465  -2.23596893  2.19588662
  0.24084391 -3.32746498  2.58017729 -1.90390871 -2.1877224   0.67378414
 -4.0226854 ]
均方误差:
 24.458701657
梯度下降法:这个模型的偏置是:
 [ 22.81802616]
梯度下降法:这个模型的系数是:
 [-0.83544141  1.06010203 -0.0079003   0.67652484 -2.22253332  3.15715463
 -0.05974951 -3.09168393  1.93512922 -1.45236804 -2.0406664   0.73500676
 -3.46947672]
均方误差:
 20.7108504649
岭回归:这个模型的偏置是:
 22.6457920792
岭回归:这个模型的系数是:
 [-0.94813337  0.83436612  0.02132126  0.66582492 -1.77509715  2.78471829
  0.24597373 -2.32707713  2.05834176 -1.52598818 -2.26957139  0.71883795
 -3.57937585]
均方误差:
 26.1801660944

我们也可以尝试去修改学习率
 

estimator = SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.1)

此时我们可以通过调参数， 找到学习率效果更好的值。