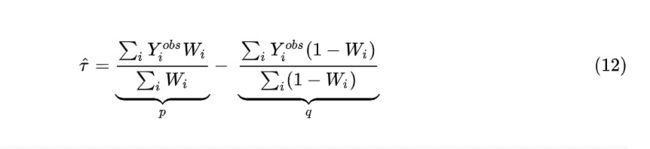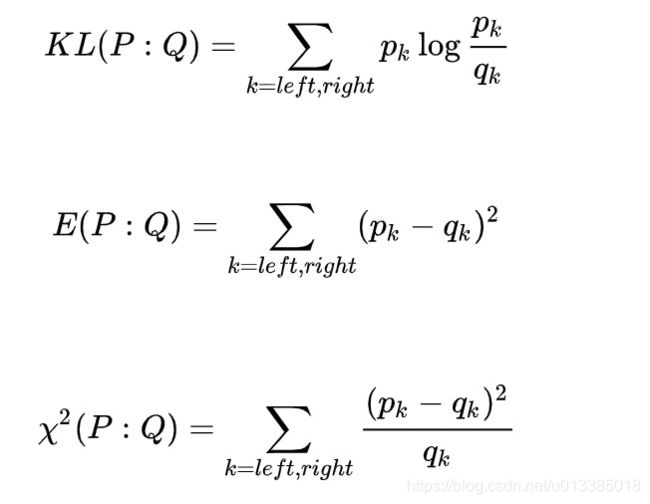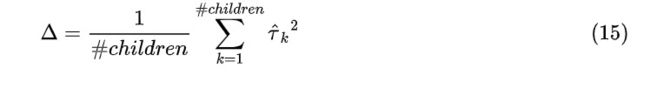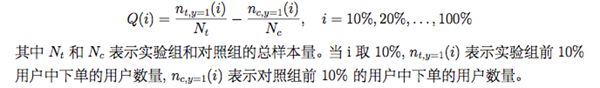营销:uplift模型
目录
一、uplift模型
1.1 间接建模
1.1.1 差分响应模型(Two-Model Approach)
1.1.2 差分响应模型升级版(One-Model Approach)
1.2 直接建模
二、Uplift Model 模型评估
2.1 Qini curve
2.2 AUUC
三、分发策略
3.1 贪心分配
3.2 整数规划
参考文献
四、营销迭代计划
五、代码
六、参考文献
一直以来机器学习希望解决的一个问题就是'what if',也就是决策指导:
- 如果我给用户发优惠券用户会留下来么?
- 如果患者服了这个药血压会降低么?
- 如果APP增加这个功能会增加用户的使用时长么?
- 如果实施这个货币政策对有效提振经济么?
这类问题之所以难以解决是因为ground truth在现实中是观测不到的,一个已经服了药的患者血压降低但我们无从知道在同一时刻如果他没有服药血压是不是也会降低。
这个时候做分析的同学应该会说我们做AB实验!我们估计整体差异,显著就是有效,不显著就是无效。但我们能做的只有这些么?
当然不是!因为每个个体都是不同的!整体无效不意味着局部群体无效!
- 如果只有5%的用户对发优惠券敏感,我们能只触达这些用户么?或者不同用户对优惠券敏感的阈值不同,如何通过调整优惠券的阈值吸引更多的用户?
- 如果降压药只对有特殊症状的患者有效,我们该如何找到这些患者?
- APP的新功能部分用户不喜欢,部分用户很喜欢,我能通过比较这些用户的差异找到改进这个新功能的方向么?
以下方法从不同的角度尝试解决这个问题,但基本思路是一致的:我们无法观测到每个用户的treatment effect,但我们可以找到一群相似用户来估计实验对他们的影响。
一些概念
ATE 和 CATE
Casual Inference 目前主要集中在如何估计 CATE. 由于不可能同时观察到对于一个个体施加与不施加 Treat 的 结果. 因此这个任务和传统的预测任务所采用的方法有较大的区别.
我们会围绕以下的方法, 慢慢描述因果推理这个领域的发展, 这些方法先贴出来.
一、uplift模型
- 最显然的方法是建立两个模型(two-model),一个模型训练treatment ,另外一个模型训练control数据。使用时我们将两个模型的预测值进行相减作为最终的结果。这里有个主要的缺点:我们想要的概率预测值可能与单独每一个模型差异很大(我们想要预测是实验组和对照组的差异,而模型训练目标只是各自的数据组内把正负样本分开,并不能学到两种组的差异情况)。在决策树的情况下,它并不一定有利于因为action而导致的实验组和对照组的相应差别分裂,而是在实验组和对照组各自的组内预把预测结果分开。
- 训练一个模型,试图直接为实验组和对照组的差异进行建模
1.1 间接建模
两个模型的差分模型,标签转化无倾向性得分模型,代码如下
https://github.com/PGuti/Uplift
1.1.1 差分响应模型(Two-Model Approach)
差分响应模型很直觉。分别对AB实验的实验组和对照组数据独立建模,预测时分别实验组模型和对照组模型预测用户的分数,两个模型预测分数相减就得到了uplift score
以优惠券发放为例,目标是用户是否下单。训练时取实验组的用户训练,正样本是下单用户,负样本是未下单用户,预测结果是每个用户下单的概率。类似地,对照组也可以使用另一个模型预测出每个用户下单的概率
预测时,对用户分别使用实验组和对照组两个模型进行预测,两个模型预测的分数相减即得到预测用户upliftscore,最后根据upliftscore高低决定是否发券。
1.1.2 差分响应模型升级版(One-Model Approach)
差分响应模型的训练数据和模型都是各自独立的,可以分别在训练数据层面上打通以及在模型层面上打通,得到升级版的差分响应模型。
- 无标签转化+引入干预相关特征
在实验组和对照组的用户特征中,加入与T(干预)有关的特征,实现数据层面的打通,即实验组和对照组合并,使用同一个模型训练。这是阿里文娱提到的一种方法,但我感觉这样无法满足用户特征样与条件策略独立的假设
2. 标签转化
3. 标签转化+引入个人倾向性得分
在模型选择上,我们以XGBoost模型作为基学习器,分别在Two Model差分响应模型、One Model差分响应模型(无标签转化+引入T/C特征)、One Model差分响应模型(引入标签转化)和One Model差分响应模型(引入个人倾向分)上进行了尝试。
Two Model模型会导致误差累计,在具体实验中也得到了同样结论;标签转化方法在逻辑上推导可行,实验结果显示并不尽如人意,分析其主要原因还是对于样本的要求太高,目前构造的数据虽然保证了实验组和对照组用户数量基本一致,但是完全随机基本无法保证。相反,引入个人倾向分后,将其转化为回归问题,在一定程度上解决了这个问题,标签转化虽然逻辑上可以,但是还是需要一定解释成本。
在实验中表现最好的One Model差分响应模型(无标签转化+引入T/C特征),在结果输出上解释成本也是最低的,在对于每个用户预测时,分别加入T和C干预信号特征,然后预测值相减即得到用户的uplift score。
1.2 直接建模
这种方式是修改现在已有的学习器结构进行直接对uplift建模。有修改LR、k-nearest neighbors、SVM,比较流行的还是修改树学习器。在这个章节中主要介绍的是基于树的方法,并讨论树的分裂标准。 这里我们定义是随机时间,即对任意特征倾向得分,评估ATE的效果为:
简单的讲,公式12就是用treatment的平均结果减去control的平均结果,p和q分别表示也是如此
第一种分裂标准是求两个叶子节点的区别:
分别在左右叶子节点上用公式12求出和
Rzepakowski and Jaroszewicz基于信息论提出另外一种分裂标准:
这里是差异度量,、分别是treatment组合control组的概率分布。因此,这个分裂的表示是分裂后的发散增益程度。对于有以下三种方式Kullback, Euclidean、Chi-Squared:
在因果树模型中,Athey and Imbens提出以下分裂标准:
可以发现,当二分类结果时,公式15等价于上述的欧式分裂标准方式 。
值得注意的事,Athey and Imbens提出一种“诚实”的方法,没有使用相同的数据进行生成树并估计叶子之间的uplift。而是把数据分为两部分,一部分用于生成树结果,另外一部分用于估算叶子节点的uplift值。
KL散度:两个分布之前的差异
https://mp.weixin.qq.com/s/BwOQw-CK-d0C-cOIHjooSA
二、Uplift Model 模型评估
有哪些方法可以进行异质性因果推断?
目前比较流行的一些方法,诸如回归树 (Breiman, Friedman, Olshen, and Stone,1984)、随机森林(Wager and Athey,2018)、LASSO (Tibshirani, 1996),还有就是支持向量机 (Vapnik, 1998,2010)等。
ATE(Average treatment effect),ITE(Individual treatment effect),CATE(Conditional Average treatment effect)区别?
ATE=E[Y(1)]-E[Y(0)]
ITE=Yi(1)-Yi(0)
CATE=E[Yi(1)-Yi(0)|Xi=x]
我们从公式也大致能够看出,ATE,ITE和CATE区别在哪里。
Rubin的因果模型得出的是ATE,即接受和不接受某种处理的平均因果效应。
随着我们可以收集的个体特征的数量变多,我们对于每个个体的了解也变得更加的细致,因此现在有很多研究者开始关注ITE即个体处理效应,这个在生活中有很大的运用价值。它能够帮助政策制定者更好的根据每个地区、甚至每个人选取不同的诊疗方案。
然而,没有一些很强的假设,个体的因果效应通常是难以识别的,因为同分布的观测数据背后可能对应的是不同的数据生成过程,进而个体的因果效应也可能是不同的。
但CATE,特征变量取值为x的条件下处理效应的大小。这个相比ITE的识别难度会更能够接受。在最小化均方误差的条件下,寻找个体处理效应的估计量与寻找与之对应的条件平均处理效应的估计量是等价的。而CATE就是用来分析异质性的。
常用分类和回归算法,可以通过 AUC、准确率和 RMSE 等去评估模型的好坏。而由于 Uplift Model 中不可能同时观察到同一用户在不同干预策略下的响应,即无法获取用户真实增量, 我们也就无法直接利用上述评价指标去衡量模型的好坏。因此,Uplift Model 通常都是 通过划分十分位数来对齐实验组和对照组数据,去进行间接评估。 常用的评估方 法有 Qini 曲线、AUUC 等。
Qini 曲线是衡量 Uplift Model 精度方法之一,通过计算曲线下的面积,类似 AUC 来评价模型的好坏。其计算流程如下
(1) 在测试集上,将实验组和对照组分别按照模型预测出的增量由高到底排序,根据用户数量占实验组和对照组用户数量的比例,将实验组和对照组分别划分为十份,分别是 Top10%, 20%, . . . , 100%。
(2) 计算 Top10%,20%,…,100% 的 Qini 系数,生成 Qini 曲线数据 (Top10%,Q(Top10%)),(…,…), (Top100%, Q(Top100%))。Qini 系数定义如下:
可以看出,Qini 系数分母是实验组和对照组的总样本量,如果实验组和对照组用户数量差别比较大,结果将变得不可靠。
2.1 Qini curve
Qini 曲线是衡量 Uplift Model 精度方法之一,通过计算曲线下的面积,类似 AUC 来评价模型的好坏。其计算流程如下
(1) 在测试集上,将实验组和对照组分别按照模型预测出的增量由高到底排序,根据用户数量占实验组和对照组用户数量的比例,将实验组和对照组分别划分为十份,分别是 Top10%, 20%, . . . , 100%。
(2) 计算 Top10%,20%,…,100% 的 Qini 系数,生成 Qini 曲线数据 (Top10%,Q(Top10%)),(…,…), (Top100%, Q(Top100%))。Qini 系数定义如下:
可以看出,Qini 系数分母是实验组和对照组的总样本量,如果实验组和对照组用户数量差别比较大,结果将变得不可靠。
2.2 AUUC
AUUC(Area Under the Uplift Curve) 的计算流程与 Qini 曲线的计算流程一样,计算前 10%、20%、. . . 、100% 的指标,绘制曲线,然后求曲线下的面积,衡量模型的好坏。不同是 AUUC 指标计算方法与 Qini 指标计算不同,AUUC 指标定义如下:
与 Qini 指标含义相同,当 i 取 10% 时,nt(i)nt(i) 表示实验组前 10% 用户数量,nc(i)nc(i) 表示对照组前 10% 用户数量。 可以看出,AUUC 指标计算方法可以避免实验组和对照组用户数量差别较大导致的指标不可靠问题。
值得注意的是,当分桶时,对照组边界点预估出的增量与实验组边界点的预估值有较大差别时候,以上的两个评估指标似乎都显得不那么可靠了。 因此在实际中,我们使用的往往是 AUUC 另外的一种计算方法。
AUUC 是一个很重要且奇怪的指标。说重要,是因为它几乎是 Uplift Model 在离线阶段唯一一个直观的,可解释的评估模型优劣的指标。说奇怪,是因为它虽然本质上似乎借鉴了分类模型评价指标 AUC 的一些思想,但是习惯了 AUC 的算法工程师们在初次接触的时候一定会被它搞得有点迷糊。
作为在分类模型评估上的标杆,AUC 的优秀不用过多赘述。其中最优秀的一点是它的评价结果稳定到可以超越模型和样本本身而成立,只要是分类问题,AUC0.5 是随机线,0.6 的模型还需要迭代一下找找提升的空间,0.6-0.8 是模型上线的标准,而 0.9 以上的模型就需要考虑一下模型是否过拟合和是否有未知强相关特征参与了模型训练。 一法抵万法,我们可以抛开特征,样本和模型构建的细节而直接套用这套准则。
然而这个特点对于 AUUC 就完全是奢望了。通过 AUUC 的公式可以看出,AUUC 最终形成的指标的绝对值大小是取决于样本的大小的。也就是说,在一套测试样本上,我们的 AUUC 可能是 0 到 1W,而换了一套样本,这个值可能就变成了 0 到 100W。这使得不同测试样本之间模型的评估变为了不可能。也使得每次模型离线的迭代的前提必须是所有模型都使用同一套测试样本。当我们训练完一个新的模型,跑出一个 40 万的 auuc,我们完全无从得知这个值背后代表着模型精度如何,我们只能拿出旧的模型在同样测试集上跑出 auuc 然后相互比较。这无疑让整个训练迭代过程变得更痛苦了一点。
我们也尝试了从多个角度去解决这个问题,希望在增量预估模型中建立一套类似 auc 的标准,但无一例外都没能成功。包括像 AUC 那样除以曲线的理论最大面积,但是看公式就可以知道,这个理论的最大面积其实就是样本个数的平方而这么一除之后得到的 AUUC 也失去了比较的价值了。
我们还尝试过使用 AUC 的近似计算方法(Pairwise)去近似计算 AUUC,得到的结果虽然确保了在 0-1 区间内的离散性但仍然无法保证在所有情况下,他得出的模型优劣顺序与 AUUC 本身保持一致。
最后,我们也只能用“补贴问题本身就是与实验批次和样本强相关的问题”这个理由盖过对这个问题的纠结。但 能否在增量预估模型中建立一套类似 auc 的标准 ,我们仍然认为这个问题是值得投入一点心力去探索的方向。
三、分发策略
对增量预估完毕后,接下来就需要具体地为用户池中用户分配补贴券。在基于增量预估的基础上,我们尝试了两种分发策略:
3.1 贪心分配
很多时候,运营对于使用的券类别和每个券类别的预算分配都有 比较大的限制和约束 。在这样的约束下,我们的做法是按照券值面额从低到高,为每个券类别计算可支配数量,然后对用户池所有用户按照预估出的 Uplift 值和计算出的可发放数量倒排截断,并将分配完毕的用户从备选用户池中移除。这样一个用户如果在 各种券类别下 uplift 都很高时,我们将会优先为他/她配置券值较低的补贴券 。这样做法的好处是简洁明了实现简单,在人工干预较强的时候对于运营的可解释性也比较强。缺点当然就是在自由度更高情况下,显然不能达到全局最优。
3.2 整数规划
参考文献
python运筹优化(一):Cplex for python使用简介 最多支持1000个参数
遗传算法做整数规划(0-1优化)Python实现
四、营销迭代计划
1. 对人群的圈选(是否发券)建模
2. 对券面额的建模
3. 对券权益的建模
4. 不同券之间的相互影响建模
多任务建模
5. 长期营销下用户心智的变化
五、代码
https://github.com/uber/causalml
https://github.com/df-foundation/pylift
六、参考文献
智能营销增益模型(Uplift Modeling)的原理与实践
https://blog.csdn.net/jinping_shi/article/details/105583375
Decision trees for uplift modeling 论文笔记
https://zhuanlan.zhihu.com/p/194273622?utm_source=wechat_session
DiDi Food中的智能补贴实战漫谈
https://www.infoq.cn/article/mpkjAbSW9mwmy5AdArhM
详解阿里文娱智能影响模型
http://mudu.tv/live/watch/technology?id=vljbea5m
Causal Inference and Uplift Modeling A review of the literature论文笔记
https://zhuanlan.zhihu.com/p/192960265
Uplift-Model在贝壳业务场景中的实践
https://mp.weixin.qq.com/s/h1Aiy6wpZBrsCwLLTny8dQ