FaissPQ索引简介

1.向量检索问题

随着神经网络的发展，embedding的思想被广泛的应用在搜推广、图像、自然语言处理等领域，在实际的工业场景中，我们常常会遇到基于embedding进行文本、图像、视频等物料的相关内容检索问题，这类问题通常要求在几毫秒的时间内完成百万甚至亿级别候选物料上的检索。
在这类问题中，主要需要考虑的三个问题是速度、内存以及准确性，其中速度是必须要解决的问题，同时我们希望能在保证速度的基础上，尽可能的提升准确率，降低内存占用。因此可以想到，我们是不是可以通过一定的方法，利用内存和准确率来换取查询速度的提升。
Faiss是由FacebookAI团队开发的向量检索库，提供了多种向量查询方案，可以实现在亿级别候选物料上的毫秒级查询，是目前最主流的向量检索库。在Faiss中，把具体的查询算法实现称为索引，由于faiss中提供了多种类型的索引，因此了解其中不同索引索引的实现方式对于我们的应用就尤为关键。

2.faiss索引类型

)

faiss索引类型主要可以分为暴力检索、乘积量化、局部敏感哈希、基于图的方法。
向量检索问题通常需要考虑召回率、耗时以及内存占用三个问题，而实际的工业场景中，一般存在候选物料量级较大，耗时要求高的情况。
对比faiss的索引类型，暴力检索类索引虽然召回率百分百，但耗时无法接受。而常用的索引类型主要是乘积量化和图两类标签。
其中，基于图的方法召回率可以逼近暴力检索且耗时也略优于乘积量化类索引，但是在构建索引过程中需要占用的内存很大，如果能保证足够的资源，图方法可以在耗时和召回率上做到最优。
乘积量化召回率低于图方法，但是能保证较好的耗时和空间占用，是在候选物料集较大时的最优选择。

索引	召回率	耗时
暴力检索	最优	最差
基于图的索引	优	优
乘积量化	次优	优

3.乘积量化

3.1 向量量化

在介绍乘积量化前，首先需要介绍向量量化的基本概念。
向量量化和信号编码的概念基本类似，就是将由连续值构成的向量$x$从欧式空间映射到一个由有限离散值构成的集合$C=c_i,i\in [1,l]$中,定义该映射为$q$,则$q(x)\in C$,这里$C$也成为codebook。

如上图所示，定义映射函数$q$为kmeans，向量量化流程如下:

1.训练kmeans聚类，得到每个点所属的聚类编号
2.将每个向量所属的聚类编号作为量化结果

faiss中对应该类方法的索引类型为IndexIVFFlat。

3.2 乘积量化

乘积量化的思路就是将向量分割成多段后，对每一段分别进行向量量化。
假设将向量维度为$D$,切分成$m$段，则每段的维度大小为$D^{\ast }=D/m$，对于第$i$个分段，向量表示为$[x_1^i,x_1^i,...,x_{D^{\ast }}^i]$,对应的codebook为$C_i$。
在索引训练完成后，全局的codebook表示为各个分段量化结果的乘积$C=C_1\ast C_2\ast ...\ast C_m$，这也是乘积量化的命名原因。

3.3 空间占用对比

假设向量维度为D,向量量化的codebook大小为$k$,存储codebook需要$kD$的空间;乘积量化每个分段只需要$k^{\ast }$的codebook大小,存储codebook需要$k^{\ast }D$的空间。可以发现，分段量化后可以在空间占用更小的情况下达到一样大的codebook规模。

3.4 faiss中乘积量化的应用

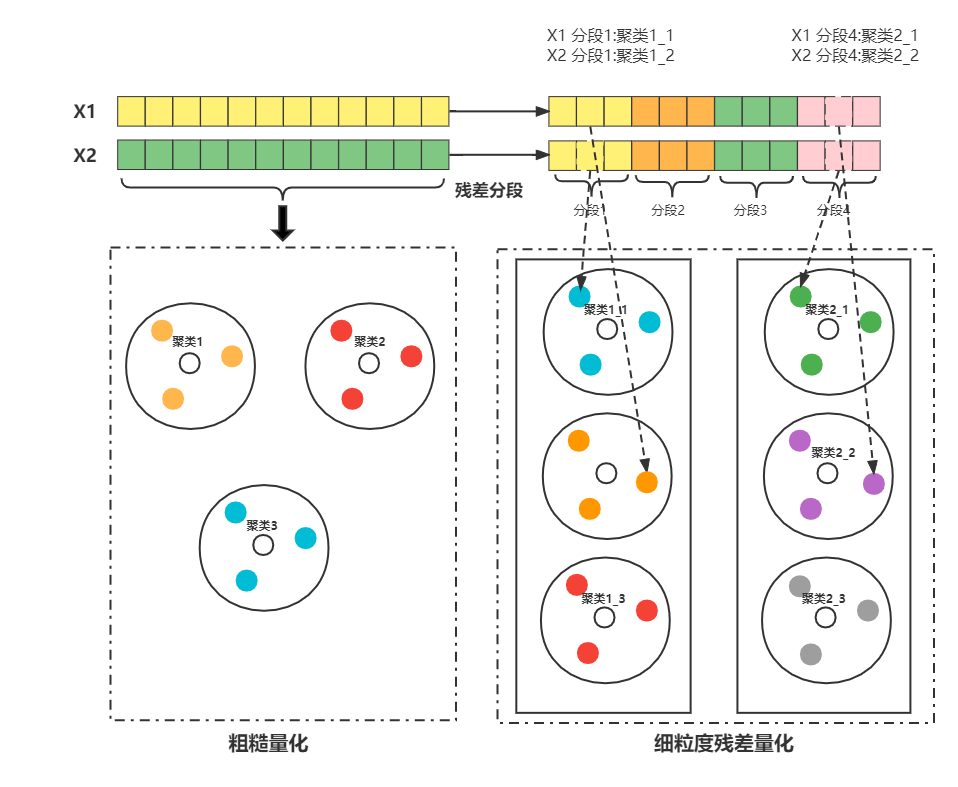
在faiss的乘积量化的实现中，还引入了层次化量化的思想，在乘积量化前引入了一层粗糙量化，形成粗糙量化+细粒度量化的两层结构。引入粗糙量化的主要目的在于优化查询速度，由于候选向量的数量级一般较大，如果直接遍历所有候选，效率还是很难达到要求。加入粗糙量化后，通过计算查询向量到粗糙量化类簇中心的聚类就可以选出几个最有可能包含正确结果的类簇，然后再在这些类簇上进行第二级的查询，就可以大大缩减查询时间，同时保证查询效率
索引构建:
1. 构建第一层的量化器$q_c$,codebook $C_c$,得到每个向量X的向量量化结果$x_c=q_c(x)$
2. 计算每个向量粗糙量化后的残差$x_r=x-x_c$,对$x_r$进行乘积量化

粗糙量化+细粒度量化的形式可以进一步加快查询速度，但是也会造成一定的召回率损失，实际应用时需要通过调参较低这一影响。
在粗糙聚类后，各个类簇内的向量分布可能差异较大，如果直接用原始向量进行细粒度量化，可能在检索时会放大误差，使用残差进行细粒度量化能缓解这个问题。

向量查询
在两层量化构建索引后，查询可以改写为如下形式
$$d(x,y)=d(y,x_c+x_r)=||y-x_c|{|}^2+||x_r|{|}^2+2x_c{x}_r-2y{x}_r$$
其中,$||x_r|{|}^2+2x_c{x}_r$和y无关，可以预先计算缓存，$||y-x_c|{|}^2$部分需要计算查询向量$y$到粗糙聚类中心的距离，这部分的计算量取决于训练时设定的粗糙聚类中心个数，$2y{x}_r$部分需要计算查询向量和簇内残差向量，这部分计算量和设定的查询类簇数量相关，最坏情况下需要遍历所有类簇。

3.5 超参

构建PQ索引时，超参数的选择会在很大程度上影响线上效果，需要多调参找到召回率和耗时之间的trader-off。
主要影响效果的参数包括粗糙量化类簇个数、分块数量、分块字节等影响索引训练的参数，查询的类簇数量这种影响查询阶段的参数，除此之外PQ索引类型对查询效果也有很大影响，可以尝试PQ，OPQ，PQ with PCA等不同索引。

4.参考资料

1. Huang J T , Sharma A , Sun S , et al. Embedding-based Retrieval in Facebook Search[C]// 2020.
2. faiss wiki:https://github.com/facebookresearch/faiss/wiki
3. 语义向量召回之ANN检索:https://mp.weixin.qq.com/s/YOnzPcQiaoNf1aSImNOA5g
4. Faiss基于PQ的倒排索引实现:https://zhuanlan.zhihu.com/p/34363377

转转研发中心及业界小伙伴们的技术学习交流平台，定期分享一线的实战经验及业界前沿的技术话题。
关注公众号「转转技术」（综合性）、「大转转FE」（专注于FE）、「转转QA」（专注于QA），更多干货实践，欢迎交流分享~