知识图谱从入门到应用——知识图谱推理：基础知识

分类目录：《知识图谱从入门到应用》总目录

---

推理能力（Reasoning）是人类心智区别于普通物种的重要特征之一。人类通过推理，从已知的事实中获取和习得新的知识，包含了认知、理解、抽象、演绎、归纳、溯因、类比等多种不同形式的推理思维过程。利用机器实现类似于人类心智的推理能力是人工智能自诞生以来最核心的目标和任务之一。构建各种各样的知识图谱来描述客观世界，抽象万物之间的逻辑关系，不只是为了查询和搜索关于万物的信息，更是为了能够基于这些关于事物的描述性事实，去推断、归纳和预测未知的事实。因此，推理是知识图谱最为关键的技术。知识图谱与人工智能在这个方面的关系主要体现在两个方面：一个是从知识表示的维度，即：怎样表示和描述知识，进而完成推理；二是从知识表示学习的角度，希望基于表示学习和神经网络来完成知识推理。这两个方面刚好对应在知识图谱上完成推理的两种不同方法基于符号逻辑的推理和基于表示学习的推理。需要特别指出的是，这两种推理实现形式对于知识图谱的推理应用是同等重要的，会在本章中具体分析这两种技术手段的优缺点，以及集成两者的一些方法。

什么是推理

首先来回答一个问题：什么是推理？随着人工智能的复兴，推理也经常被人们提及。推理和逻辑是密切相关的，关于推理的研究更多和更早地出现于哲学和数学领域。古希腊有个词叫Logos，指世界的可理解的一切规律，涉及逻辑描述语言、逻辑思维方式、逻辑推理过程等内容。当然，我们并不希望陷入关于推理的哲学思辨中，所以在本文中还是更多地从人工智能发展历史上出现的关于推理的研究来展开探讨。即使是在人工智能领域，有关推理的研究也非常广泛和深入，区别于一般意义上的机器推理研究，在这里也仅仅局限于那些与知识图谱密切相关的一些推理方法来探讨推理的问题。简而言之，推理指的是从已知事实（Known Facts）来推断得出新的事实（New Facts）的过程。有很多种实现推理的方法，较为常见的有演绎、归纳、溯因、类比，如下图所示：

首先来看演绎推理（Deductive Reasoning）。演绎推理是一种Top-down Logic，在日常思维过程中经常被用到。例如肯定前件（Modus Ponens）推理逻辑十分简单：假设知道$P$能推出$Q$，如：“如果今天是周四，张三就会去上班”，同时也知道$P$的事实，如“今天正好是周四”，就可以推理得出$Q$，即“张三会去上班”。另外一种否定后件（Modus Tollens）推理也很简单：同样假设知道$P$能推出$Q$，如：“如果下雨，天空肯定有云”，同时知道否定的$Q$，即“天空没有云”，就可以推理得出否定的$P$，即“没有下雨”。再比如三段论推理逻辑：假设知道$P$能推出$Q$，$Q$能推出$R$，那么$P$也可以推出$R$。

第二类常见的推理称为归纳推理（Inductive Reasoning）。和演绎推理不一样，归纳推理是一种Bottom-up Logic，指的是通过观察客观事实进而总结和归纳抽象知识的推理过程。例如，假如观察发现看到的天鹅都是白色的，于是可能归纳得出所有的天鹅都是白色的。显然归纳推理不一定是正确的，因为突然发现还有黑色的天鹅存在。实际上，日常生活中的推理都是这种近似正确的推理，尽管不一定百分百正确，但很有用。再看两个归纳逻辑的例子，假设箱子中有很多白色或黑色的球，随机地从中取出一部分球，发现其中$\frac{3}{4}$是黑色，$\frac{1}{4}$是白色的，于是可以近似得出整个箱子中的球黑色占比$\frac{3}{4}$。再比如，统计发现90%就读某高中的学生都会上大学，如果张三是该高中的学生，就会归纳推断他极大可能也会上大学。

还有一种很有用的推理形式称为溯因推理（Abductive Reasoning）。现在谈论深度学习的缺点，经常会说到一个问题即可解释的问题。溯因推理关注的一个方面就是推理结果的可解释逻辑。下面举例说明，假如知道一个假设或规则：“如果下雨，草地就会湿”，现在观察到草地已经湿了，基于已知假设，我们推断得出：“可能是下雨导致的潮湿”。所以，首先溯因推理也是一种从观察现象出发的推理，但和归纳推理不同，它是将抽象的规则知识与观察现象相结合，寻找可能原因的推理的过程。而归纳推理则是从观察到的现象和原因出发，归纳抽象规则的过程。当然和演绎推理更加不同，演绎推理是将抽象规则知识与原因相结合，推理得出结果的过程。

还有一类在传统人工智能领域被研究得比较多的推理称为类比推理。人们经常采用类比思维来解决问题，特别是在学习样本很少的情况下，习惯于寻找类似的解决方案来解决面临的新问题。例如，假如我已经学过草莓饼干怎么做，现在需要做菠萝饼干，就会去比较两者的相同和不同之处。抽象来讲，类比推理的过程是：假设$P$和$Q$在某些属性上相似，如$a$、$b$、$c$，同时观察到$P$有一个新属性$x$，因此，可能类比推理得出$Q$也可能具有$x$属性。和归纳推理不同，类比推理从个体到个体的推理过程。本质上，在机器学习领域的迁移学习也属于一种类型的类比推理过程。

机器推理举例

基于描述逻辑的推理

首先看一个和知识图谱有密切关系的利用描述逻辑实现机器推理的例子。顾名思义，描述逻辑关注的是描述客观世界的逻辑，也就是本体（Ontology）。本体指的是大脑中关于世界的描述模型。通常一个本体知识库包含TBox用来存储抽象概念，ABox用来存储事实性描述。这就好比我们来到这个世界，首先记住的是万事万物的名称，然后会基于这些名称进一步抽象概念，如人分为男性、女性，生物分为动物和植物等。我们还会利用抽象的概念和事实描述来进行推理。如下图所示，定义Father的概念是指有小孩的男性，还定义了一个HappyFather的概念指那些小孩是医生或律师的父亲。假如在ABox中有一个事实描述John是HappyFather，同时还知道Mary是John的小孩，基于TBox中的关于HappyFather的定义，可以推理得出Mary可能是医生或者律师。这是一种严格的符号逻辑推理。假如可以非常精确地用这种符号表示复制人脑中的本体描述和所有事实性描述，就可以利用机器模拟人脑完成这类推理。但符号表示是有局限性的，关于这一点，将在后面的文章专门谈到。

自然语言推理

人类的自然语言也可以描述世界万物，包括概念、事实和逻辑规则等。既然人可以利用自然语言实现推理，当然也希望机器能模仿人的语言实现自动推理。因此在自然语言处理领域，也有一个任务与推理有关，称为自然语言推理（Natural Language Inference，NLI）。NLI的任务定义比较简单：给定两句话，要求机器能判断它们之间是否是蕴含或冲突关系。例如：句子“他正在打鼾”蕴含了“他正在睡觉”。自然语言的缺点是没有描述逻辑那样严格的形式化逻辑定义，但优势是语料数据更加容易获得。

视觉推理

在计算机视觉领域也有不少和推理相关的任务。例如CLEVR数据集定义了一系列视觉推理（Visual Reasoning）的问句。如下图所示，给定一张图片，视觉推理不仅要求识别其中的物体，还需要分析它们之间的位置关系、实现路径搜索、比较属性大小和计数等。严格地说，这些问句还不是逻辑型的问句，但也是基于视觉识别进一步实现复杂逻辑推理的基础。

表示与推理

在计算机领域还有很多关于机器推理的研究，但不论哪种推理的实现，其本质都是要找到一种合适的表示方法，一方面这种表示能方便而且准确地刻画客观世界中的事物以及运行规律，另外一方面，这种表示又非常适合于机器处理和计算。可以将其称为面向机器的知识表示。在后面的介绍中，我们将会看到符号表示和向量表示是当前实现知识图谱推理的最常用的两种机器表示方法。

知识图谱上的推理实现

总的来说，在知识图谱上可以实现演绎、归纳、溯因和类比等各种形式的推理。同时，深度学习的出现又为利用神经网络和表示学习方法实现推理提供了新的技术手段。因此，后面也会着重关注综合利用知识图谱和神经网络实现推理的新方法。推理的实现和应用都是比较困难的。知识图谱将推理任务进行了简化，并将推理任务限定为基于图结构完成关系推理和事实预测。知识图谱中的每一条三元组都代表关于客观世界的一条事实描述，同时图的结构又进一步为推理提供了关联线索。简而言之，知识图谱推理的目标是利用图谱中已经存在的关联关系或事实来推断未知的关系或事实，很多现实的问题如推荐计算、因果分析、查询问答和实体对齐等任务都可以归结为实体之间的关系推理问题。如下图所示，推理可以用于属性补全、关系预测、错误检测、问句扩展和语义理解等。在查询和问答中，推理可以用来拓展问句语义和提高查询召回率。在推荐计算中，推理可用来提升推荐的精准性和可解释性。此外，推理在深度语言语义理解和视觉问答中也扮演必不可少的角色。凡是包含深度语义理解的任务都会涉及推理的过程。

有很多种在知识图谱上实现推理的方法，这里将较为常见的方法按表示方法和推理模式两个维度进行了分类，如下图所示。前文已经提到，符号表示是一种显式的知识表示方法，它的最大优势是可解释性很好。而向量表示的优势是比较易于捕获隐含的知识，例如可以利用两个实体在向量空间的位置推算它们可能存在的各种关系。这很重要，因为永远无法显式描述所有的知识。但向量表示的最大缺点是丢失了符号表示的可解释性。参数化的数值对机器是友好的，但不利于人来理解。从推理模式的维度，主要从演绎推理和归纳推理两个维度进行划分。演绎推理更多依赖于显式的知识描述和逻辑推导，而归纳推理则更多地依赖于大数据和机器学习方法。

在本文中，将分别介绍基于符号表示的演绎推理方法，如利用本体公理或Datalog实现的推理；基于符号表示的归纳推理，如利用图结构做归纳的路径排序算法（Path Ranking Algorithm，PRA）和利用规则归纳学习的关联规则挖掘（Association Rule Mining under Incomplete Evidence，AMIE）。进一步会重点介绍当下更为流行的基于表示学习和神经网络的知识图谱推理方法，例如知识图谱嵌入系列模型和基于图神经网络图谱推理模型等。还有一类方法研究基于向量表示学习符号规则，再利用符号规则做演绎推理，这实际上是一类将基于符号的演绎推理和基于向量的归纳推理相结合的方法，也是当前人工智能和知识图谱的一个研究热点。当然，也可以基于知识图谱完成溯因推理、类比推理和因果推理等其他推理模式。

基于本体公理的知识图谱推理

前文已经介绍过，一个定义得比较好的知识图谱包含TBox，即Schema层，主要定义概念以及关系；同时还包含ABox，包含事实性断言或描述，如下图所示。在TBox中，可以定义很多本体公理（Ontological Axioms）用于实现演绎推理。这种基于本体公理的演绎推理是一种基于符号表示的演绎推理方法。还有很多其他在知识图谱上实现的符号演绎推理方法，例如基于Datalog的推理等，将在后面的文章中展开介绍。

可以为一个知识图谱定义很多公理，例如，定义一条代表类别之间包含关系的公理：“人工智能公司rdfs:subClassOf高科技公司”，或者定义一条领域公理，声明投资关系的“domain”是投资人。利用这些简单的公理就可以实现一些简单的演绎推理了。比如，如果知道谷歌是一家人工智能公司，就可以应用第一条公理推理得出谷歌也是一家高科技公司。这种基于符号本体实现的演绎推理一个特点是很精确，并且不存在可解释的问题，因为每一个推理得出的结论都可以回溯和给出推理的过程。基于本体公理的推理也可以非常复杂。在描述逻辑领域，数十年的努力都在研究怎样用符号逻辑来表示各种各样的本体公理，同时研究这些公理组合所对应的推理是否完备，是否可以计算，计算的复杂度又是多少。例如，可以为关系定义更细致的语义。通过传递属性公理（Transitive Property Axiom），可以声明某个关系如ancester是传递关系。通过inversof axiom可以声明两个关系（如ancestor和descendant）是互反关系。有了这些公理，就可以进一步完成更为复杂的演绎推理。

基于图结构与规则学习的知识图谱推理

也可以基于符号表示在知识图谱上实现归纳推理。例如，PRA就是一种利用知识图谱的图结构信息实现归纳推理的算法。它的基本假设是：两个实体之间所有可能的路径都可能作为推断两个实体存在某种关系的线索或依据。如下图所示，希望推断Charlotte的职业是否是Writer，可以从Charlotte出发找出所有能抵达Writer的路径。例如，发现她的父亲是Patrick，而Patrick的职业是Writer。这当然可以作为证明Charlotte也是作家的一条可能依据。PRA对这些可能的路径进行排序加权，推断待预测关系的概率。

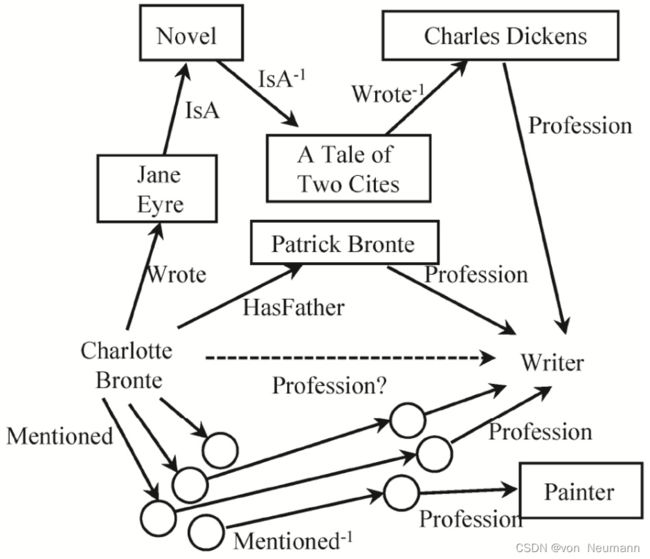
可以对整个图谱进行统计学习，如果训练数据足够多，期望能统计出这类规律或规则，例如：可能统计出很多父亲是作家的人也可能是作家。当然，这肯定只是一种近似推断，但和基于公理的演绎推理相比，PRA不需要人工定义规则，并能充分利用大数据和机器学习进行归纳推理。同时，显式的路径特征也可以直接用于对推理的结果进行解释，因而也不存在可解释的困难。类似的知识归纳模型AMIE等也是利用知识图谱已经存在的事实和图结构学习出一组规则，再利用规则完成推理。但这类方法有一个缺点是依赖于对整个知识图谱做搜索匹配，在知识图谱规模增大的情况下，搜索空间和复杂度也急剧上升，学习的效率也会随之降低。

基于表示学习的知识图谱推理

深度学习和表示学习的兴起启发了人们研究基于向量表示的推理方法。例如，TransE和DistMul等知识图谱嵌入系列模型。这些模型的基本思想是将知识图谱中的实体和关系都投影到向量空间。如下图所示，可以将Rome、Paris等实体，以及is-capital-of关系都投影到向量空间，再通过向量空间完成推理计算。这些模型通常以知识图谱的三元组为训练输入，通过定义一个约束函数对向量表示进行学习。

例如，DistMult模型定义了一个向量乘法函数，要求：如果两个实体$h$、$t$之间存在$r$关系，那么，$h$的向量乘以代表$r$关系的矩阵$Mr$所得出的向量应该在向量空间与$t$比较接近。这些向量或矩阵就称为实体和关系的嵌入（Embedding）。向量表示的一个优势是推理的计算转化为向量之间的计算，免除了符号的搜索匹配过程，因而推理计算更加高效。但向量表示的最大问题是丢失了可解释性，因为向量计算实际上丢失了符号推理的过程。只能得到一个分数（Score）评估结果的真或假，但并不知道为什么能得出这样的结果。此外，基于表示学习的方法还依赖于图谱中有足够多的训练样本。但知识图谱很多时候是高度稀疏的，即：很多实体只有少量甚至没有关系连接。对于那些训练样本不充分的实体，很难学习到好的向量表示，当然也会影响到推理的结果。

基于图神经网络的知识图谱推理

既然知识图谱通常有丰富的图结构，图神经网络方法当然也可以用来处理知识图谱数据。图神经网络善于捕获图的结构特征，例如，如果希望学习Rome城市的向量表示，那么它在图谱中的邻居节点，甚至多跳范围之外的远距离节点都有可能对它的表示产生影响。传统的图神经网络更多的是处理无标记的纯图模型，对于知识图谱需要做不同的处理。例如R-GCN首先对某个节点的边按关系类型进行区分，然后再用传统的GCN模型对节点特征进行聚合。后面会更具体地介绍这类模型的实现细节。图神经网络可以为图谱推理获得更多的图结构方面的特征，如下图所示。但图谱稀疏性问题则更为突出，因此图神经网络推理模型不适合图结构比较稀疏的场景，例如常识类知识图谱的表示学习。此外，图神经网络不仅可以用来对知识图谱进行推理，也可以做更加深度的挖掘和分析。

符号推理与表示学习的融合

符号知识的向量化表示更易于捕获隐含的不确定性知识，向量空间的连续性也使得基于向量的推理计算更易于泛化，并免于严格的符号逻辑匹配。然而，通过可微过程学习出的数值化知识表示虽然对机器友好，但人不可理解；同时，向量化的推理计算丢失了对推理链的跟踪，导致推理结果不可解释。将符号规则与表示学习相结合可以在一定程度上解决这一问题。一方面，在向量表示的学习过程中，植入符号规则的学习过程可以利用同步学习出的规则增强推理结果的可解释性。另外一方面，将人工构建和机器学习出的符号规则与向量表示的学习相耦合，也可以进一步在表示学习过程中植入逻辑层的先验知识，从而使得向量表示更易于实现符号逻辑推理。因此，符号逻辑与表示学习相互补充是解决表示学习可解释性的一种重要途径。更进一步，符号逻辑的向量化和神经网络化也使得感知层的任务（抽取、识别）能和认知层的任务（理解、推理）能够在统一的表示空间完成，因此，也是感知和认知进一步融合的未来主要发展趋势之一，如下图所示：

参考文献：
[1] 陈华钧.知识图谱导论[M].电子工业出版社, 2021
[2] 邵浩, 张凯, 李方圆, 张云柯, 戴锡强. 从零构建知识图谱[M].机械工业出版社, 2021