欧几里得空间

  线性空间里最重要的就是欧几里得空间了，这是线性代数学习绕不过去的槛。欧几里得空间，学习起来我觉得吧，主要是三个点：内积、长度、夹角。首先欧几里得空间，是是空间，所以它的符号是 $R^n$,比如三维空间符号就是 $R^3$，对应的复空间的符号是 $C^n$,但是本文不讲复空间。

1 欧几里得范数

  欧几里得空间里每个向量的模长，也就是向量的长度，有个高大上的名词，叫欧几里得范数,英文euclidean norm。这个范数是怎么定义的呢？
$$||x||=\sqrt{\sum _{i=1}^n{x}_i^2}$$
  比如向量$(1,1,1{)}^T$的欧几里得范数就是$\sqrt{1^2+1^2+1^2}=\sqrt{3}$.欧几里得范数实际上是向量到$0$点的距离.这个距离就是它的长度，也叫模长。当然这个比较好理解，就算不学线性代数，我们利用中学数学的勾股定理，也可以推出这个公式。

2 距离

  在中学数学里，我们知道两点之间的距离是$\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$,欧几里得空间，无论多少维度，都是在这个基础之上的。把这个公式拓展到n维，欧几里得空间的距离公式就是：
$$|x-y|=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$
  比如向量$(1,1,1{)}^T$到向量$(2,2,3{)}^T$的距离就是$\sqrt{(1-2{)}^2+(1-2{)}^2+(1-3{)}^2}=\sqrt{6}$.

3 标准内积

  标准内积是用来计算向量夹角的。这个夹角公式如下：
$$x\cdot y=|x||y|\cos \theta$$
  而公式中的$x\cdot y$就是标准内积standard inner product，也叫点积dot product。公式如下：
$$x\cdot y=\sum _{i=1}^n{x}_i{y}_i$$
  有了标准内积，就很容易计算两个向量之间的夹角了。在实际应用中，也用欧几里得空间的向量夹角来求两个事物之间的相关性。
  在矩阵理论里，对标准内积进行了扩展，所以欧几里得空间的内积也被称为标准内积，以同广义的内积区分开来。因为本文只讲欧几里得空间，所以就不过多讲内积了。

4 柯西-施瓦茨不等式

  这个不等式的内容就是：
$$|x\cdot y|\le |x||y|$$
  这个通过夹角的定义，就可以很容易的证明出来。

5 正交

  正交orthogonal，也就是垂直perpendicular，前者是代数的概念，后者是几何里的概念，意思是一样的。垂直的话，夹角就是$\frac{\pi }{2}$,而$\cos \frac{\pi }{2}=0$,所以标准内积就是0，那么正交就很容易判断了。
$$x\cdot y=\sum _{i=1}^n{x}_i{y}_i=0$$

6 叉乘

  叉乘只在三维欧几里得空间有定义，等于是一维、二维、四维或其他维度是没有外积的。三维比较特殊哈，外积的定义如下：
x × y = ( x 2 y 3 − x 3 y 2 x 3 y 1 − x 1 y 3 x 1 y 2 − x 2 y 1 ) x\times y=\begin{pmatrix}x_2y_3-x_3y_2\\x_3y_1-x_1y_3\\x_1y_2-x_2y_1\end{pmatrix} x×y= ​x2​y3​−x3​y2​x3​y1​−x1​y3​x1​y2​−x2​y1​​ ​
  两个向量围成的平行四边形parallelogram的面积，就是两个向量叉乘后的模长，公式如下：
$$a=|x\times y|$$
  我举个例子,虽然是个二维的例子，但是二维可以表示为第三维为0.

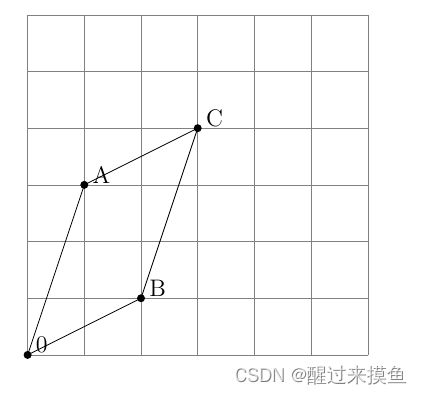
  很容易看出，这个平行四边形的面积是5，那我们验证下：
x = ( 1 3 0 ) , y = ( 2 1 0 ) x × y = ( 3 × 0 − 0 × 1 0 × 2 − 1 × 0 1 × 1 − 3 × 2 ) = ( 0 0 − 5 ) ∣ x × y ∣ = 5 x=\begin{pmatrix}1\\3\\0\end{pmatrix}, y=\begin{pmatrix}2\\1\\0\end{pmatrix}\\ x\times y = \begin{pmatrix}3\times 0-0\times 1\\0\times 2-1\times 0\\1\times 1-3\times 2\end{pmatrix}= \begin{pmatrix}0\\0\\-5\end{pmatrix}\\ |x\times y|=5 x= ​130​ ​,y= ​210​ ​x×y= ​3×0−0×10×2−1×01×1−3×2​ ​= ​00−5​ ​∣x×y∣=5
  验证无误啊。当然二维的面积其实用两个向量拼成一个矩阵，求它的行列式的绝对值就可以了。

7 平行四边形法则

  欧几里得空间里的向量加法，满足平行四边形法则，这个我们小时候在做物理题，力的合成，就是平行四边形法则。举个例子：

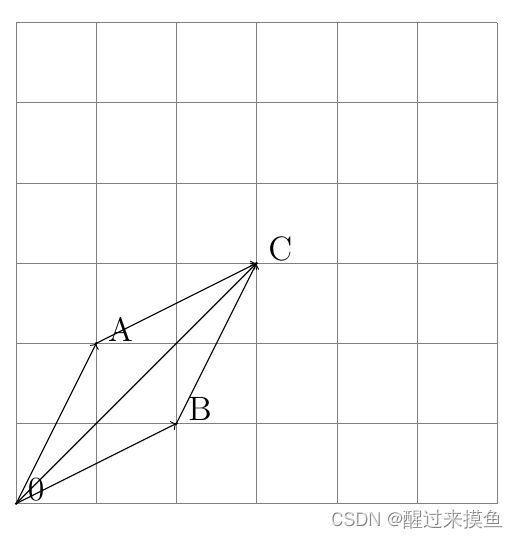
  上图就是向量的加法：
$$\begin{gathered} x=\left(\begin{array}{c}1\\ 2\end{array}\right),y=\left(\begin{array}{c}2\\ 1\end{array}\right) \\ x+y=\left(\begin{array}{c}3\\ 3\end{array}\right) \end{gathered}$$

8 欧几里得运动

  欧几里得运动Euclidean motion，实际上是一个映射，等价为先线性变换再做加法。也就是说有一个欧几里得运动T，它作用于一个向量的效果是$T(x)$等价于$Ax+b$。这就是著名的欧几里得运动公式：
$$T(x)=Ax+b$$
  仅仅这样还不算一个欧几里得运动，欧几里得运动必须保证变换后距离不变，也就是：
$$|T(x)-T(y)|=|x-y|$$
  什么意思呢？也就是先做旋转拉伸变换再平移。我们知道平移是不会改变两个点变换后的距离的，所以公式中的$Ax+b$的$b$不需要考虑。唯一考虑的就是$A$,事实上，数学家们早就证明了，一个变换是欧几里得运动的充分必要条件是$A$为正交矩阵。需要注意的是欧几里得运动不是线性变换，不是所有映射都是线性变换的。举个例子，下面的变换就是欧几里得运动：
$$T(x)=x+b$$
  正交阵的条件是$A^{T}A=A{A}^T=E$,$E$是单位矩阵。其实欧几里得运动就是说线性变换A如果是正交矩阵则不会改变向量之间的距离。