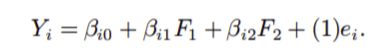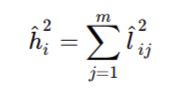python因子分析案例_Python因子分析简介

因子分析(FA)是一种探索性数据分析方法, 用于从一组观察到的变量中搜索有影响力的潜在因子或潜在变量。通过减少变量的数量, 它有助于数据解释。它从所有变量中提取最大共同方差, 并将它们放入一个共同得分。

因子分析广泛应用于市场研究, 广告, 心理学, 金融和运营研究。市场研究人员使用因素分析来识别价格敏感的客户, 识别影响消费者选择的品牌特征, 并帮助理解分销渠道的渠道选择标准。

在本教程中, 你将涵盖以下主题：

因子分析

因子分析的类型

确定因素数

因子分析与主成分分析

python中的因素分析

充足性测试

解释结果

因素分析的利弊

总结

因子分析

因子分析是线性统计模型。它用于解释观察变量之间的方差, 并将一组观察变量浓缩为称为因子的未观察变量。观测变量建模为因子和误差项的线性组合(来源)。因子或潜在变量与具有共同响应模式的多个观察变量相关。每个因素都说明了观察变量中的特定方差量。通过减少变量的数量, 它有助于数据解释。

因子分析是一种研究感兴趣的变量X1, X2, ……, X1是否与较少数量的不可观察因子F1, F2, ……, Fk线性相关的方法。

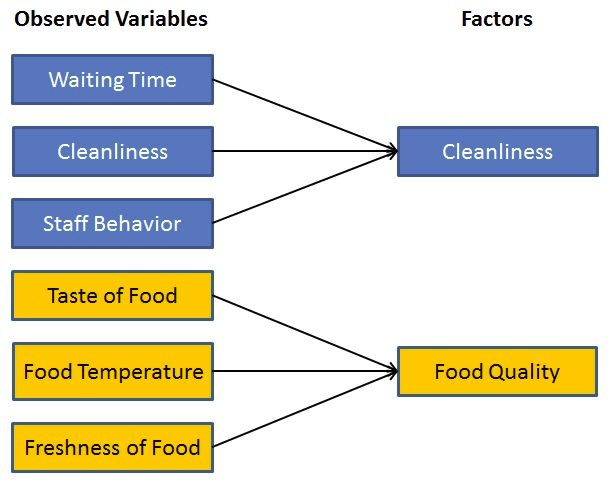
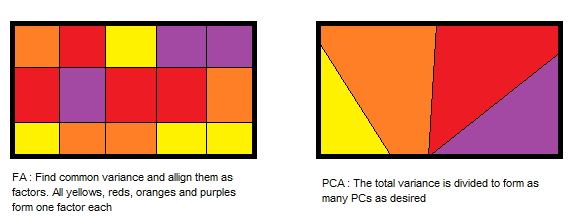
来源：此图像是根据我在因子分析说明中找到的图像重新创建的。该图提供了因素分析的完整视图。

假设：

数据中没有异常值。

样本数量应大于因子。

不应有完美的多重共线性。

变量之间不应存在同质性。

因子分析的类型

探索性因素分析：这是社会和管理研究人员中最流行的因素分析方法。它的基本假设是, 任何观察到的变量都与任何因素直接相关。

验证性因素分析(CFA)：其基本假设是每个因素都与一组特定的观察变量相关联。 CFA确认基本要求。

因子分析如何工作？

因子分析的主要目的是减少观察变量的数量并发现不可观察的变量。这些未观察到的变量有助于市场研究人员完成调查。观察变量到未观察变量的这种转换可以通过两个步骤来实现：

因子提取：在此步骤中, 使用方差划分方法(例如主成分分析和公共因子分析)选择因子的数量和提取方法。

因子轮换：在这一步骤中, 轮换尝试将因子转换为不相关的因子, 这是提高总体可解释性的主要目标。有很多可用的旋转方法, 例如：Varimax旋转方法, Quartimax旋转方法和Promax旋转方法。

术语

是什么因素？

一个因素是一个潜在变量, 它描述了观察到的变量数量之间的关联。因素的最大数量等于观察到的变量的数量。每个因素都说明观测变量存在一定差异。方差量最低的因素被删除。因子也称为潜在变量或隐藏变量或未观察到的变量或假设变量。

负载因素是什么？

因子加载是一个矩阵, 该矩阵显示每个变量与基础因子的关系。它显示了观测变量和因子的相关系数。它显示了观察到的变量解释的方差。

什么是特征值？

特征值代表方差, 由总方差解释每个因素。它也被称为特征根。

什么是社区？

共同点是每个变量的平方加载总和。它代表共同方差。它的范围是0-1, 接近1的值表示更多的方差。

什么是因子旋转？

轮换是一种更好地解释因子分析的工具。旋转可以是正交的或倾斜的。它以清晰的负载模式重新分配了共性。

选择因素数

凯撒(Kaiser)准则是一种分析方法, 该方法基于将选择因数解释的方差的较大比例。特征值是确定因子数量的良好标准。通常, 将大于1的特征值视为特征的选择标准。

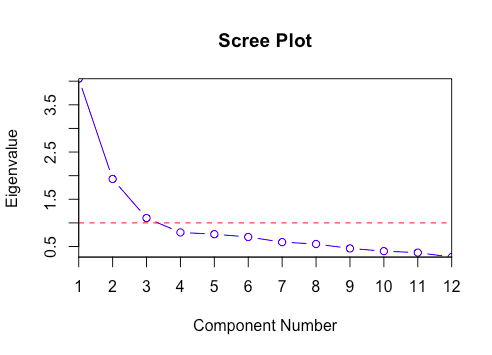
图形化方法基于因子特征值的可视表示, 也称为卵石图。此卵石图有助于我们确定曲线成为弯头的因素的数量。

资源

因子分析与主成分分析

PCA组件说明最大方差, 而因子分析说明数据中的协方差。

PCA组件彼此完全正交, 而因子分析不需要因子正交。

PCA分量是观察变量的线性组合, 而在FA中, 观察变量是未观察变量或因子的线性组合。

PCA组件无法解释。在FA中, 潜在因素是可标记和可解释的。

PCA是一种降维方法, 而因子分析是潜在变量方法。

PCA是一种因素分析。 PCA是观察性的, 而FA是一种建模技术。

资源

使用factor_analyzer软件包在python中进行因素分析

导入所需的库

# Import required libraries

import pandas as pd

from sklearn.datasets import load_iris

from factor_analyzer import FactorAnalyzer

import matplotlib.pyplot as plt

加载数据中

让我们对BFI(基于人格评估项目的数据集)进行因素分析, 这些因素是使用6点回应量表收集的：1个非常不准确, 2个中度不准确, 3个略有不正确4个略有准确, 5个中度和6个非常准确。你也可以从以下链接下载此数据集：https://vincentarelbundock.github.io/Rdatasets/datasets.html

df= pd.read_csv("bfi.csv")

预处理数据

df.columns

Index(['A1', 'A2', 'A3', 'A4', 'A5', 'C1', 'C2', 'C3', 'C4', 'C5', 'E1', 'E2', 'E3', 'E4', 'E5', 'N1', 'N2', 'N3', 'N4', 'N5', 'O1', 'O2', 'O3', 'O4', 'O5', 'gender', 'education', 'age'], dtype='object')

# Dropping unnecessary columns

df.drop(['gender', 'education', 'age'], axis=1, inplace=True)

# Dropping missing values rows

df.dropna(inplace=True)

df.info()

Int64Index: 2436 entries, 0 to 2799

Data columns (total 25 columns):

A1 2436 non-null float64

A2 2436 non-null float64

A3 2436 non-null float64

A4 2436 non-null float64

A5 2436 non-null float64

C1 2436 non-null float64

C2 2436 non-null float64

C3 2436 non-null float64

C4 2436 non-null float64

C5 2436 non-null float64

E1 2436 non-null float64

E2 2436 non-null float64

E3 2436 non-null float64

E4 2436 non-null float64

E5 2436 non-null float64

N1 2436 non-null float64

N2 2436 non-null float64

N3 2436 non-null float64

N4 2436 non-null float64

N5 2436 non-null float64

O1 2436 non-null float64

O2 2436 non-null int64

O3 2436 non-null float64

O4 2436 non-null float64

O5 2436 non-null float64

dtypes: float64(24), int64(1)

memory usage: 494.8 KB

df.head()

A1

A2

A3

A4

A5

C1

C2

C3

C4

C5

…

N1

N2

N3

N4

N5

O1

O2

O3

O4

O5

0

2.0

4.0

3.0

4.0

4.0

2.0

3.0

3.0

4.0

4.0

…

3.0

4.0

2.0

2.0

3.0

3.0

6

3.0

4.0

3.0

1

2.0

4.0

5.0

2.0

5.0

5.0

4.0

4.0

3.0

4.0

…

3.0

3.0

3.0

5.0

5.0

4.0

2

4.0

3.0

3.0

2

5.0

4.0

5.0

4.0

4.0

4.0

5.0

4.0

2.0

5.0

…

4.0

5.0

4.0

2.0

3.0

4.0

2

5.0

5.0

2.0

3

4.0

4.0

6.0

5.0

5.0

4.0

4.0

3.0

5.0

5.0

…

2.0

5.0

2.0

4.0

1.0

3.0

3

4.0

3.0

5.0

4

2.0

3.0

3.0

4.0

5.0

4.0

4.0

5.0

3.0

2.0

…

2.0

3.0

4.0

4.0

3.0

3.0

3

4.0

3.0

3.0

5行×25列

充足性测试

在执行因子分析之前, 你需要评估我们数据集的”可分解性”。可分解性意味着”我们可以在数据集中找到这些因素吗？”。有两种方法可以检查可分解性或抽样是否足够：

巴特利特的测验

Kaiser-Meyer-Olkin检验

巴特利特(Bartlett)的球形度检验使用观察到的相关矩阵和恒等矩阵检查观察到的变量是否相互关联。如果测试发现统计上不重要, 则不应使用因子分析。

from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity

chi_square_value, p_value=calculate_bartlett_sphericity(df)

chi_square_value, p_value

(18146.065577234807, 0.0)

在此Bartlett检验中, p值为0。该检验具有统计学意义, 表明所观察到的相关矩阵不是恒等矩阵。

Kaiser-Meyer-Olkin(KMO)测试可测量数据是否适合进行因子分析。它确定每个观察变量和完整模型的充分性。 KMO估计所有观察变量之间的方差比例。较低的比例ID更适合因子分析。 KMO值介于0到1之间。KMO值小于0.6被认为是不合适的。

from factor_analyzer.factor_analyzer import calculate_kmo

kmo_all, kmo_model=calculate_kmo(df)

kmo_model

0.8486452309468382

我们的数据的总体KMO为0.84, 非常好。该值表示你可以继续进行计划的因素分析。

选择因素数

要选择因子数量, 可以使用Kaiser准则和卵石图。两者均基于特征值。

# Create factor analysis object and perform factor analysis

fa = FactorAnalyzer()

fa.analyze(df, 25, rotation=None)

# Check Eigenvalues

ev, v = fa.get_eigenvalues()

ev

原始特征值

0

5.134311

1

2.751887

2

2.142702

3

1.852328

4

1.548163

5

1.073582

6

0.839539

7

0.799206

8

0.718989

9

0.688089

10

0.676373

11

0.651800

12

0.623253

13

0.596563

14

0.563091

15

0.543305

16

0.514518

17

0.494503

18

0.482640

19

0.448921

20

0.423366

21

0.400671

22

0.387804

23

0.381857

24

0.262539

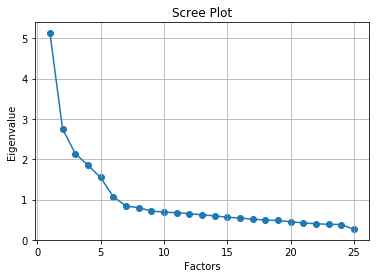
在这里, 你只能看到6因子特征值大于1。这意味着我们只需要选择6个因素(或未观察到的变量)。

# Create scree plot using matplotlib

plt.scatter(range(1, df.shape[1]+1), ev)

plt.plot(range(1, df.shape[1]+1), ev)

plt.title('Scree Plot')

plt.xlabel('Factors')

plt.ylabel('Eigenvalue')

plt.grid()

plt.show()

卵石图方法为每个因子及其特征值绘制一条直线。特征值大于1的数量被认为是因子的数量。

在这里, 你只能看到6因子特征值大于1。这意味着我们只需要选择6个因素(或未观察到的变量)。

执行因素分析

# Create factor analysis object and perform factor analysis

fa = FactorAnalyzer()

fa.analyze(df, 6, rotation="varimax")

fa.loadings

因子1

因素2

因素3

因素4

因素5

因子6

A1

0.040783

0.095220

0.048734

-0.113057

-0.530987

0.161216

A2

0.235538

0.033131

0.133714

0.063734

0.661141

-0.006244

A3

0.343008

-0.009621

0.121353

0.033990

0.605933

0.160106

A4

0.219717

-0.081518

0.235140

-0.125338

0.404594

0.086356

A5

0.414458

-0.149616

0.106382

0.030977

0.469698

0.236519

C1

0.077248

-0.004358

0.554582

0.190124

0.007511

0.095035

C2

0.038370

0.068330

0.674545

0.087593

0.057055

0.152775

C3

0.031867

-0.039994

0.551164

-0.011338

0.101282

0.008996

C4

-0.066241

0.216283

-0.638475

-0.143846

-0.102617

0.318359

C5

-0.180812

0.284187

-0.544838

0.025837

-0.059955

0.132423

E1

-0.590451

0.022280

0.053915

-0.071205

-0.130851

0.156583

E2

-0.684578

0.233624

-0.088497

-0.045561

-0.116716

0.115065

E3

0.556774

-0.000895

0.103390

0.241180

0.179396

0.267291

E4

0.658395

-0.136788

0.113798

-0.107808

0.241143

0.158513

E5

0.507535

0.034490

0.309813

0.200821

0.078804

0.008747

N1

0.068011

0.805806

-0.051264

-0.074977

-0.174849

-0.096266

N2

0.022958

0.789832

-0.037477

0.006726

-0.141134

-0.139823

N3

-0.065687

0.725081

-0.059039

-0.010664

-0.019184

0.062495

N4

-0.345072

0.578319

-0.162174

0.062916

0.000403

0.147551

N5

-0.161675

0.523097

-0.025305

-0.161892

0.090125

0.120049

O1

0.225339

-0.020004

0.133201

0.479477

0.005178

0.218690

O2

-0.001982

0.156230

-0.086047

-0.496640

0.043989

0.134693

O3

0.325954

0.011851

0.093880

0.566128

0.076642

0.210777

O4

-0.177746

0.207281

-0.005671

0.349227

0.133656

0.178068

O5

-0.014221

0.063234

-0.047059

-0.576743

-0.057561

0.135936

因子1对E1, E2, E3, E4和E5(外推)具有较高的因子负载

因子2对N1, N2, N3, N4和N5具有较高的因子负荷(神经病)

因子3对C1, C2, C3, C4和C5具有很高的因子负荷(尽责程度)

因子4对O1, O2, O3, O4和O5(Opennness)具有高因子负载

因子5对A1, A2, A3, A4和A5具有较高的因子负载(令人满意)

因子6没有任何变量的高价, 也不容易解释。如果仅考虑五个因素, 那将是一件好事。

让我们对5个因素进行因素分析。

# Create factor analysis object and perform factor analysis using 5 factors

fa = FactorAnalyzer()

fa.analyze(df, 5, rotation="varimax")

fa.loadings

因子1

因素2

因素3

因素4

因素5

A1

0.040465

0.111126

0.022798

-0.077931

-0.428166

A2

0.213716

0.029588

0.139037

0.062139

0.626946

A3

0.317848

0.009357

0.109331

0.056196

0.650743

A4

0.204566

-0.066476

0.230584

-0.112700

0.435624

A5

0.393034

-0.122113

0.087869

0.066708

0.537087

C1

0.070184

0.010416

0.545824

0.209584

0.038878

C2

0.033270

0.089574

0.648731

0.115434

0.102782

C3

0.023907

-0.030855

0.557036

-0.005183

0.111578

C4

-0.064984

0.240410

-0.633806

-0.107535

-0.037498

C5

-0.176395

0.290318

-0.562467

0.036822

-0.047525

E1

-0.574835

0.042819

0.033144

-0.058795

-0.104813

E2

-0.678731

0.244743

-0.102483

-0.042010

-0.112517

E3

0.536816

0.024180

0.083010

0.280877

0.257906

E4

0.646833

-0.115614

0.102023

-0.073422

0.306101

E5

0.504069

0.036145

0.312899

0.213739

0.090354

N1

0.078923

0.786807

-0.045997

-0.084704

-0.216363

N2

0.027301

0.754109

-0.030568

-0.010304

-0.193744

N3

-0.061430

0.731721

-0.067084

-0.004217

-0.027712

N4

-0.345388

0.590602

-0.178902

0.075225

0.005886

N5

-0.161291

0.537858

-0.037309

-0.149769

0.100931

O1

0.213005

-0.002224

0.115080

0.504907

0.061550

O2

0.004560

0.175788

-0.099729

-0.468925

0.081809

O3

0.310956

0.026736

0.076873

0.596007

0.126889

O4

-0.191196

0.220582

-0.021906

0.369012

0.155475

O5

-0.005347

0.085401

-0.062730

-0.533778

-0.010384

# Get variance of each factors

fa.get_factor_variance()

因子1

因素2

因素3

因素4

因素5

SS负荷

2.473090

2.709633

2.041106

1.522153

1.844498

比例变量

0.098924

0.108385

0.081644

0.060886

0.073780

Cumulative Var

0.098924

0.207309

0.288953

0.349839

0.423619

5个因素解释了总计42％的累积方差。

因素分析的利弊

因子分析探索大型数据集并找到相互关联的关联。它可以将观察到的变量减少为几个未观察到的变量, 或者识别相互关联的变量组, 这有助于市场研究人员压缩市场状况, 并找到消费者品味, 偏好和文化影响力之间的隐藏关系。而且, 它有助于改进问卷以供将来进行调查。因素使数据解释更加自然。

因子分析的结果是有争议的。它的解释可能是有争议的, 因为可以对相同的数据因素进行多种解释。之后, 因素识别和因素命名需要领域知识。

总结

恭喜, 你已完成本教程的结尾！

在本教程中, 你学习了什么是因子分析。不同类型的因素分析, 因素分析如何工作, 基本因素分析术语, 选择因素数量, 主成分分析和因素分析的比较, 使用python FactorAnalyzer软件包在python中的实现以及因素分析的利弊。

我期待听到任何反馈或问题。你可以通过发表评论来提出问题, 我会尽力回答。

如果你想了解有关Python中因素的更多信息, 请参加srcmini的Python无监督学习课程。