论文阅读 (64)：Weakly-supervised Video Anomaly Detection with Robust Temporal Feature Magnitude Learning

1 引入

1.1 题目

  2021CVPR：用于弱监督视频异常检测的健壮性时间特征量级学习 (Weakly-supervised video anomaly detection with robust temporal feature magnitude learning)

1.2 代码

  Torch：https://github.com/tianyu0207/RTFM

1.3 摘要

  弱监督视频级别异常检测是一个典型的多示例学习 (Multi-instance learning, MIL) 问题，每一个视频看作是一个包含多个帧的包，目的是判断包中是否包含异常片段。目前的检测方法性能优异，但它们对正实例，即异常视频中罕见的异常片段的识别，在很大程度上受到了支配性负实例的影响，特别是当异常事件是与正常事件相比时只有很小差异的细微异常时。在许多忽略重要视频时间依赖性的方法中，这个问题更加严重。
  为了解决这个问题，提出了健壮性时间特征量级学习：
  1）训练了一个特征量级学习函数来有效地识别正实例，大大提高了MIL方法对异常视频负实例的鲁棒性；
  2）采用空洞卷积 (Dilated convolutions) 和自注意力机制来捕获长距离和短距离的时间依赖性，从而更可靠地学习特征量级。

1.4 Bib

@inproceedings{Tian:2021:49754986,
author		=	{Yu Tian and Guan Song Pang and Yuan Hong Chen and Rajvinder Singh and Johan W Verjans and Gustavo Carneiro},
title		=	{Weakly-supervised video anomaly detection with robust temporal feature magnitude learning},
booktitle	=	{{IEEE/CVF} International Conference on Computer Vision},
pages		=	{4975--4986},
year		=	{2021},
url			=	{https://openaccess.thecvf.com/content/ICCV2021/html/Tian_Weakly-Supervised_Video_Anomaly_Detection_With_Robust_Temporal_Feature_Magnitude_Learning_ICCV_2021_paper.html}
}

2 RTFM

  RTFM的目的是基于弱标记视频来最大程度地区分异常视频和正常视频。给定训练视频的集合$\mathcal{D}=\{({\mathbf{F}}_i,y_i){\}}_{i=1}^{|\mathcal{D}|}$，其中$\mathbf{F}\in \mathcal{F}\subset {\mathbb{R}}^{T\times D}$是$T$个视频帧的$D$维预计算特征，例如I3D和C3D；$y\in \mathcal{Y}=\{0,1\}，1$表示异常，$0$反之。令$r_{\theta ,\varphi }(\mathbf{F})=f_{\varphi }(s_{\theta }(\mathbf{F}))$表示RTFM模型，其将返回一个$T$维特征$[0,1{]}^T$以表示视频帧是否异常。
  模型的训练包括包括端到端多尺度时间特征学习、特征量级学习，以及MIL 分类器。损失函数如下：
$$\underset{\theta ,\varphi }{\min }\sum _{i,j=1}^{|\mathcal{D}|}{\ell }_s(s_{\theta }({\mathbf{F}}_i),s_{\theta }({\mathbf{F}}_j),y_i,y_j)+{\ell }_f(f_{\varphi }(s_{\theta }({\mathbf{F}}_i)),y_i),$$其中$s_{\theta }:\mathcal{F}\to \mathcal{X}\subset {\mathbb{R}}^{T\times D}$是时间特征提取器、$f_{\varphi }:\mathcal{X}\to [0,1{]}^T$是一个帧级分类器、${\ell }_s(\cdot )$表示最大化正常与异常视频top-$k$个帧特征之间的差异性的损失函数，以及$f_{\varphi }(\cdot )$是一个使用以上top-$k$个特征的训练损失。

2.1 理论动机

  Top-$k$中的基本假设为，正包中包含最少数量的正实例，负包也包含正实例只是数量更少，它进一步假设分类器可以分离正实例和负实例。我们的问题与其不同，因此负包中并不包含正实例，当然也没有其分类器假设。
  遵循先前的命名规则，令$\mathbf{X}=s_{\theta }(\mathbf{F})$表示提取的视频时间特征，其中每一个帧特征${\mathbf{x}}_t$对应$\mathbf{X}$的每一行。令${\mathbf{x}}^{+}\sim P_x^{+}(\mathbf{x})$和${\mathbf{x}}^{-}\sim P_x^{-}(\mathbf{x})$分别表示异常帧和正常帧。一个异常视频${\mathbf{X}}^{+}$包含$\mu$个来自$P_x^{+}(\mathbf{x})$的帧，余下$(T-\mu )$来自$P_x^{-}(\mathbf{x})$，正常视频中的所有帧则均来自$P_x^{-}(\mathbf{x})$。
  为了学习一个能够区分视频和帧是否异常的函数，定义了一个使用帧的特征量级进行分类的函数，对此定义一个更加温和的假设如下：
$$\mathbb{E}[\Vert {\mathbf{x}}^{+}{\Vert }_2]\ge \mathbb{E}[\Vert {\mathbf{x}}^{-}{\Vert }_2].$$这意味着通过学习来自$\mathbf{X}$的帧级别特征，正常帧的应当有相较于异常帧更小的特征量级。基于以上假设和视频中的top-$k$特征的平均特征量级的优化定义如下：
$$g_{\theta ,k}(\mathbf{X})=\underset{{\Omega }_k(\mathbf{X})\subseteq \{{\mathbf{x}}_t{\}}_{t=1}^T}{\max }\frac{1}{k}\sum _{{\mathbf{x}}_t\in {\Omega }_k(\mathbf{X})}\Vert {\mathbf{x}}_t{\Vert }_2,\text{\hspace{1em}(2)}$$其中$g_{\theta ,k}(\cdot )$是由$\theta$参数化的函数、${\Omega }_k(\mathbf{X})$是$\{{\mathbf{x}}_t\}$的大小为$k$的子集。异常视频与正常视频的可分离性 (separability) 定义为：
$$d_{\theta ,k}({\mathbf{X}}^{+},{\mathbf{X}}^{-})=g_{\theta ,k}({\mathbf{X}}^{+})-g_{\theta ,k}({\mathbf{X}}^{-}).\text{\hspace{1em}(3)}$$  定义来自${\Omega }_k({\mathbf{X}}^{+})$帧的异常概率为：
$$p_k^{+}({\mathbf{X}}^{+})=\frac{\min (\mu ,k)}{k+ϵ},$$其中$ϵ>0$，而对于所有来自${\Omega }_k({\mathbf{X}}^{-})$的帧，有$p_k^{+}({\mathbf{X}}^{-})=0$。这意味着在$k\le \mu$时，将于${\Omega }_k({\mathbf{X}}^{+})$的top-$k$个帧中找到异常帧。

  定理3.1：异常与正常视频的预期可分离性 假设$\mathbb{E}[\Vert {\mathbf{x}}^{+}{\Vert }_2]\ge \mathbb{E}[\Vert {\mathbf{x}}^{-}{\Vert }_2]$，其中${\mathbf{X}}^{+}$包含$\mu \in [1,T]$个异常实例和$(T-\mu )$个正常实例，以及${\mathbf{X}}^{-}$包含$T$个正常实例。令$D_{\theta ,k}(\cdot )$表示$d_{\theta ,k}(\cdot )$的随机变量：
  1）如果$0<k<\mu$，则
$$0\le \mathbb{E}[D_{\theta ,k}({\mathbf{X}}^{+},{\mathbf{X}}^{-})]\le \mathbb{E}[D_{\theta ,k+1}({\mathbf{X}}^{+},{\mathbf{X}}^{-})]$$  2）对于一个有限的$\mu$，有
$$\underset{k\to \infty }{\lim }\mathbb{E}[D_{\theta ,k}({\mathbf{X}}^{+},{\mathbf{X}}^{-})]=0.$$  该定理的第一部分意味着在$k\le \mu$时，随着$k$的增加，异常视频和正常视频之间的可分离性趋于增加，即使它包含一些正常样本。定理的第二部分意味着，当包含多个top实例时，由于正负包中的负实例数量过多，异常和正常视频的分数将变得无法区分。一个示意如图1，其中$\text{score}(\mathbf{X})=g_{\theta ,k}(\mathbf{X})$、$\Delta \text{score}({\mathbf{X}}^{+},{\mathbf{X}}^{-})=d_{\theta ,k}({\mathbf{X}}^{+},{\mathbf{X}}^{-})$，以及$ϵ=0.4$。该定理指明：
  1）当$k\le \mu$时，通过最大化正常视频与异常视频top-$k$个帧之间的可分离性，能够加速异常视频与帧的分类过程；
  2）使用top-$k$个特征可以更有效地训练帧分类器，因为异常视频中的top-$k$个实例大部分都是异常的，并且将使用top-$k$个正常片段。此外，仅使用top-$k$的另一个原因是所设计的方法可以在相当少的训练样本下进行。

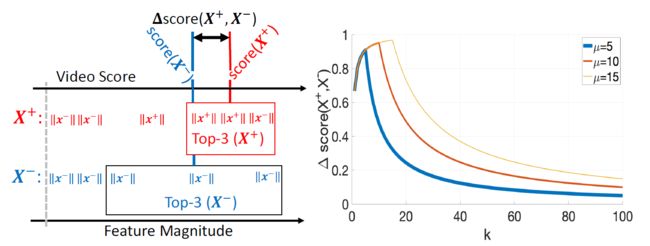
  图1：RTFM训练一个特征量级学习函数来高效地检测异常帧并提升MIL方法对异常视频中正常帧的健壮性。左图：异常视频与正常视频的时间特征量级。假设$\mu =3$表示异常视频中异常帧的数量，将最大化异常视频与正常视频的分数差异$\Delta \text{score}({\mathbf{X}}^{+},{\mathbf{X}}^{-})$。参与计算的帧为$k\le \mu$个具有最大时间特征量级帧。右图：$\Delta \text{score}({\mathbf{X}}^{+},{\mathbf{X}}^{-})$在$k\le \mu$时逐渐增大，而将$k>\mu$时逐渐降低。这表明$k\approx \mu$时RTFM在正负视频之间提供了一个很好的差异，即使一些正常帧也具有较大的特征量级

2.2 多尺度时间特征学习

  受视频理解注意力机制的启发，所提出的多尺度时间网络 (multi-scale temporal network, MTN) 可以捕捉视频帧之间的多来源局部时间依赖和全局时间依赖。MTN使用时域上的空洞卷积金字塔来学习视频帧的多尺度表示。空洞卷积通常应用于空间域，目的是在不损失分辨率的情况下扩展感受野。在这里，空洞卷积被用于时间维度，因为捕获相邻视频帧的多尺度时间依赖性以进行异常检测很重要。
  MTN从预计算特征$\mathbf{F}=[{\mathbf{f}}_d{]}_{d=1}^D$上学习多尺度时间特征。对于给定特征${\mathbf{f}}_d\in {\mathbb{R}}^T$，1D空洞卷积定义如下：
$${\mathbf{f}}_k^{(l)}=\sum _{d=1}^D{\mathbf{W}}_{k,d}^{(l)}{\ast }^{(l)}{\mathbf{f}}_d,\text{\hspace{1em}(4)}$$其中${\mathbf{W}}_{k,d}^{(l)}\in {\mathbb{R}}^W$表示卷积核、$k\in \{1,\dots ,D/4\}$、$l\in \{{\text{PDC}}_1,{\text{PDC}}_2,{\text{PDC}}_3\}$、$W$表示卷积核大小、${\ast }^{(l)}$基于索引$l$的卷积操作，以及${\mathbf{f}}_k^{(l)}$表示应用于时间维度的空间卷积的输出特征。空洞因子$\{{\text{PDC}}_1,{\text{PDC}}_2,{\text{PDC}}_3\}$设置为$\{1,2,4\}$。
  自注意力机制用于补充视频帧之间的全局时间依赖，其已在视频理解中的长期时间依赖、图像分类，以及对象检测展现出优异性能。受到GCN中对全局时间信息的建模，空间自注意力被重写以适应时间维度并捕捉全局时间上下文，即生成一个用于评估帧之间关系的注意力图$\mathbf{M}\in {\mathbb{R}}^{T\times T}$。
  时间注意力模型 (Temporal self-attention, TSA) ：
  1）首先使用$1\times 1$卷积减小空间维度，即$\mathbf{F}\in {\mathbf{R}}^{T\times D}\to {\mathbf{F}}^{(c)}=Con{v}_{1\times 1}(\mathbf{F})\in {\mathbb{R}}^{T\times D/4}$；
  2）应用3个独立的$1\times 1$卷积层，将${\mathbf{F}}^{(c)}$转换为${\mathbf{F}}^{(ci)}=Con{v}_{1\times 1}({\mathbf{F}}^{(\mathbf{c})})$，其中$i\in \{1,2,3\}$；
  3）构建注意力图：
$$\mathbf{M}=({\mathbf{F}}^{c1})(F^{(c2)}{)}^T,$$其用于获取
$${\mathbf{F}}^{(c4)}=Con{v}_{1\times 1}({\mathbf{MF}}^{c3})$$  4）计算：
$${\mathbf{F}}^{TSA}={\mathbf{F}}^{c4}+{\mathbf{F}}^{c3}.\text{\hspace{1em}(5)}$$  5）MTN的输出由PDC和MTN模块的输出串联构成：
$$\overline{\mathbf{F}}=[{\mathbf{F}}^{(l)}{]}_{l\in \mathcal{L}}\in \mathbf{T}\times \mathbf{D},$$其中$\mathcal{L}=\{{\text{PDC}}_1,{\text{PDC}}_2,{\text{PDC}}_3,\text{TSA}\}$；
  6）跳跃连接以获取包含原始特征与事件特征的表示：
$$\mathbf{X}=s_{\theta }(\mathbf{F})=\overline{\mathbf{F}}+\mathbf{F}.$$

2.3 特征量级学习

  首先提出一个关联$s_{\theta }(\mathbf{F})$的损失函数${\ell }_s$，其中来自正常视频的最大$k$个特征量级被最小化，而来自异常视频的该特征被最大化：
$${\ell }_s(s_{\theta }({\mathbf{F}}_i),s_{\theta }({\mathbf{F}}_j),y_i,y_j)=\{\begin{array}{ll}\max \left(0,m-d_{\theta ,k}({\mathbf{X}}_i,{\mathbf{X}}_j)\right)& ,y_i=1,y_j=0\\ 0& ,otherwise,\end{array}\text{\hspace{1em}(6)}$$其中$m$是预定义间隔、${\mathbf{X}}_i=s_{\theta }({\mathbf{F}}_i),{\mathbf{X}}_j$分别表示异常和正常视频，以及$d_{\theta ,k}(\cdot )$表示可分离性函数。

2.4 RTFM帧级分类器

  二元交叉熵损失函数基于${\Omega }_k(\mathbf{X})$来学习一个帧级分类器：
$${\ell }_f(f_{\varphi }(s_{\theta }(\mathbf{F}),y))=\sum _{\mathbf{x}\in {\Omega }_k(\mathbf{X})}-(y\log (f_{\varphi }(\mathbf{x}))+(1-y)\log (1-f_{\varphi }(\mathbf{x}))),$$其中$\mathbf{x}=s_{\theta }(\mathbf{f})$。注意${\ell }_f(\cdot )$通过时间平滑 (强制向量帧的异常得分相似)
$$(f_{\varphi }(s_{\theta }({\mathbf{f}}_{\mathbf{t}}))-f_{\varphi }(s_{\theta }({\mathbf{f}}_{\mathbf{t}-1})))$$和稀疏正则 (强加一个先验，表明异常事件在每个异常视频中都很少见)
$$\sum _{t=1}^T|f_{\varphi }(s_{\theta }({\mathbf{f}}_{\mathbf{t}}))|$$来实现。

3 实验

3.1 数据集和度量标准

  四个多场景基准数据集被使用：
  1）UCF-Crime是一个大规模异常检测数据集，包含来自真实街道和室内监控摄像头的1900个未修剪视频，总时长为128小时。与ShanghaiTech中的静态背景不同，UCF-Crime的背景更为复杂多样。训练集和测试集包含同样数量的异常和正常视频，其中训练集包含视频级标注，共1610，异常事件共13类；测试集包含帧级标注，共290。
  2）XD-Violence是一个近期提出的大规模多场景数据集，收集了现实生活电影、在线视频、体育视频流、监控摄像机，以及CCTV。数据集的总时长为217小时，包含4754 个未修剪视频，训练集具有视频级标签，测试集具有帧级标签。它是目前最大的公开视频异常检测数据集。
  3）ShanghaiTech是一个来自固定角度视频监控的中型数据集，包含307个正常视频和130个异常视频。原始数据集是异常检测任务的常用基准，其假设正常训练数据的可用性。Zhong等人通过选择异常测试视频的子集到训练数据中，以重组数据集并构建弱监督训练集，使训练集和测试集覆盖所有13个背景场景。
  4）UCSD-Peds是一个包含两个子数据集的小型数据集。Ped1和Ped2分别包含70和28个视频。通过随机选择6个异常视频和4个正常视频到训练集中，重新制定用于弱监督异常检测的数据集，其余的作为测试集。最终展示该过程10 次以上的平均结果。
  度量标准：帧级AUC作为所有数据集的衡量标准。XD-Violence额外使用平均精度 (Average precision, AP)。

3.2 实现细节

  1）每个视频被划分为32个帧；
  2）对于所有的数据集，设置公示6中的$m=100$，$k=3$；
  3）三个全连接层FC的节点分别设置为512、128，以及1，其后接ReLU函数，且设置丢弃率为0.7；
  4）预训练I3D和C3D的mix_5c和fc_6层分别提取2048维与4096维特征；
  5）空洞卷积的空洞率分别设置维1、2，以及4；
  6）每个空洞卷积分支使用$3\times 1$Conv1D；
  7）自注意力快使用$1\times 1$Conv1D；
  8）优化方法使用Adam，权重衰减设置为0.0005，批次大小64 (32异常32正常)，训练轮次50；
  9）ShanghaiTech和UCF-Crime学习率设置为0.001，XD-Violence设置为0.0001；
  10）使用Pytorch实现；
  11）对比方法的结果使用其与本方法网络骨架一致的发表结果。