贝尔曼最优方程(Bellman Optimality Equation)

本节使用 更新图的方式对 $V_{\pi }(s)$和 $q_{\pi }(s,a)$之间的关系进行详细说明，并在贝尔曼期望方程(Bellman Expectation Equation)基础上介绍 贝尔曼最优方程(Bellman Optimality Equation)。

目录

回顾 + 补充

上一节我们介绍了贝尔曼期望方程(Bellman Expectation Equation)，并重点介绍了状态价值函数$V_{\pi }(s)$和状态-动作价值函数$q_{\pi }(s,a)$之间的关系。
针对上一节中$G_t=R_{t+1}+\gamma G_{t+1}$成立需要满足的4个条件，本节使用更新图的方式对该步骤进行补充。

逻辑场景设置

对回溯图中出现的相关概念和条件进行设定：

• 状态集合$\mathcal{S}$属于离散型随机变量，共包含3种状态；
  $$\mathcal{S}=\{s_1,s_2,s_3\}$$
• 动作集合 $\mathcal{A}$属于离散型随机变量，共包含3种动作；
  $$\mathcal{A}=\{a_1,a_2,a_3\}$$
• 奖励集合$\mathcal{R}$属于离散型随机变量，共包含3种奖励；
  $$\mathcal{R}=\{r_1,r_2,r_3\}$$

从$S_t=s_1\to S_{t+1}$的状态转移过程如下图所示：

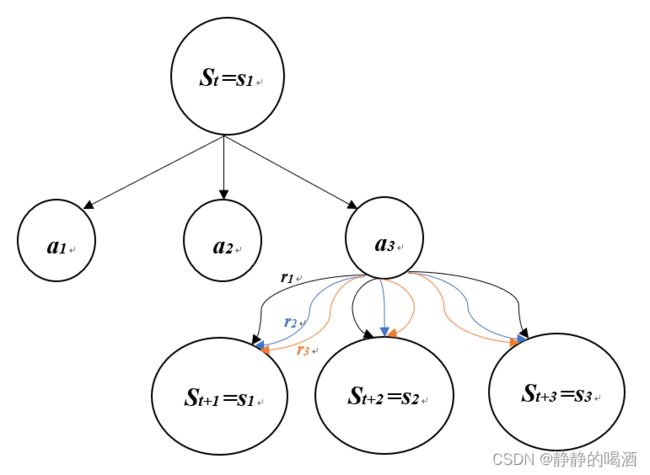
由上图可知，从$S_t=s_1$开始，存在3种动作选择方式：$a_1,a_2,a_3$；假设在$S_t=s_1,A_t=a_3$确定的情况下，系统内部状态由$S_t\to S_{t+1}$，由于奖励(Reward)同样也是离散的，转移过程中同样存在3种不同的选择方式：$r_1,r_2,r_3$。($a_1,a_2$下方同样存在和$a_3$相同的路径，为节省空间省略。)

上一节中“$G_t=R_{t+1}+\gamma G_{t+1}$成立需要满足的4个条件”对应的更新图如下图所示。橙黄色表示动作选择和状态转移过程。

贝尔曼最优方程

最优策略与最优价值函数

上一节我们介绍了2种价值函数：状态价值函数$V_{\pi }(s)$和状态-动作价值函数$q_{\pi }(s,a)$。利用强化学习方法解决任务意味着要寻找一个最优策略 ${\pi }^{\ast }\to$ 使智能体在使用该策略与环境交互过程中的回报始终比其他策略都要大。

最优状态价值函数

之前讲过，如何比较策略的优劣呢？自然是通过对应的价值函数进行比较，我们进行如下定义：

• 定义1：
  在当前时刻状态$S_t=s$的情况下，假设我们的策略$\pi (a\mid s)$是有穷的(策略的数量是可数的)，将所有策略全部计算状态价值函数$V_{\pi }(s)$,我们会产生一个关于$V_{\pi }(s)$的集合(其中${\pi }^{(1)},{\pi }^{(2)},{\pi }^{(3)}$,…表示不同策略)：
  $$\mathcal{V}=\{V_{{\pi }^{(1)}}(s),V_{{\pi }^{(2)}}(s),V_{{\pi }^{(3)}}(s)...\}$$
  我们从该集合中选择一个值最大的状态价值函数，记作$V_{\ast }(s)$。即：
  $$V_{\ast }(s)=max(\mathcal{V})$$
• 定义2：
  在当前时刻状态$S_t=s$的情况下，我们的策略$\pi (a\mid s)$依然是有穷的，我们将所有可能出现的策略全部收集起来，产生一个关于策略$\pi$的集合：
  $$\Pi =\{{\pi }^{(1)},{\pi }^{(2)},{\pi }^{(3)},...\}$$
  我们从该集合中选择一个策略${\pi }^{\ast }$，使得它对应的状态价值函数最大。结合定义1中的设定，即：
  $$V_{{\pi }^{\ast }}(s)=max(\mathcal{V})$$

将2个定义进行合并，我们可以得到：
$$V_{\ast }(s)=V_{{\pi }^{\ast }}(s)$$
虽然两者都表示最优状态价值函数，但是对应的定义却不同；

最优状态-动作价值函数

上述两种类型的定义同样适用于最优动作-状态价值函数的选择上。设最优策略为${\pi }^{\circ }$，即：
$$q_{\ast }(s,a)=q_{{\pi }^{\circ }}(s,a)=max(\mathcal{Q})$$
其中$\mathcal{Q}$表示关于状态动作价值函数$q_{\pi }(s,a)$的集合。
$$\mathcal{Q}=\{q_{{\pi }^{(1)}}(s,a),q_{{\pi }^{(2)}}(s,a),q_{{\pi }^{(3)}}(s,a),...\}$$

小小的题外话 - 最大值/期望值

我们对期望(expectation)是非常了解的，已知一组数值集合和每个数值对应的权重，我们很容易算出这组数值集合的期望值。
本质上，期望值就是输出值的加权和。
而最大值(The maximum value)我们就更熟悉了，它就是已知的数据中最大的一个值。

最大值和期望值之间的大小关系

如果我们将权重看成概率的话，实际上，选择最大值同样是存在概率分布的。只不过这个概率分布比较特殊：
假设数值集合$X$包含3个元素：
$$X=\{3,4,5\}$$
并且赋予3个元素不同的权重：

元素(element)	权重(weight)
3	0.2
4	0.4
5	0.4

我们很容易计算出$X$的期望：
$$E(X)=3\times 0.2+4\times 0.4+5\times 0.4=4.2$$
如果改成选择数值集合$X$内的最大值，这个“选择最大值”的任务自动赋予3个元素各自的权重：

元素(element)	权重(weight)
3	0.0
4	0.0
5	1.0

我们发现：选择最大值的权重分布只包含$\{0,1\}$ 2种权重。结合上述赋予的权重，来计算$X$的最大值：
$$max(X)=3\times 0.0+4\times 0.0+5\times 1.0=5$$
我们从上述示例中发现：期望值 < 最大值。
这种情况是否会一直都成立？从逻辑上讲，在分配权重的时候,但凡我们给非最大值赋予了一些权重，势必会对应减少最大值的权重。
从常规上来讲，期望值总是小于最大值的。但也存在特殊情况：

• 数值集合$X$中所有元素均相同；
• 将全部的权重(weight)赋予最大值；

上述2种情况的期望值 = 最大值。
综上，根据逻辑(不严谨)，我们可以得出：在数值集合确定的情况下，期望值$E(X)⩽$ 最大值$max(X)$。

最优策略与两种价值函数间的关系

根据上一节介绍的$V_{\pi }(s)$和$q_{\pi }(s,a)$之间的关联关系：
$$V_{\pi }(s)=\pi (a\mid s)q_{\pi }(s,a)$$
我们将${\pi }^{\ast }$替换$\pi$：
$$V_{{\pi }^{\ast }}(s)={\pi }_{\ast }(a\mid s)q_{{\pi }^{\ast }}(s,a)$$
我们知道$V_{{\pi }^{\ast }}(s)$是最大状态价值函数，${\pi }_{\ast }(a\mid s)$是最优策略。结合上面$\to$最大值选择的权重分布，最优策略内部权重分布遵循如下规则：
$${\pi }_{\ast }(a\mid s)=\{\begin{array}{l}1ifa=\underset{a\in \mathcal{A}}{\mathrm{argmax}}{q}_{{\pi }^{\ast }}(s,a)\\ 0else\end{array}$$
现在知道，我们的最优策略${\pi }^{\ast }$只包含$\{0,1\}$两种权重，那么${\pi }^{\ast }$中权重1对应的值必然是最优状态-动作价值函数，即：
$$q_{{\pi }^{\ast }}(s,a)=q_{\ast }(s,a)=q_{{\pi }^{\circ }}(s,a)$$
根据上述的逻辑推演，我们最终得到2条结论：

• 最优状态价值函数$V_{{\pi }^{\ast }}(s)$和最优状态-动作价值函数$q_{{\pi }^{\ast }}(s,a)$中的最优策略${\pi }_{\ast }$是同一个策略。
• $$\begin{array}{rl}{V}_{{\pi }^{\ast }}(s)& ={\pi }_{\ast }(a\mid s)q_{{\pi }^{\ast }}(s,a)\\ & =\underset{a}{\max }{q}_{{\pi }^{\ast }}(s,a)\end{array}$$
  $$\to V_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$
  上式表示$V_{\ast }(s)\to q_{\ast }(s,a)$的关联关系，反之同理，后续只需要保证它们是最优策略即可。
  $$q_{\ast }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r\mid s,a)[r+\gamma V_{\ast }(s^{\prime })]$$

贝尔曼最优方程表达式

根据上面的关联关系，我们继续执行套娃模式：

• $$\begin{array}{rl}{V}_{\ast }(s)& =\underset{a}{\max }{q}_{\ast }(s,a)\\ & =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r\mid s,a)[r+\gamma V_{\ast }(s^{\prime })]\end{array}$$
• $$\begin{array}{rl}{q}_{\ast }(s,a)& =\sum _{s^{\prime },r}p(s^{\prime },r\mid s,a)[r+\gamma V_{\ast }(s^{\prime })]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r\mid s,a)[r+\gamma \underset{a}{\max }{q}_{\ast }(s,a)]\end{array}$$

贝尔曼最优方程的逻辑过程推导完毕。

相关参考：
【强化学习】马尔科夫决策过程【白板推导系列】
刘建平 - 强化学习（二）马尔科夫决策过程(MDP)