二分图判定&二分图最大匹配模板
二分图定义
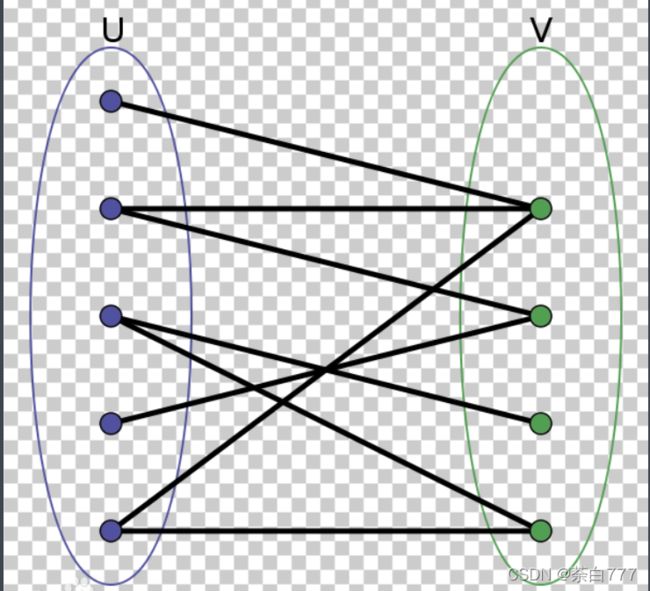
可以把所有的点划分成两个集合,集合内部不存在边,集合之间存在边;
01染色判定二分图
性质
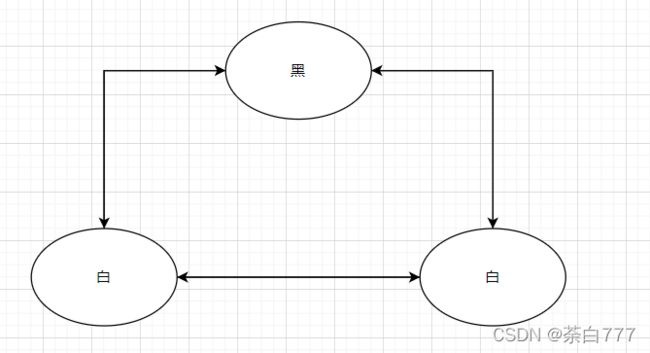
- 一个图是二分图等价于不存在奇数环
奇数环是指点的个数是奇数的环,如下图;
有一个通俗的解释,奇数个点无法被两种颜色均分;
那么我们的做法很简单,如果一个点没有被染色,那么我们将它(记为 u u u)染为白色,将与 u u u相连的点染成黑色;
不断重复这个过程即可,若过程中发现同色相连,那么就产生矛盾了;
染色法判二分图
传送门
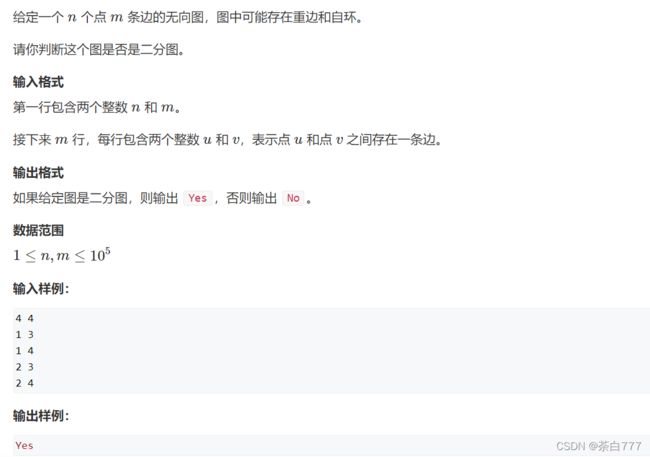
题面
时间复杂度
O ( N + M ) , N 为 点 的 个 数 , M 为 边 的 个 数 O(N+M),N为点的个数,M为边的个数 O(N+M),N为点的个数,M为边的个数
Code
#include 匈牙利算法
用于求解二分图的最大的成功匹配;
成功匹配指的是,两个点一一配对,不存在脚踩多条船的情况;
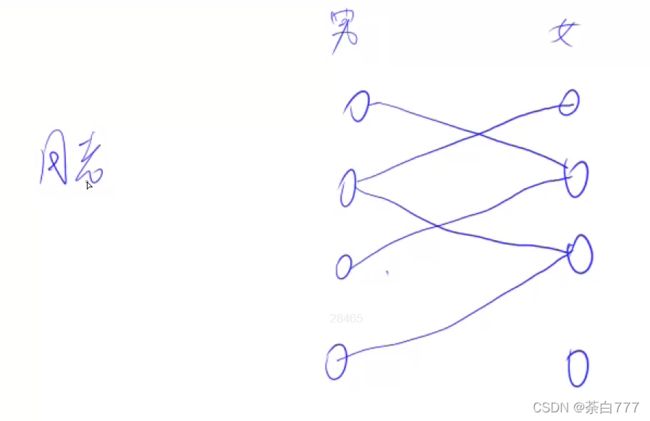
也可以称为,月老算法;
比如我们是月老,问我们最多能给多少对男女牵红线(一夫一妻!!!);
算法过程是这样的,如果一个点可以匹配另一个点,那么我们直接匹配,皆大欢喜;
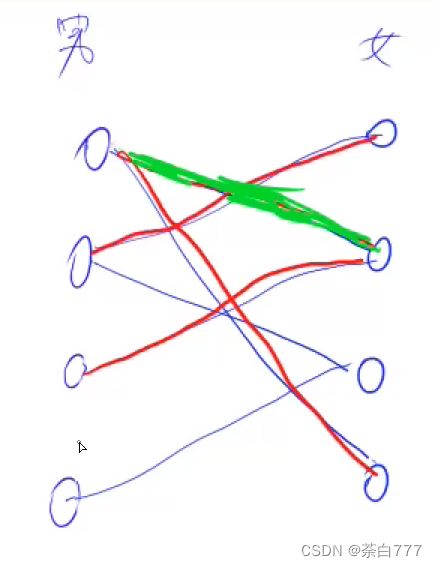
如果不能匹配,比如说 u u u的心仪对象是 v v v,但是 v v v已经和 w w w配对了;那么 u u u就会尝试把 w w w绿了,但是绿的前提是 w w w能找到另外的新欢,比如说 k k k;
那么 u , v u,v u,v配对, w , k w,k w,k配对;
比如说下图的左三就绿了左一,抢了右二…(NTR)
二分图的最大匹配
题面
时间复杂度
O ( N ∗ M ) , N 为 点 数 , M 为 边 数 O(N*M),N为点数,M为边数 O(N∗M),N为点数,M为边数,实际时间没有这么大;
Code
注意一个地方,虽然二分图是无向图,但是我们这里存图只用存左边到右边,因为只用到了左边到右边;
#include