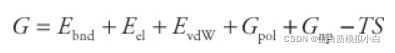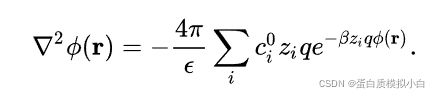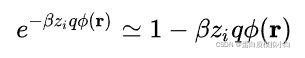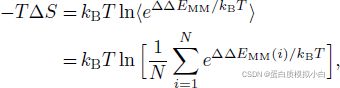分子动力学模拟自由能计算gmx_mmpbsa脚本原理和使用
先讲原理:
前三项是标准的键能项(MM,包括键,角,和二面角的变化引起的能量变化、库伦势、范德瓦尔斯相互作用),Gpol和Gnp是溶剂化自由能的极性和非极性贡献。Gpol通常通过求解PB方程或使用广义Born(GB)模型获得,而非极性项通过与溶剂可及表面积(SASA)的线性关系进行估计。最后一项是绝对温度T乘以熵S,通过振动频率的正常模式分析进行估计。
Gpol
周围的水,电解质会对盒子内的蛋白质原子电荷做出反应,涉及到的就是溶剂的极性部分贡献。
泊松-玻尔兹曼方程 (英语:Poisson- Boltzmann Equation)是用来计算电解质溶液中离子浓度和电荷密度分布的一个微分方程。PB方程长这样,求解方程可以得到溶剂对蛋白质分子的自由能贡献的极性部分。
是一个非线性偏微分方程,很难解,一般采用数值解法,APBS就是可以解这个方程的软件。
近似解法是在稀溶液中,进行下面展开近似,
得到德拜-休克尔方程
是线性方程,更容易解。所以在稀溶液中,德拜-休克尔方程对于泊松-玻尔兹曼方程而言是很好的近似。
个人理解影响这一部分主要的参数为带电量、蛋白质形成的表面,表面原子的大小。
这部分的结果会有很大的不准确性。
Gnpol
Nonpolar solvation energy,非极性溶剂化能,包括了溶剂和溶质之间的排斥力和引力。
SASA-Only Nonpolar Model 是使用最广泛的非极性模型之一,溶剂可达表面积(SASA)模型基于SASA线性依赖于非极性项的假设,因此可以进行如下计算:
Gnpol = γA+b
其中A为SASA,b,γ为参数。
影响这一部分的主要是蛋白质的表面积。
MM
可以查看上篇。键能主要是原子的距离,库伦势主要是原子的距离和电荷量、介电常数。
计算过程中,多次短时间的模拟会带来更好的收敛效果(单个长期模拟会低估结果的不确定性)。
对于抗生物素蛋白,需要20-50次模拟才能给出七种生物素类似物1 kJ/mol的标准误差(每个配体总共模拟6-15 ns)。
PB结果强烈依赖于所采用的半径。
熵:
-TΔS
影响结果的因素:力场、电解质常数、选取的轨迹时间。
gmx_mmpbsa 脚本使用:
针对linux系统,模拟完计算结合自由能
1.下载地址:gmxtool (jerkwin.github.io)
下载gmx_mmpbsa.bsh
2.APBS软件安装
Releases · Electrostatics/apbs · GitHub
2.1这个网站下载APBS二进制包,推荐下载1.4或者1.5的,最新版本可能使用会有问题。
2.2下载后移到linux文件目录下,可以放到软件安装位置。
2.3解压安装包
tar -xvf APBS-1.5-linux64
cd APBS-1.5-linux64
pwd (获取安装位置,后面添加环境变量)
2.4 添加环境变量
vim ~/.bashrc
export LD_LIBRARY_PATH=`pwd`/lib:${LD_LIBRARY_PATH}
export PATH=`pwd`/bin:${PATH}
添加最下面这两行中间是刚才的安装位置,后面的lib和bin不要忘了。
然后保存。
3.脚本使用
3.1.先改apbs位置,找到下图位置,改为刚才安装apbs的位置(path)/bin/apbs
忘了的话也可以使用命令whereis apbs也会出来路径。
把不用的行注释掉。
3.2.使用的时候把这个文件放到模拟完的含有md.xtc md.tpr index.ndx(或者md.gro)的文件夹下
修改输入参数,可以两种方法,直接在脚本里改,或者运行脚本的时候在后面传参。
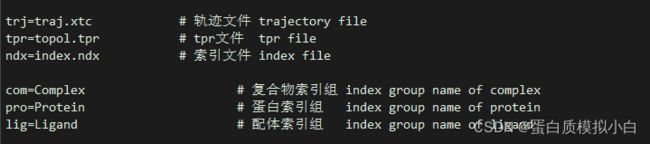
将后面的改为自己的文件名和组名。
或者 按文件开头写的进行运行
bash gmx_mmpbsa -f traj.xtc -s topol.tpr -n index.ndx -com Complex -pro Protein -lig Ligand -ts ie
(建议将Protein改为其他名字,因为gromacs自带分组就有Protein,容易冲突。例如我习惯pro=Chain_A
lig=Chain_B
com=Complex
trj=md.xtc
tpr=md.tpr
ndx=index.ndx
)
如果要修改使用轨迹的时间 可以直接修改脚本第81行(图中最下面一行,dt是间隔时间,缩小的话可以增加帧数,-b 开始时间 -e 结束时间)
3.3.分组
gmx make_ndx -f md.gro
使用gromacs命令进行分组这里注意 r 和 ri 的区别
运行以上命令后 输入 l 会列出所有残基,前面的序号就可以用 ri 进行选择 r 选择的是gro文件里有的序号,如果有重复的残基序号的话容易选错。推荐使用 ri
4 运行计算
./gmx_mmpbsa
就行。或者输入要修改的参数
5.结果分析
自由能数据文件在 _pid~MMPBSA.dat 里,
文件上面的是每一帧的分解项,有原理部分提到的各种分解项,with DH 是德拜-休克尔修正项,当体系带有较大的电荷时,需要使用括号里修正后的数据,体系电荷不大的话两者数据相差不会太大。
_pid~res_MMPBSA.dat
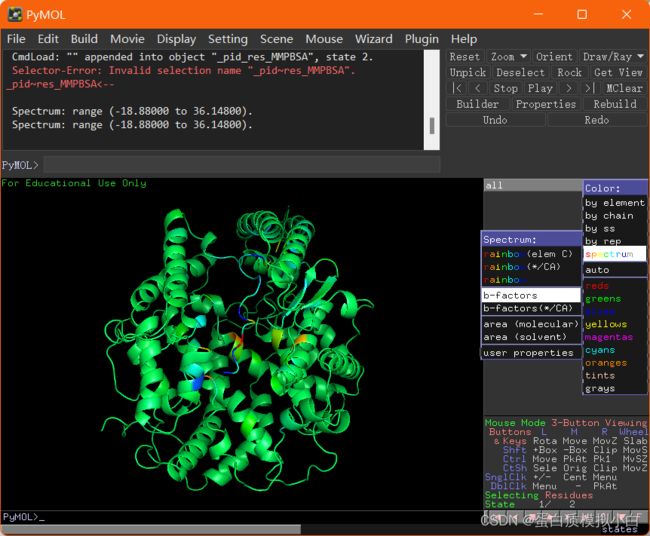
能量的残基分解数据,可以做残基能量分解图。
残基能量分解写入pdb文件,可以直接用pymol或者VDM打开。
着色方式选择β-factor可以看到残基的能量分布。
个人经验(可能不对。欢迎交流):
1. 使用挺简单的,但最后的结果可重复性比较差,进行重复的模拟后重复的计算,两次之间可能会差很多。文献的建议是多次短时间模拟取平均值(例如20次1ns模拟),不同力场的效果也差距很大,对于基于较短MD模拟(1ns)的MM/PBSA计算,ff03力场也是一个不错的选择。
2. 计算出来的自由能数据可能会很离谱,确保分组和其他操作没问题的话还是需要反复调参数和查文献搞定。
3. 取的帧数对结果影响很大,文献里有1ns时长取了10000帧的。。。emm多看看文献看看相似的体系怎么取的。
4. 大部分的文献反映出这个方法计算的自由能数据和实验差距可能会很大,甚至可能次序完全不对。所以还是要根据体系进行原理调整。(不是指这个脚本,指的是MMPBSA这个方法)
参考文献:
The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities,2015
gmxtool (jerkwin.github.io)
Assessing the Performance of MM/PBSA and MM/GBSA Methods. 3. The Impact of Force Fields and Ligand Charge Models,2013