《ADVENT:Adversarial Entropy Minimization for Domain Adaptation in Semantic Segmentation》论文笔记
参考代码:ADVENT
1. 概述
导读:由于在训练场景和测试场景存在偏差(domain-shift),因而就会使得训练场景(source域)下的精度在测试场景(target域)下下降的问题。这篇文章针对分割场景下的domain adaptation问题提出在像素预测结果上使用基于熵的损失,既是文章为domain adaptation提出两种损失:entropy loss和GAN的对抗损失,从而降低文章提出的target图像的熵值。
从source域到target域的切换会存在性能的损失,那么这个损失的表现形式是什么呢?文章对此引出了熵的概念,从source到target的分割结果可以从图1中看出是一个熵增的状态。

从target的分割结果中存在较多的噪声/置信度不高的情况,看作为一个高熵体。因而就可以通过熵损失的形式降低target输出结果的熵值,从而达到提升分割性能的目地。具体在文章中,是使用在独立像素预测的结果熵使用熵损失进行约束,降低预测结果的熵值,并且从全局上进行source域和target域的分布拟合。
2. 方法设计
文章提出的网络结构是在分割网络的基础上额外添加domain adaptation分支得到的,其网络结构见下图所示:
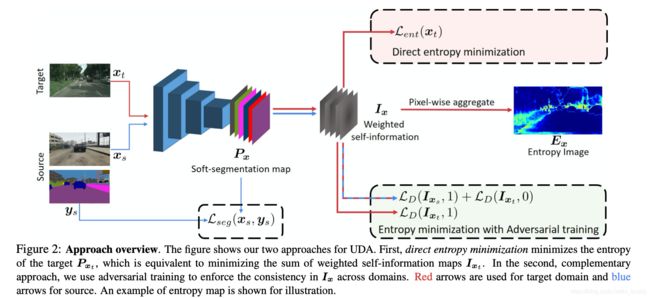
2.1 分割部分的损失
设输入source域的图像为 x s ∈ R ( H ∗ W ∗ 3 ) x_s\in R^{(H*W*3)} xs∈R(H∗W∗3),对应的one-hot标注为 y s = [ y s ( h , w , c ) ] c y_s=[ y_s^{(h,w,c)}]_c ys=[ys(h,w,c)]c,则经过分割网络之后得到分割结果 P s = [ P x ( h , w , c ) ] ( h , w , c ) P_s=[P_x^{(h,w,c)}]_{(h,w,c)} Ps=[Px(h,w,c)](h,w,c),则对应的损失函数定义为:
L s e g ( x s , y s ) = − ∑ h = 1 H ∑ w = 1 W ∑ c = 1 C y s ( h , w , c ) l o g P s ( h , w , c ) L_{seg}(x_s,y_s)=-\sum_{h=1}^H\sum_{w=1}^W\sum_{c=1}^Cy_s^{(h,w,c)}logP_s^{(h,w,c)} Lseg(xs,ys)=−h=1∑Hw=1∑Wc=1∑Cys(h,w,c)logPs(h,w,c)
对应的需要优化的网络参数:
min θ F 1 ∣ x s ∣ ∑ x s L s e g ( x s , y s ) \min_{\theta_F}\frac{1}{|x_s|}\sum_{x_s}L_{seg}(x_s,y_s) θFmin∣xs∣1xs∑Lseg(xs,ys)
2.2 target分割结果熵损失
由于target数据是不存在真实的监督标签的,因而这里采用的是伤损失的形式,因而在 ( h , w ) (h,w) (h,w)平面上其熵值 E x t ∈ [ 0 , 1 ] ( H ∗ W ) E_{x_t}\in[0,1]^{(H*W)} Ext∈[0,1](H∗W)计算表示为:
E x t ( h , w ) = − 1 l o g ( C ) ∑ c = 1 C P t ( h , w , c ) l o g P t ( h , w , c ) E_{x_t}^{(h,w)}=\frac{-1}{log(C)}\sum_{c=1}^CP_t^{(h,w,c)}logP_t^{(h,w,c)} Ext(h,w)=log(C)−1c=1∑CPt(h,w,c)logPt(h,w,c)
其对应的损失函数描述为:
L e n t ( x t ) = ∑ ( h , w ) E x t ( h , w ) L_{ent}(x_t)=\sum_{(h,w)}E_{x_t}^{(h,w)} Lent(xt)=(h,w)∑Ext(h,w)
加上熵之后的网络参数优化描述为( λ e n t = 1 e − 3 \lambda_{ent}=1e-3 λent=1e−3):
min θ F 1 ∣ x s ∣ ∑ x s L s e g ( x s , y s ) + λ e n t ∣ x t ∣ ∑ x t L e n t ( x t ) \min_{\theta_F}\frac{1}{|x_s|}\sum_{x_s}L_{seg}(x_s,y_s)+\frac{\lambda_{ent}}{|x_t|}\sum_{x_t}L_{ent}(x_t) θFmin∣xs∣1xs∑Lseg(xs,ys)+∣xt∣λentxt∑Lent(xt)
与self-training(ST)的联系:
在ST中会按照一个固定的数值或是阈值比例选择一些较高置信度的点 K K K作为预测的标签 y t ^ \hat{y_t} yt^,这里的标签是使用target数据去预测并选取出来的,因而这部分的损失函数描述为:
L s e g ( x , y t ^ ) = − ∑ ( h , w ) ∈ K ∑ c = 1 C y t ^ ( h , w , c ) l o g P t ( h , w , c ) L_{seg}(x,\hat{y_t})=-\sum_{(h,w)\in K}\sum_{c=1}^C\hat{y_t}^{(h,w,c)}logP_t^{(h,w,c)} Lseg(x,yt^)=−(h,w)∈K∑c=1∑Cyt^(h,w,c)logPt(h,w,c)
因而加上这部分的损失函数,有监督的分割部分优化过程可以描述为:
min θ F 1 ∣ x s ∣ ∑ x s L s e g ( x s , y s ) + λ p l ∣ x t ∣ ∑ x t L s e g ( x t , y t ^ ) \min_{\theta_F}\frac{1}{|x_s|}\sum_{x_s}L_{seg}(x_s,y_s)+\frac{\lambda_{pl}}{|x_t|}\sum_{x_t}L_{seg}(x_t,\hat{y_t}) θFmin∣xs∣1xs∑Lseg(xs,ys)+∣xt∣λplxt∑Lseg(xt,yt^)
2.3 基于GAN的熵最小化
文章从熵的角度去优化source和target之间的gap,对于GAN网络部分的输入其定义为:
I x ( h , w ) = − P x ( h , w ) l o g x ( h , w ) I_x^{(h,w)}=-P_x^{(h,w)}log_x^{(h,w)} Ix(h,w)=−Px(h,w)logx(h,w)
则这里首先优化的vGAN部分的优化可以描述为:
min θ D 1 ∣ x s ∣ ∑ x s L D ( I x s , 1 ) + 1 ∣ x t ∣ ∑ x t ( I x t , 0 ) \min_{\theta_D}\frac{1}{|x_s|}\sum_{x_s}L_D(I_{x_s},1)+\frac{1}{|x_t|}\sum_{x_t}(I_{x_t},0) θDmin∣xs∣1xs∑LD(Ixs,1)+∣xt∣1xt∑(Ixt,0)
之后对于分割网络部分优化描述为
min θ F 1 ∣ x t ∣ ∑ x t L D ( I x t , 1 ) \min_{\theta_F}\frac{1}{|x_t|}\sum_{x_t}L_D(I_{x_t},1) θFmin∣xt∣1xt∑LD(Ixt,1)
因而,整个网络的优化任务可以描述为( λ a d v = 1 e − 3 \lambda_{adv}=1e-3 λadv=1e−3):
min θ F 1 ∣ x s ∣ ∑ x s L s e g ( x s , y s ) + λ a d v ∣ x t ∣ ∑ x t L D ( I x t , 1 ) \min_{\theta_F}\frac{1}{|x_s|}\sum_{x_s}L_{seg}(x_s,y_s)+\frac{\lambda_{adv}}{|x_t|}\sum_{x_t}L_D(I_{x_t},1) θFmin∣xs∣1xs∑Lseg(xs,ys)+∣xt∣λadvxt∑LD(Ixt,1)
2.4 类间不平衡问题
为了解决类间不平衡的问题,文章通过统计source数据中的类别分布构建类间分布先验 p s p_s ps,从而去调配损失函数,则经过类别先验调配之后的损失target损失描述为:
L c p ( x t ) = ∑ c = 1 C m a x ( 0 , μ P s c − E c ( P x t c ) ) L_{cp}(x_t)=\sum_{c=1}^Cmax(0,\mu P_s^c-E_c(P_{x_t}^c)) Lcp(xt)=c=1∑Cmax(0,μPsc−Ec(Pxtc))
其中, μ ∈ [ 0 , 1 ] \mu \in[0,1] μ∈[0,1]是松弛系数系数,用以处理那些单张target图像中真实分布与source中 p s p_s ps相差较大的情况。

