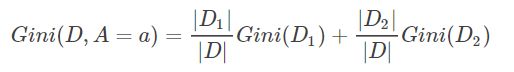《机器学习实战》学习笔记(二):决策树
目录
- 一、决策树
-
- 1.1 决策树简介
- 1.2 使用决策树的过程
- 二、ID3算法
-
- 2.1 算法流程
- 2.2 算法原理
-
- 2.2.1 信息熵
- 2.2.2 信息增益
- 2.3 算法实例
-
- 2.3.1 实例背景
- 2.3.2 数据处理:
- 2.3.3 计算信息熵并划分数据集
- 2.3.4 计算信息增益以选择最好特征
- 2.3.5 处理叶子结点——多数表决法
- 2.3.6 建立决策树
- 三、C4.5算法
-
- 3.1 算法流程
- 3.2 算法原理
- 3.3 算法实例
-
- 3.3.1 计算信息增益率以选择最好特征
- 3.3.2 建立决策树
- 四、CART算法
-
- 4.1 算法流程
- 4.2 算法原理
- 4.3 基尼指数
-
- 4.4 算法实例
- 4.4.1 计算基尼指数以选择最好特征
- 4.4.2 建立决策树
- 五、决策树剪枝
-
- 5.1 算法目的
- 5.2 算法思路
- 5.3 剪枝类型
-
- 5.3.1 预剪枝
- 5.3.2 后剪枝
- 5.3.3 两种剪枝对比
- 六、实验结果
-
- 6.1 绘制决策树
- 6.2 main.py
- 6.3 ID3决策树
- 6.4 C4.5决策树
- 6.5 CART决策树
- 七、实验总结
一、决策树
1.1 决策树简介
决策树是什么?决策树(decision tree)是一种基本的分类与回归方法。举个通俗易懂的例子,如下图所示的流程图就是一个决策树,长方形代表判断模块(decision block),椭圆形成代表终止模块(terminating block),表示已经得出结论,可以终止运行。从判断模块引出的左右箭头称作为分支(branch),它可以达到另一个判断模块或者终止模块。我们还可以这样理解,分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。如下图所示的决策树,长方形和椭圆形都是结点。长方形的结点属于内部结点,椭圆形的结点属于叶结点,从结点引出的左右箭头就是有向边。而最上面的结点就是决策树的根结点(root node)。这样,结点说法就与模块说法便对应了。
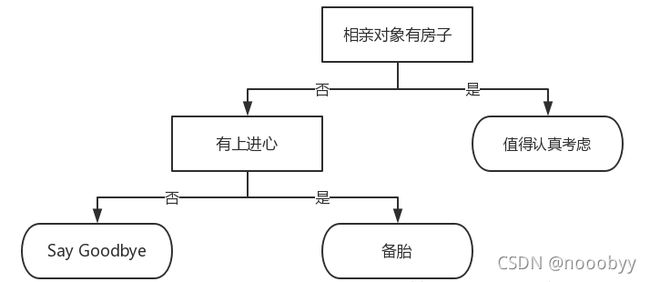
由实验一中的约会网站匹配进行延伸,可以得到上图所示的流程图——相亲对象分类系统。它首先检测相亲对方是否有房。如果有房,则对于这个相亲对象可以考虑进一步接触。如果没有房,则观察相亲对象是否有上进心,如果没有,直接Say Goodbye。
不过这只是个简单的相亲对象分类系统,只是做了简单的分类。真实情况可能要复杂得多,考虑因素也可以是五花八门。脾气好吗?会做饭吗?愿意做家务吗?家里几个孩子?父母做什么?
我们可以把决策树看成一个if-then规则的集合,将决策树转换成if-then规则的过程是这样的:由决策树的根结点(root node)到叶结点(leaf node)的每一条路径构建一条规则;路径上内部结点的特征对应着规则的条件,而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质:互斥并且完备。这就是说,每一个实例都被一条路径或一条规则所覆盖,而且只被一条路径或一条规则所覆盖。这里所覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。
由此可以看出,决策树的基本思想,实际上就是寻找最纯净的划分方法,这个最纯净在数学上称为纯度,纯度通俗点理解就是目标变量要分得足够开;另一种理解是分类误差率的一种衡量。实际决策树算法往往用到的是,纯度的另一面也即不纯度,下面是不纯度的公式。不纯度的选取有多种方法,每种方法也就形成了不同的决策树方法,比如ID3算法使用信息增益作为不纯度;C4.5算法使用信息增益率作为不纯度;CART算法使用基尼系数作为不纯度,接下来将通过实例分别实现这三种算法。
1.2 使用决策树的过程
使用决策树做预测需要以下过程:
- 收集数据:可以使用任何方法。比如想构建一个相亲系统,我们可以从媒婆那里,或者通过参访相亲对象获取数据。根据他们考虑的因素和最终的选择结果,就可以得到一些供我们利用的数据了
- 准备数据:收集完的数据,我们要进行整理,将这些所有收集的信息按照一定规则整理出来,并排版,方便我们进行后续处理
- 分析数据:可以使用任何方法,决策树构造完成之后,我们可以检查决策树图形是否符合预期
- 训练算法:这个过程也就是构造决策树,同样也可以说是决策树学习,就是构造一个决策树的数据结构
- 测试算法:使用经验树计算错误率。当错误率达到了可接收范围,这个决策树便可以使用
- 使用算法:此步骤可以使用适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义
二、ID3算法
2.1 算法流程
基本的ID3 算法通过自顶向下构造决策树来进行学习。
构造过程是从“哪一个属性将在树的根结点被测试?”这个问题开始的。
为了回答这个问题,使用统计测试来确定每一个实例属性单独分类训练样例的能力。
(1)分类能力最好的属性被选作树的根结点的测试。
(2)然后为根结点属性的每个可能值产生一个分支,并把训练样例排列到适当的分支(也就是,样例的该属性值对应的分支)之下。
(3)然后重复整个过程,用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。
这形成了对合格决策树的贪婪搜索(greedy search ),也就是算法从不回溯重新考虑以前的选择。

2.2 算法原理
ID3用以给一个数据集创建决策树,该算法是以信息论为基础,以信息熵和信息增益为衡量标准,从而实现对数据的归纳分类。
2.2.1 信息熵
熵这个概念最早起源于物理学,在物理学中是用来度量一个热力学系统的无序程度,而在信息学里面,熵是对不确定性的度量。在1948年,香农引入了信息熵(information entropy),将其定义为离散随机事件出现的概率,一个系统越是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
对于有K个类别的分类问题来说,假定样本集合D中第 k 类样本所占的比例为pkpk(k=1,2,…,Kk=1,2,…,K),则样本集合D的信息熵定义为:
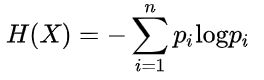
2.2.2 信息增益
在决策树的分类问题中,信息增益(information gain)是针对一个特定的分支标准(branching criteria)T,计算原有数据的信息熵与引入该分支标准后的信息熵之差。信息增益的定义如下:
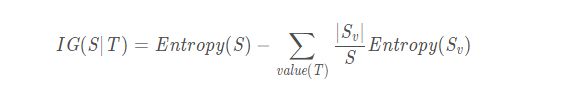
其中a是有V个不同取值的离散特征,使用特征a对样本集D进行划分会产生V个分支, DvDv表示D中所有在特征a上取值为 avav的样本,即第v个分支的节点集合。 |Dv||D||Dv||D|表示分支节点的权重,即分支节点的样本数越多,其影响越大。
ID3会为每一个属性计算信息熵,具有最大信息增益的属性在本次迭代中用来划分数据集X。
2.3 算法实例
2.3.1 实例背景
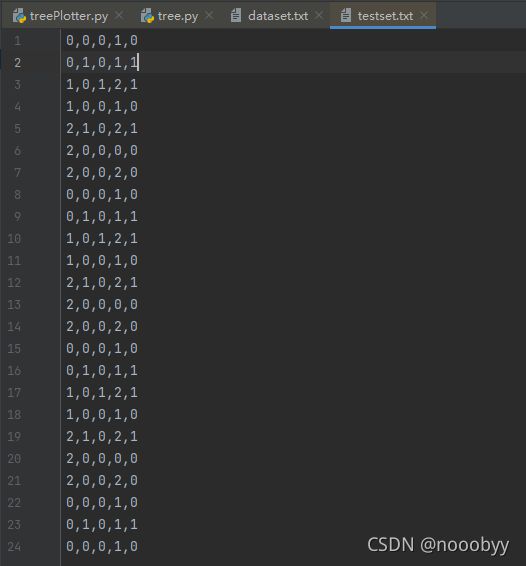
通常我们在申请贷款时,银行会根据每个人的一些信用指标,判断其是否具有还款能力,从而决定贷款的成功与否。
2.3.2 数据处理:
取数据集的80%作为训练集,训练集数据如下:
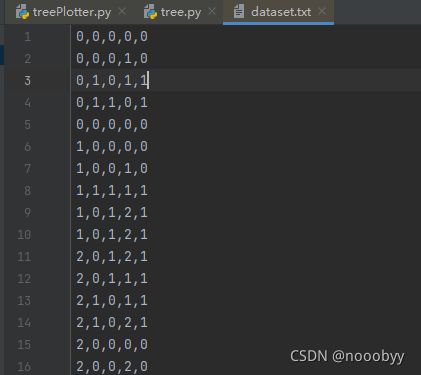
现在通过所给的训练数据数据学习一个贷款申请的决策树,用以对未来的贷款申请进行分类,即当新的客户提出贷款申请时,根据申请人的特征利用决策树决定是否批准贷款申请。训练数据给出了年龄、有工作、有自己的房子、信贷情况共四个特征,究竟选择哪个特征更好些?直观上,如果一个特征具有更好的分类能力,那么就更应该选择这个特征,此时便可以利用ID3算法使用信息增益作为分类准测。
def read_dataset(filename):
"""
年龄段:0代表青年,1代表中年,2代表老年;
有工作:0代表否,1代表是;
有自己的房子:0代表否,1代表是;
信贷情况:0代表一般,1代表好,2代表非常好;
类别(是否给贷款):0代表否,1代表是
"""
fr = open(filename, 'r')
all_lines = fr.readlines() # list形式,每行为1个str
# print all_lines
labels = ['年龄段', '有工作', '有自己的房子', '信贷情况']
# featname=all_lines[0].strip().split(',') #list形式
# featname=featname[:-1]
labelCounts = {}
dataset = []
for line in all_lines[0:]:
line = line.strip().split(',') # 以逗号为分割符拆分列表
dataset.append(line)
return dataset, labels
def read_testset(testfile):
"""
年龄段:0代表青年,1代表中年,2代表老年;
有工作:0代表否,1代表是;
有自己的房子:0代表否,1代表是;
信贷情况:0代表一般,1代表好,2代表非常好;
类别(是否给贷款):0代表否,1代表是
"""
fr = open(testfile, 'r')
all_lines = fr.readlines()
testset = []
for line in all_lines[0:]:
line = line.strip().split(',') # 以逗号为分割符拆分列表
testset.append(line)
return testset
2.3.3 计算信息熵并划分数据集
# 计算信息熵
def cal_entropy(dataset):
numEntries = len(dataset)
labelCounts = {}
# 给所有可能分类创建字典
for featVec in dataset:
currentlabel = featVec[-1]
if currentlabel not in labelCounts.keys():
labelCounts[currentlabel] = 0
labelCounts[currentlabel] += 1
Ent = 0.0
for key in labelCounts:
p = float(labelCounts[key]) / numEntries
Ent = Ent - p * log(p, 2) # 以2为底求对数
return Ent
# 划分数据集
def splitdataset(dataset, axis, value):
retdataset = [] # 创建返回的数据集列表
for featVec in dataset: # 抽取符合划分特征的值
if featVec[axis] == value:
reducedfeatVec = featVec[:axis] # 去掉axis特征
reducedfeatVec.extend(featVec[axis + 1:]) # 将符合条件的特征添加到返回的数据集列表
retdataset.append(reducedfeatVec)
return retdataset
2.3.4 计算信息增益以选择最好特征
def ID3_chooseBestFeatureToSplit(dataset):
numFeatures = len(dataset[0]) - 1
baseEnt = cal_entropy(dataset)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures): # 遍历所有特征
# for example in dataset:
# featList=example[i]
featList = [example[i] for example in dataset]
uniqueVals = set(featList) # 将特征列表创建成为set集合,元素不可重复。创建唯一的分类标签列表
newEnt = 0.0
for value in uniqueVals: # 计算每种划分方式的信息熵
subdataset = splitdataset(dataset, i, value)
p = len(subdataset) / float(len(dataset))
newEnt += p * cal_entropy(subdataset)
infoGain = baseEnt - newEnt
print(u"ID3中第%d个特征的信息增益为:%.3f" % (i, infoGain))
if (infoGain > bestInfoGain):
bestInfoGain = infoGain # 计算最好的信息增益
bestFeature = i
return bestFeature
2.3.5 处理叶子结点——多数表决法
def majorityCnt(classList):
'''
数据集已经处理了所有属性,但是类标签依然不是唯一的,
此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决定该叶子节点的分类
'''
classCont = {}
for vote in classList:
if vote not in classCont.keys():
classCont[vote] = 0
classCont[vote] += 1
sortedClassCont = sorted(classCont.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCont[0][0]
2.3.6 建立决策树
def ID3_createTree(dataset, labels, test_dataset):
classList = [example[-1] for example in dataset]
if classList.count(classList[0]) == len(classList):
# 类别完全相同,停止划分
return classList[0]
if len(dataset[0]) == 1:
# 遍历完所有特征时返回出现次数最多的
return majorityCnt(classList)
bestFeat = ID3_chooseBestFeatureToSplit(dataset)
bestFeatLabel = labels[bestFeat]
print(u"此时最优索引为:" + (bestFeatLabel))
ID3Tree = {bestFeatLabel: {}}
del (labels[bestFeat])
# 得到列表包括节点所有的属性值
featValues = [example[bestFeat] for example in dataset]
uniqueVals = set(featValues)
if pre_pruning:
ans = []
for index in range(len(test_dataset)):
ans.append(test_dataset[index][-1])
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
root_acc = cal_acc(test_output=[leaf_output] * len(test_dataset), label=ans)
outputs = []
ans = []
for value in uniqueVals:
cut_testset = splitdataset(test_dataset, bestFeat, value)
cut_dataset = splitdataset(dataset, bestFeat, value)
for vec in cut_testset:
ans.append(vec[-1])
result_counter = Counter()
for vec in cut_dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
outputs += [leaf_output] * len(cut_testset)
cut_acc = cal_acc(test_output=outputs, label=ans)
if cut_acc <= root_acc:
return leaf_output
for value in uniqueVals:
subLabels = labels[:]
ID3Tree[bestFeatLabel][value] = ID3_createTree(
splitdataset(dataset, bestFeat, value),
subLabels,
splitdataset(test_dataset, bestFeat, value))
if post_pruning:
tree_output = classifytest(ID3Tree,
featLabels=['年龄段', '有工作', '有自己的房子', '信贷情况'],
testDataSet=test_dataset)
ans = []
for vec in test_dataset:
ans.append(vec[-1])
root_acc = cal_acc(tree_output, ans)
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
cut_acc = cal_acc([leaf_output] * len(test_dataset), ans)
if cut_acc >= root_acc:
return leaf_output
return ID3Tree
三、C4.5算法
3.1 算法流程
C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习:给定一个数据集,其中的每一个元组都能用一组属性值来描述,每一个元组属于一个互斥的类别中的某一类。C4.5的目标是通过学习,找到一个从属性值到类别的映射关系,并且这个映射能用于对新的类别未知的实体进行分类。
C4.5由J.Ross Quinlan在ID3的基础上提出的。ID3算法用来构造决策树。决策树是一种类似流程图的树结构,其中每个内部节点(非树叶节点)表示在一个属性上的测试,每个分枝代表一个测试输出,而每个树叶节点存放一个类标号。一旦建立好了决策树,对于一个未给定类标号的元组,跟踪一条有根节点到叶节点的路径,该叶节点就存放着该元组的预测。决策树的优势在于不需要任何领域知识或参数设置,适合于探测性的知识发现。
下图中的伪代码将给出C4.5的基本工作流程:
3.2 算法原理
根据ID3算法的原理可以知道,我们仍然要选取最优划分属性,只是对于C4.5算法而言,属性划分的准则由信息增益变为了信息增益率。为此,我们需要引入信息增益率的概念。
信息增益率:
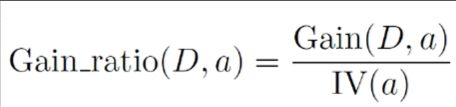
其中:
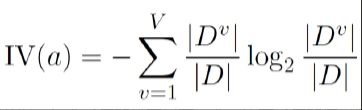
属性 a 的可能取值数目越多 (即 V 越大),则 IV(a) 的值(属性固有值)通常就越大。
每一个样本的编号是不同的,这时按照编号属性进行划分时,每个子集的样本只有一个,所有子集的信息熵为0,则划分后的信息熵0,该属性的信息增益是最大的,但这种划分不具备泛化能力,为了减少这种不利影响,著名的决策树算法C4.5不知用信息增益,而是用增益率。
增益率对于可能取值数目较少的属性有所偏好,因此C4.5不直接采用信息率最大的属性作为候选划分属性,而是使用一个启发式:所谓启发式:就是先从候选划分属性中找出信息增益高于平均水平的,再从中选取增益率最高的。
3.3 算法实例
其中,信息熵的计算、数据集的划分及叶子结点处理过程同ID3算法
3.3.1 计算信息增益率以选择最好特征
def C45_chooseBestFeatureToSplit(dataset):
numFeatures = len(dataset[0]) - 1
baseEnt = cal_entropy(dataset)
bestInfoGain_ratio = 0.0
bestFeature = -1
for i in range(numFeatures): # 遍历所有特征
featList = [example[i] for example in dataset]
uniqueVals = set(featList) # 将特征列表创建成为set集合,元素不可重复。创建唯一的分类标签列表
newEnt = 0.0
IV = 0.0
for value in uniqueVals: # 计算每种划分方式的信息熵
subdataset = splitdataset(dataset, i, value)
p = len(subdataset) / float(len(dataset))
newEnt += p * cal_entropy(subdataset)
IV = IV - p * log(p, 2)
infoGain = baseEnt - newEnt
if (IV == 0): # fix the overflow bug
continue
infoGain_ratio = infoGain / IV # 这个feature的infoGain_ratio
print(u"C4.5中第%d个特征的信息增益率为:%.3f" % (i, infoGain_ratio))
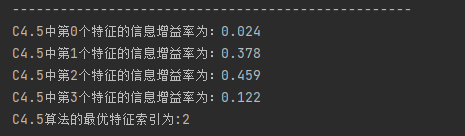
if (infoGain_ratio > bestInfoGain_ratio): # 选择最大的gain ratio
bestInfoGain_ratio = infoGain_ratio
bestFeature = i # 选择最大的gain ratio对应的feature
return bestFeature
3.3.2 建立决策树
def C45_createTree(dataset, labels, test_dataset):
classList = [example[-1] for example in dataset]
if classList.count(classList[0]) == len(classList):
# 类别完全相同,停止划分
return classList[0]
if len(dataset[0]) == 1:
# 遍历完所有特征时返回出现次数最多的
return majorityCnt(classList)
bestFeat = C45_chooseBestFeatureToSplit(dataset)
bestFeatLabel = labels[bestFeat]
print(u"此时最优索引为:" + (bestFeatLabel))
C45Tree = {bestFeatLabel: {}}
del (labels[bestFeat])
# 得到列表包括节点所有的属性值
featValues = [example[bestFeat] for example in dataset]
uniqueVals = set(featValues)
if pre_pruning:
ans = []
for index in range(len(test_dataset)):
ans.append(test_dataset[index][-1])
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
root_acc = cal_acc(test_output=[leaf_output] * len(test_dataset), label=ans)
outputs = []
ans = []
for value in uniqueVals:
cut_testset = splitdataset(test_dataset, bestFeat, value)
cut_dataset = splitdataset(dataset, bestFeat, value)
for vec in cut_testset:
ans.append(vec[-1])
result_counter = Counter()
for vec in cut_dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
outputs += [leaf_output] * len(cut_testset)
cut_acc = cal_acc(test_output=outputs, label=ans)
if cut_acc <= root_acc:
return leaf_output
for value in uniqueVals:
subLabels = labels[:]
C45Tree[bestFeatLabel][value] = C45_createTree(
splitdataset(dataset, bestFeat, value),
subLabels,
splitdataset(test_dataset, bestFeat, value))
if post_pruning:
tree_output = classifytest(C45Tree,
featLabels=['年龄段', '有工作', '有自己的房子', '信贷情况'],
testDataSet=test_dataset)
ans = []
for vec in test_dataset:
ans.append(vec[-1])
root_acc = cal_acc(tree_output, ans)
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
cut_acc = cal_acc([leaf_output] * len(test_dataset), ans)
if cut_acc >= root_acc:
return leaf_output
return C45Tree
四、CART算法
4.1 算法流程
分类回归树(classification and regression tree,CART)模型由Breiman等人在1984年提出,是应用广泛的决策树学习方法。CART同样由特征选择、树的生成以及剪枝组成,既可以用于分类也可以用于回归。同样属于决策树的一种。
4.2 算法原理
CART算法采用的是一种二分递归分割的技术,将当前样本分成两个子样本集,使得生成的非叶子节点都有两个分支。因此CART实际上是一颗二叉树。
4.3 基尼指数
在CART算法中,使用基尼指数来选取最优特征划分,基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A=a)表示集合D经A=a分割后的不确定性(类似于熵),基尼指数越小,样本的不确定性越小。
分类问题中,假设有K个类,样本点属于第k类的概率为pk,则概率分布的基尼指数定义为:
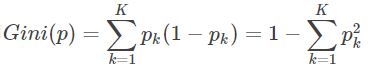
如果样本集合D根据特征A是否取某一可能值aa被分割成D1和D2两部分,即:
4.4 算法实例
4.4.1 计算基尼指数以选择最好特征
def CART_chooseBestFeatureToSplit(dataset):
numFeatures = len(dataset[0]) - 1
bestGini = 999999.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataset]
uniqueVals = set(featList)
gini = 0.0
for value in uniqueVals:
subdataset = splitdataset(dataset, i, value)
p = len(subdataset) / float(len(dataset))
subp = len(splitdataset(subdataset, -1, '0')) / float(len(subdataset))
gini += p * (1.0 - pow(subp, 2) - pow(1 - subp, 2))
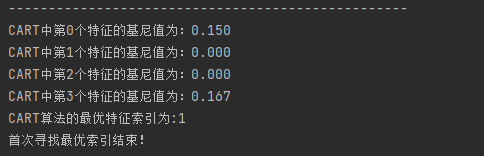
print(u"CART中第%d个特征的基尼值为:%.3f" % (i, gini))
if (gini < bestGini):
bestGini = gini
bestFeature = i
return bestFeature
4.4.2 建立决策树
def CART_createTree(dataset, labels, test_dataset):
classList = [example[-1] for example in dataset]
if classList.count(classList[0]) == len(classList):
# 类别完全相同,停止划分
return classList[0]
if len(dataset[0]) == 1:
# 遍历完所有特征时返回出现次数最多的
return majorityCnt(classList)
bestFeat = CART_chooseBestFeatureToSplit(dataset)
# print(u"此时最优索引为:"+str(bestFeat))
bestFeatLabel = labels[bestFeat]
print(u"此时最优索引为:" + (bestFeatLabel))
CARTTree = {bestFeatLabel: {}}
del (labels[bestFeat])
# 得到列表包括节点所有的属性值
featValues = [example[bestFeat] for example in dataset]
uniqueVals = set(featValues)
if pre_pruning:
ans = []
for index in range(len(test_dataset)):
ans.append(test_dataset[index][-1])
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
root_acc = cal_acc(test_output=[leaf_output] * len(test_dataset), label=ans)
outputs = []
ans = []
for value in uniqueVals:
cut_testset = splitdataset(test_dataset, bestFeat, value)
cut_dataset = splitdataset(dataset, bestFeat, value)
for vec in cut_testset:
ans.append(vec[-1])
result_counter = Counter()
for vec in cut_dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
outputs += [leaf_output] * len(cut_testset)
cut_acc = cal_acc(test_output=outputs, label=ans)
if cut_acc <= root_acc:
return leaf_output
for value in uniqueVals:
subLabels = labels[:]
CARTTree[bestFeatLabel][value] = CART_createTree(
splitdataset(dataset, bestFeat, value),
subLabels,
splitdataset(test_dataset, bestFeat, value))
if post_pruning:
tree_output = classifytest(CARTTree,
featLabels=['年龄段', '有工作', '有自己的房子', '信贷情况'],
testDataSet=test_dataset)
ans = []
for vec in test_dataset:
ans.append(vec[-1])
root_acc = cal_acc(tree_output, ans)
result_counter = Counter()
for vec in dataset:
result_counter[vec[-1]] += 1
leaf_output = result_counter.most_common(1)[0][0]
cut_acc = cal_acc([leaf_output] * len(test_dataset), ans)
if cut_acc >= root_acc:
return leaf_output
return CARTTree
五、决策树剪枝
5.1 算法目的
在决策树、ID3、C4.5算法一文中,简单地介绍了决策树模型,以及决策树生成算法:决策树生成算法递归地产生决策树,直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确,但对未知的测试数据的分类却没有那么准确,即容易出现过拟合现象。解决这个问题的办法是考虑决策树的复杂度,对已生成的决策树进行简化,下面来探讨以下决策树剪枝算法。
决策树的剪枝是为了简化决策树模型,避免过拟合。
- 同样层数的决策树,叶结点的个数越多就越复杂;同样的叶结点个数的决策树,层数越多越复杂。
- 剪枝前相比于剪枝后,叶结点个数和层数只能更多或者其中一特征一样多,剪枝前必然更复杂。
- 层数越多,叶结点越多,分的越细致,对训练数据分的也越深,越容易过拟合,导致对测试数据预测时反而效果差,泛化能力差。
5.2 算法思路
剪去决策树模型中的一些子树或者叶结点,并将其上层的根结点作为新的叶结点,从而减少了叶结点甚至减少了层数,降低了决策树复杂度。决策树的剪枝往往通过极小化决策树整体的损失函数或代价函数来实现。
5.3 剪枝类型
决策树的剪枝基本策略有预剪枝 (Pre-Pruning) 和 后剪枝 (Post-Pruning) ]。根据周志华老师《机器学习》一书中所描述是先对数据集划分成训练集和验证集,训练集用来决定树生成过程中每个结点划分所选择的属性;验证集在预剪枝中用于决定该结点是否有必要依据该属性进行展开,在后剪枝中用于判断该结点是否需要进行剪枝。
5.3.1 预剪枝
预剪枝是在决策树生成过程中,对树进行剪枝,提前结束树的分支生长。加入预剪枝后的决策树生成流程图如下:
#计算数据集的基尼指数
def calcGini(dataSet):
numEntries=len(dataSet)
labelCounts={}
#给所有可能分类创建字典
for featVec in dataSet:
currentLabel=featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1
Gini=1.0
#以2为底数计算香农熵
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
Gini-=prob*prob
return Gini
#对离散变量划分数据集,取出该特征取值为value的所有样本
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#对连续变量划分数据集,direction规定划分的方向,
#决定是划分出小于value的数据样本还是大于value的数据样本集
def splitContinuousDataSet(dataSet,axis,value,direction):
retDataSet=[]
for featVec in dataSet:
if direction==0:
if featVec[axis]>value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
else:
if featVec[axis]<=value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet,labels):
numFeatures=len(dataSet[0])-1
bestGiniIndex=100000.0
bestFeature=-1
bestSplitDict={}
for i in range(numFeatures):
featList=[example[i] for example in dataSet]
#对连续型特征进行处理
if type(featList[0]).__name__=='float' or type(featList[0]).__name__=='int':
#产生n-1个候选划分点
sortfeatList=sorted(featList)
splitList=[]
for j in range(len(sortfeatList)-1):
splitList.append((sortfeatList[j]+sortfeatList[j+1])/2.0)
bestSplitGini=10000
slen=len(splitList)
#求用第j个候选划分点划分时,得到的信息熵,并记录最佳划分点
for j in range(slen):
value=splitList[j]
newGiniIndex=0.0
subDataSet0=splitContinuousDataSet(dataSet,i,value,0)
subDataSet1=splitContinuousDataSet(dataSet,i,value,1)
prob0=len(subDataSet0)/float(len(dataSet))
newGiniIndex+=prob0*calcGini(subDataSet0)
prob1=len(subDataSet1)/float(len(dataSet))
newGiniIndex+=prob1*calcGini(subDataSet1)
if newGiniIndex<bestSplitGini:
bestSplitGini=newGiniIndex
bestSplit=j
#用字典记录当前特征的最佳划分点
bestSplitDict[labels[i]]=splitList[bestSplit]
GiniIndex=bestSplitGini
#对离散型特征进行处理
else:
uniqueVals=set(featList)
newGiniIndex=0.0
#计算该特征下每种划分的信息熵
for value in uniqueVals:
subDataSet=splitDataSet(dataSet,i,value)
prob=len(subDataSet)/float(len(dataSet))
newGiniIndex+=prob*calcGini(subDataSet)
GiniIndex=newGiniIndex
if GiniIndex<bestGiniIndex:
bestGiniIndex=GiniIndex
bestFeature=i
#若当前节点的最佳划分特征为连续特征,则将其以之前记录的划分点为界进行二值化处理
#即是否小于等于bestSplitValue
#并将特征名改为 name<=value的格式
if type(dataSet[0][bestFeature]).__name__=='float' or type(dataSet[0][bestFeature]).__name__=='int':
bestSplitValue=bestSplitDict[labels[bestFeature]]
labels[bestFeature]=labels[bestFeature]+'<='+str(bestSplitValue)
for i in range(shape(dataSet)[0]):
if dataSet[i][bestFeature]<=bestSplitValue:
dataSet[i][bestFeature]=1
else:
dataSet[i][bestFeature]=0
return bestFeature
#特征若已经划分完,节点下的样本还没有统一取值,则需要进行投票
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
return max(classCount)
#由于在Tree中,连续值特征的名称以及改为了 feature<=value的形式
#因此对于这类特征,需要利用正则表达式进行分割,获得特征名以及分割阈值
def classify(inputTree,featLabels,testVec):
firstStr=inputTree.keys()[0]
if '<=' in firstStr:
featvalue=float(re.compile("(<=.+)").search(firstStr).group()[2:])
featkey=re.compile("(.+<=)").search(firstStr).group()[:-2]
secondDict=inputTree[firstStr]
featIndex=featLabels.index(featkey)
if testVec[featIndex]<=featvalue:
judge=1
else:
judge=0
for key in secondDict.keys():
if judge==int(key):
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
else:
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
return classLabel
其中的核心思想就是,在每一次实际对结点进行进一步划分之前,先采用验证集的数据来验证划分是否能提高划分的准确性。如果不能,就把结点标记为叶结点并退出进一步划分;如果可以就继续递归生成节点。
5.3.2 后剪枝
后剪枝是在决策树生长完成之后,对树进行剪枝,得到简化版的决策树。对于后剪枝,周志华老师《机器学习》中述说如下:
后剪枝则是先从训练集生成一颗完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来泛化性能提升,则将该子树替换为叶结点。
后剪枝决策树先生成一棵完整的决策树,再从底往顶进行剪枝处理。在以下代码中,使用的是深度优先搜索。
def postPruningTree(inputTree,dataSet,data_test,labels):
firstStr=inputTree.keys()[0]
secondDict=inputTree[firstStr]
classList=[example[-1] for example in dataSet]
featkey=copy.deepcopy(firstStr)
if '<=' in firstStr:
featkey=re.compile("(.+<=)").search(firstStr).group()[:-2]
featvalue=float(re.compile("(<=.+)").search(firstStr).group()[2:])
labelIndex=labels.index(featkey)
temp_labels=copy.deepcopy(labels)
del(labels[labelIndex])
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
if type(dataSet[0][labelIndex]).__name__=='str':
inputTree[firstStr][key]=postPruningTree(secondDict[key],\
splitDataSet(dataSet,labelIndex,key),splitDataSet(data_test,labelIndex,key),copy.deepcopy(labels))
else:
inputTree[firstStr][key]=postPruningTree(secondDict[key],\
splitContinuousDataSet(dataSet,labelIndex,featvalue,key),\
splitContinuousDataSet(data_test,labelIndex,featvalue,key),\
copy.deepcopy(labels))
if testing(inputTree,data_test,temp_labels)<=testingMajor(majorityCnt(classList),data_test):
return inputTree
return majorityCnt(classList)
5.3.3 两种剪枝对比
- 后剪枝决策树通常比预剪枝决策树保留了更多的分支;
- 后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树;
- 后剪枝决策树训练时间开销比未剪枝决策树和预剪枝决策树都要大的多。
六、实验结果
6.1 绘制决策树
在使用python绘制决策树的时候,需要使用到matplotlib库,(安装anaconda即可)。
在绘制树的时候,我们需要知道树的叶子节点和树的深度,从而让我们便于计算节点所处的位置:
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
获取树的深度:
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
thisDepth = getTreeDepth(secondDict[key]) + 1
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth
获取树的叶子节点和树的深度之后,进行树的绘制:
#设置画节点用的盒子的样式
decisionNode = dict(boxstyle = "sawtooth",fc="0.8")
leafNode = dict(boxstyle = "round4",fc="0.8")
#设置画箭头的样式 http://matplotlib.org/api/patches_api.html#matplotlib.patches.FancyArrowPatch
arrow_args = dict(arrowstyle="<-")
#绘图相关参数的设置
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
#annotate函数是为绘制图上指定的数据点xy添加一个nodeTxt注释
#nodeTxt是给数据点xy添加一个注释,xy为数据点的开始绘制的坐标,位于节点的中间位置
#xycoords设置指定点xy的坐标类型,xytext为注释的中间点坐标,textcoords设置注释点坐标样式
#bbox设置装注释盒子的样式,arrowprops设置箭头的样式
'''
figure points:表示坐标原点在图的左下角的数据点
figure pixels:表示坐标原点在图的左下角的像素点
figure fraction:此时取值是小数,范围是([0,1],[0,1]),在图的左下角时xy是(0,0),最右上角是(1,1)
其他位置是按相对图的宽高的比例取最小值
axes points : 表示坐标原点在图中坐标的左下角的数据点
axes pixels : 表示坐标原点在图中坐标的左下角的像素点
axes fraction : 与figure fraction类似,只不过相对于图的位置改成是相对于坐标轴的位置
'''
createPlot.ax1.annotate(nodeTxt,xy=parentPt,\
xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',\
va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
#绘制线中间的文字(0和1)的绘制
def plotMidText(cntrPt,parentPt,txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] #计算文字的x坐标
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] #计算文字的y坐标
createPlot.ax1.text(xMid,yMid,txtString)
#绘制树
def plotTree(myTree,parentPt,nodeTxt):
#获取树的叶子节点
numLeafs = getNumLeafs(myTree)
#获取树的深度
depth = getTreeDepth(myTree)
#firstStr = myTree.keys()[0]
#获取第一个键名
firstStr = list(myTree.keys())[0]
#计算子节点的坐标
cntrPt = (plotTree.xoff + (1.0 + float(numLeafs))/2.0/plotTree.totalW,\
plotTree.yoff)
#绘制线上的文字
plotMidText(cntrPt,parentPt,nodeTxt)
#绘制节点
plotNode(firstStr,cntrPt,parentPt,decisionNode)
#获取第一个键值
secondDict = myTree[firstStr]
#计算节点y方向上的偏移量,根据树的深度
plotTree.yoff = plotTree.yoff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
#递归绘制树
plotTree(secondDict[key],cntrPt,str(key))
else:
#更新x的偏移量,每个叶子结点x轴方向上的距离为 1/plotTree.totalW
plotTree.xoff = plotTree.xoff + 1.0 / plotTree.totalW
#绘制非叶子节点
plotNode(secondDict[key],(plotTree.xoff,plotTree.yoff),\
cntrPt,leafNode)
#绘制箭头上的标志
plotMidText((plotTree.xoff,plotTree.yoff),cntrPt,str(key))
plotTree.yoff = plotTree.yoff + 1.0 / plotTree.totalD
#绘制决策树,inTree的格式为{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
def createPlot(inTree):
#新建一个figure设置背景颜色为白色
fig = plt.figure(1,facecolor='white')
#清除figure
fig.clf()
axprops = dict(xticks=[],yticks=[])
#创建一个1行1列1个figure,并把网格里面的第一个figure的Axes实例返回给ax1作为函数createPlot()
#的属性,这个属性ax1相当于一个全局变量,可以给plotNode函数使用
createPlot.ax1 = plt.subplot(111,frameon=False,**axprops)
#获取树的叶子节点
plotTree.totalW = float(getNumLeafs(inTree))
#获取树的深度
plotTree.totalD = float(getTreeDepth(inTree))
#节点的x轴的偏移量为-1/plotTree.totlaW/2,1为x轴的长度,除以2保证每一个节点的x轴之间的距离为1/plotTree.totlaW*2
plotTree.xoff = -0.5/plotTree.totalW
plotTree.yoff = 1.0
plotTree(inTree,(0.5,1.0),'')
plt.show()
6.2 main.py
将数据集跑在决策树上:
def classifytest(inputTree, featLabels, testDataSet):
"""
输入:决策树,分类标签,测试数据集
输出:决策结果
描述:跑决策树
"""
classLabelAll = []
for testVec in testDataSet:
classLabelAll.append(classify(inputTree, featLabels, testVec))
return classLabelAll
主函数:
if __name__ == '__main__':
filename = 'dataset.txt'
testfile = 'testset.txt'
dataset, labels = read_dataset(filename)
# dataset,features=createDataSet()
print('dataset', dataset)
print("---------------------------------------------")
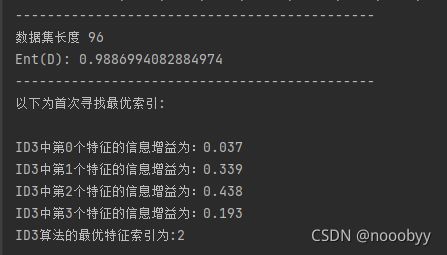
print(u"数据集长度", len(dataset))
print("Ent(D):", cal_entropy(dataset))
print("---------------------------------------------")
print(u"以下为首次寻找最优索引:\n")
print(u"ID3算法的最优特征索引为:" + str(ID3_chooseBestFeatureToSplit(dataset)))
print("--------------------------------------------------")
print(u"C4.5算法的最优特征索引为:" + str(C45_chooseBestFeatureToSplit(dataset)))
print("--------------------------------------------------")
print(u"CART算法的最优特征索引为:" + str(CART_chooseBestFeatureToSplit(dataset)))
print(u"首次寻找最优索引结束!")
print("---------------------------------------------")
print(u"下面开始创建相应的决策树-------")
while True:
dec_tree = '1'
# ID3决策树
if dec_tree == '1':
labels_tmp = labels[:] # 拷贝,createTree会改变labels
ID3desicionTree = ID3_createTree(dataset, labels_tmp, test_dataset=read_testset(testfile))
print('ID3desicionTree:\n', ID3desicionTree)
# treePlotter.createPlot(ID3desicionTree)
treePlotter.ID3_Tree(ID3desicionTree)
testSet = read_testset(testfile)
print("下面为测试数据集结果:")
print('ID3_TestSet_classifyResult:\n', classifytest(ID3desicionTree, labels, testSet))
print("---------------------------------------------")
# C4.5决策树
if dec_tree == '2':
labels_tmp = labels[:] # 拷贝,createTree会改变labels
C45desicionTree = C45_createTree(dataset, labels_tmp, test_dataset=read_testset(testfile))
print('C45desicionTree:\n', C45desicionTree)
treePlotter.C45_Tree(C45desicionTree)
testSet = read_testset(testfile)
print("下面为测试数据集结果:")
print('C4.5_TestSet_classifyResult:\n', classifytest(C45desicionTree, labels, testSet))
print("---------------------------------------------")
# CART决策树
if dec_tree == '3':
labels_tmp = labels[:] # 拷贝,createTree会改变labels
CARTdesicionTree = CART_createTree(dataset, labels_tmp, test_dataset=read_testset(testfile))
print('CARTdesicionTree:\n', CARTdesicionTree)
treePlotter.CART_Tree(CARTdesicionTree)
testSet = read_testset(testfile)
print("下面为测试数据集结果:")
print('CART_TestSet_classifyResult:\n', classifytest(CARTdesicionTree, labels, testSet))
break
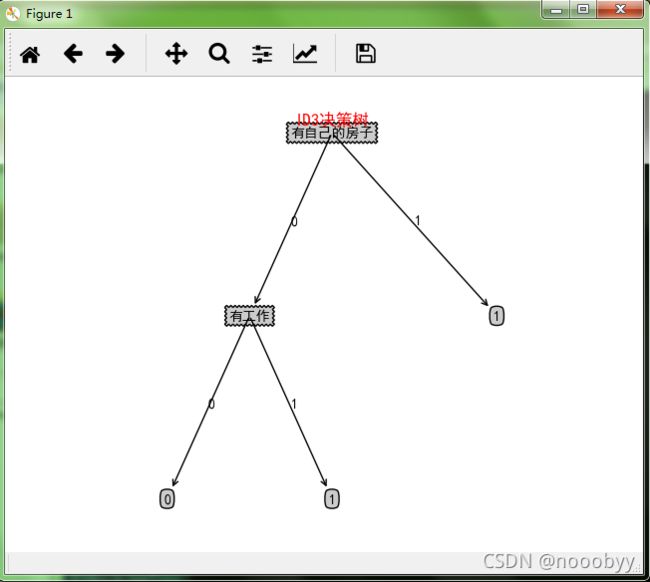
6.3 ID3决策树
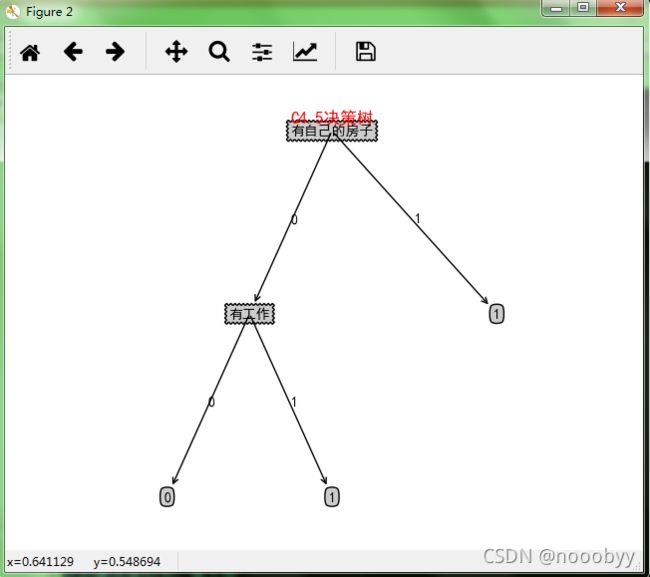
6.4 C4.5决策树
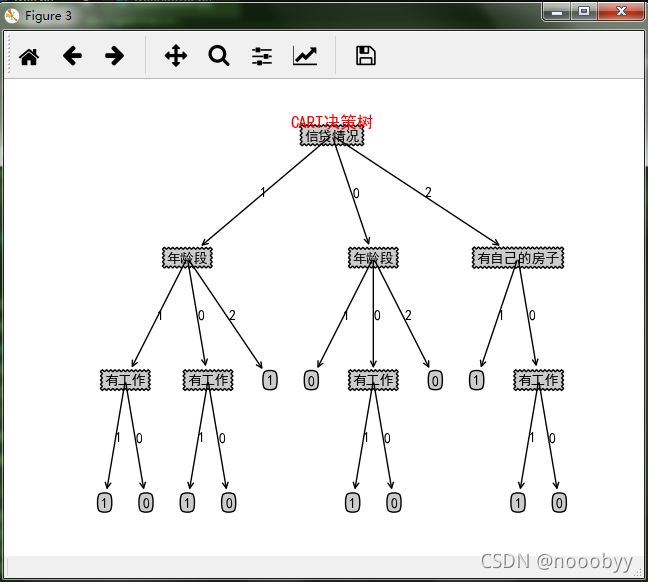
6.5 CART决策树
七、实验总结
- 通过本次实验,可以得到一个建立决策树的基本思想——实际上就是寻找最纯净的划分方法,这个最纯净在数学上叫纯度,纯度通俗点理解就是目标变量要分得足够开。另一种理解是分类误差率的一种衡量。实际决策树算法往往用到的是,纯度的另一面也即不纯度,而不纯度的选取有多种方法,每种方法也就形成了不同的决策树方法,ID3算法使用信息增益作为不纯度;C4.5算法使用信息增益率作为不纯度;CART算法使用基尼系数作为不纯度。
- 学会对决策树采取优化策略——剪枝。剪枝的目的实际是为了避免决策树模型的过拟合。因为决策树算法在学习的过程中为了尽可能的正确的分类训练样本,不停地对结点进行划分,因此这会导致整棵树的分支过多,也就导致了过拟合。
通过实验中对决策树进行剪枝的过程,能够发现,后剪枝决策树通常比预剪枝决策树保留了更多的分支,一般情形下,后剪枝决策树的欠拟合风险小,泛华性能往往也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的,并且要自底向上的对树中的所有非叶结点进行逐一考察,因此其训练时间开销要比未剪枝决策树和预剪枝决策树都大得多。 - 关于决策树的绘制——可视化决策树。 在建立好决策树之后,我们使用Matplotlib模块来绘制决策树,Matplotlib提供了一个注解工具:annotations,可以在数据图形上添加文本工具。它实际上是一套面向对象的绘图库,它所绘制的图表中的每个绘图元素,例如线条Line2D、文字Text、刻度等在内存中都有一个对象与之对应。
如何放置所有的树节点是关键,首先需要知道的是决策树有多少个叶节点,以便确定x轴的长度,其次还要确定树有多少层,以便确定y轴的高度。