【李航统计学习笔记】第五章:决策树
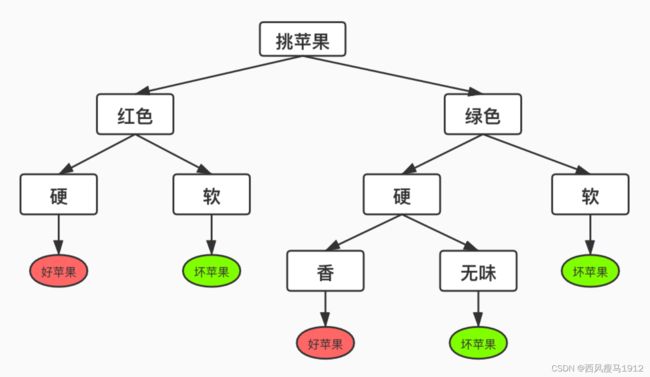
5.1 树的定义
- 树的最顶端叫根节点,所有样本的预测都是从根节点开始的
- 每一个圆形节点表示判断,每个节点只对样本的某个属性进行判断。
- 矩形节点是标记节点,走到矩形节点表示判断结束,将矩形节点中的标签作为对应的预测结果。
怎么构建决策树?
如果苹果的样本还有一个特征叫形状,我们为 形状建立球形和立方型两个分支,显然所有的 样本都会到球形分支里面去,这样的判断没有 进行有效地划分。
此外根据某个特征X,10个苹果中9个会进入A 分支,1个进入B分支。而根据另一个特征Y,5 个进入A分支,5个进入B分支,显然特征Y要好。
决策树模型怎么玩?
- 目前来看,决策树的预测阶段,每进来一个样本,根据判断节点实际情况,对对应的特征 进行判断,直到走到标记节点。
- 如何构建决策树。
A. 按顺序对每一个特征进行判断 (低效)
B. 每个判断节点都尽可能让一半进入A分支, 另一半进入B分支。(高效)
信息熵
-
每走一步,我们都在确定苹果的好坏
-
在根节点时,我们对苹果的好坏一无所知。
-
进过对颜色的判断后,如果是红色,我们明 白好坏的概率是1/2。虽然还包含了1/2的不确 定性。
-
如果苹果红色的前提下又硬,我们100%确 定它是好苹果。此时不确定性坍塌为0。
-
这是一个减少不确定性的过程
什么是信息的不确定性?
在信息论语概率统计中,熵(entropy)是表示随机变量不确定性的度量,设X是一个取有限个值的离散随机变量,其概率分布为
P ( X = x i ) = p i , i = 1 , 2 , … , n P\left(X=x_{i}\right)=p_{i}, \quad i=1,2, \ldots, n P(X=xi)=pi,i=1,2,…,n
则随机变量X的熵定义为
H ( X ) = − ∑ i = 1 n p i log p i H(X)=-\sum_{i=1}^{n} p_{i} \log p_{i} H(X)=−i=1∑npilogpi
熵越大,则随机变量的不确定性越大。其中 0 ≤ H ( P ) ≤ log n 0 \leq H(P) \leq \log n 0≤H(P)≤logn。( H ( X ) ≤ − ∑ i = 1 n 1 n log 1 n = log n H(X)\le -\sum_{i=1}^{n}\dfrac{1}{n}\log \dfrac{1}{n} = \log n H(X)≤−∑i=1nn1logn1=logn)
假设我们有10个苹果,1个好苹果 A , 9 A , 9 A,9 个坏苹果B。熵的计算如下:
H ( P ) = − ∑ i = 1 n p i log p i = − [ P ( A ) log P ( A ) + P ( B ) log P ( B ) ] = − [ 1 10 log 1 10 + 9 10 log 9 10 ] = 0.47 \begin{aligned} &H(P)=-\sum_{i=1}^{n} p_{i} \log p_{i}=-[P(A) \log P(A)+P(B) \log P(B)] \\ &=-\left[\frac{1}{10} \log \frac{1}{10}+\frac{9}{10} \log \frac{9}{10}\right]=0.47 \end{aligned} H(P)=−i=1∑npilogpi=−[P(A)logP(A)+P(B)logP(B)]=−[101log101+109log109]=0.47
如果有5个好苹果和5个坏苹果呢?
H ( P ) = − ∑ i = 1 n p i log p i = − [ P ( A ) log P ( A ) + P ( B ) log P ( B ) ] = − [ 5 10 log 5 10 + 5 10 log 5 10 ] = 1 \begin{aligned} &H(P)=-\sum_{i=1}^{n} p_{i} \log p_{i}=-[P(A) \log P(A)+P(B) \log P(B)] \\ &=-\left[\frac{5}{10} \log \frac{5}{10}+\frac{5}{10} \log \frac{5}{10}\right]=1 \end{aligned} H(P)=−i=1∑npilogpi=−[P(A)logP(A)+P(B)logP(B)]=−[105log105+105log105]=1
1个坏苹果9个好苹果时,我们可以认为大部分都是坏苹果。内部并不混乱,确定性很大,熵就小。5个坏苹果5个好苹果时,里面就有点乱了,我们并不太能确定随机的一个苹果是好苹果还是坏苹果,熵就大。
在根节点的最初,我们先假设信息樀为 1, 表示我们对于这个苹果一无所知。到叶节点时假设信息熵为 0 ,表示我们非常确定。我们希望尽可能少的次数就能判断出苹果的好坏。也就是希望每个判断节点都能让信息熵下降地快一点。怎么度量下降得快不快呢? 我们需要使用信息增益。
信息增益
信息增益:表示得知特征X的信息而使得类Y的信息的不确定性减少的程度
特征A对认练集D的信息增益 g ( D , A ) g(D, A) g(D,A) ,定义为集合D的经验熵 H ( D ) H(D) H(D)与特征A给定条件下D的经 验条件熵 H ( D ∣ A ) H(D \mid A) H(D∣A) 之差,即
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D, A)=H(D)-H(D \mid A) g(D,A)=H(D)−H(D∣A)
信息增益算法
输入:训练数据集 D D D和特征 A A A
输出:特征 A A A对训练数据集 D D D的信息增益 g ( D , A ) g(D, A) g(D,A)
- 计算数据集 D D D的经验熵 H ( D ) H(D) H(D)
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log \frac{\left|C_{k}\right|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log∣D∣∣Ck∣
- 计算特征A对数据集D的经验条件熵 H ( D ∣ A ) H(D \mid A) H(D∣A)
H ( D ∣ A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ log ∣ D i k ∣ ∣ D i ∣ \begin{aligned} &H(D \mid A)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right) \\ &=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \end{aligned} H(D∣A)=−i=1∑n∣D∣∣Di∣H(Di)=−i=1∑n∣D∣∣Di∣k=1∑K∣Di∣∣Dik∣log∣Di∣∣Dik∣
- 计算信息增益
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D, A)=H(D)-H(D \mid A) g(D,A)=H(D)−H(D∣A)
(补充例子)
信息增益比
如果以信息增益为划分依据,存在偏向选择取值较多的特征,信息增益比是对这一问题进行矫正。
信息增益比:特征 A A A 对训练数据集 D D D 的信息增益比 g R ( D , A ) g_{R}(D, A) gR(D,A) 定义为其信息增益 g ( D , A ) g(D, A) g(D,A) 与训练数据集 D D D 的经验熵 H ( D ) H(D) H(D) 之比:
g R ( D , A ) = g ( D , A ) H ( D ) g_{R}(D, A)=\frac{g(D, A)}{H(D)} gR(D,A)=H(D)g(D,A)
(补充ID3算法,C4.5算法)
总结
- 决策树的核心思想:以树结构为基础,每个节点对某特征 进行判断,进入分支,直到到达叶节点。
- 决策树构造的核心思想:让信息熵快速下降,从而达到最少的判断次数获得标签。
- 判断信息熵下降速度的方法:信息增益
- 构建决策树算法:ID3(使用信息增益)、C4.5(使用信息增益比)
- 信息增益会导致节点偏向选取取值较多的特征的问题。
5.2 剪枝
剪枝的目的是在决策树构造结束后,去裁掉部分枝桠以此降低模型复杂度。因为复杂的算法结构往往可能会造成过拟合的现象。
设树 T T T 的叶节点个数为 ∣ T ∣ |T| ∣T∣, t t t 是树 T T T 的叶节点, 该叶节点有 N t N_{t} Nt 个样本点, 其中 k k k类的样本点有 N t k N_{t k} Ntk 个, k = 1 , 2 , ⋯ , K k=1,2, \cdots, K k=1,2,⋯,K. $ H_{t}(T)$ 为叶节点 t t t 上的经验熵, α ≥ 0 \alpha \geq 0 α≥0 为参数, 则决策树学习的损失函数可以定义为:
C α ( T ) = ∑ t = 1 ∣ T ∣ N t H t ( T ) + α ∣ T ∣ H t ( T ) = − ∑ k N t k N t log N t k N t C α ( T ) = C ( T ) + α ∣ T ∣ \begin{gathered} C_{\alpha}(T)=\sum_{t=1}^{|T|} N_{t} H_{t}(T)+\alpha|T| \\ H_{t}(T)=-\sum_{k} \frac{N_{t k}}{N_{t}} \log \frac{N_{t k}}{N_{t}} \\ C_{\alpha}(T)=C(T)+\alpha|T| \end{gathered} Cα(T)=t=1∑∣T∣NtHt(T)+α∣T∣Ht(T)=−k∑NtNtklogNtNtkCα(T)=C(T)+α∣T∣
剪枝算法:
输入: 生成算法产生的整个树 T T T, 参数 α \alpha α;
输出: 修剪后的子树 T α T_{\alpha} Tα 。
(1) 计算每个结点的经验熵。
(2) 递归地从树的叶结点向上回缩。
设一组叶结点回缩到其父结点之前与之后的整体树分别为 T B T_{B} TB 与 T A T_{A} TA, 其对应的 损失函数值分别是 C α ( T B ) C_{\alpha}\left(T_{B}\right) Cα(TB) 与 C α ( T A ) C_{\alpha}\left(T_{A}\right) Cα(TA), 如果
C α ( T A ) ⩽ C α ( T B ) C_{\alpha}\left(T_{A}\right) \leqslant C_{\alpha}\left(T_{B}\right) Cα(TA)⩽Cα(TB)
则进行剪枝, 即将父结点变为新的叶结点。
(3) 返回(2),直至不能继续为止,得到损失函数最小的子树 T α T_{\alpha} Tα