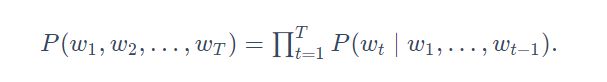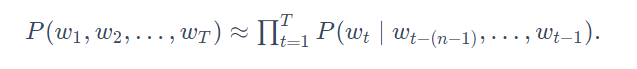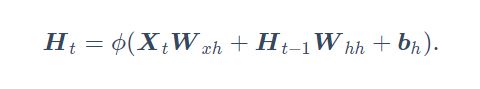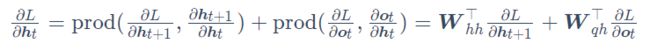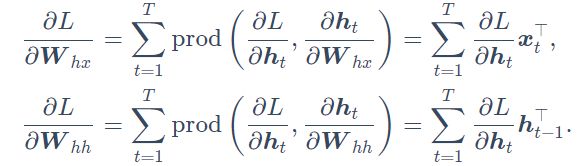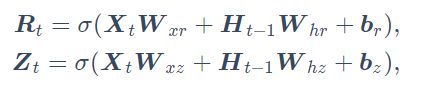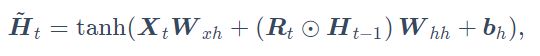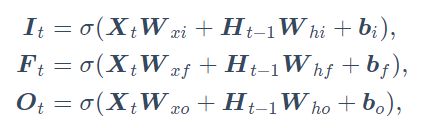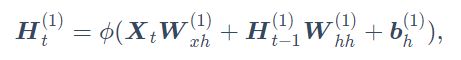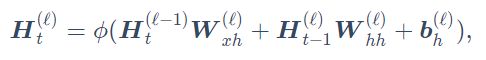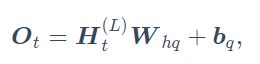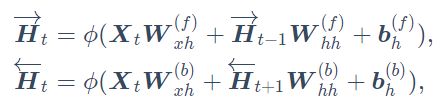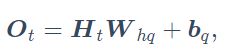动手学深度学习(七、语言模型与循环神经网络)
动手学深度学习(七、语言模型与循环神经网络)
参考链接:循环神经网络
一、语言模型
- 语言模型是自然语言处理的重要技术。
- N元语法是基于n−1阶马尔可夫链的概率语言模型,其中n权衡了计算复杂度和模型准确性。
语言模型(language model)是自然语言处理的重要技术。自然语言处理中最常见的数据是文本数据。我们可以把一段自然语言文本看作一段离散的时间序列。假设一段长度为T的文本中的词依次为![]() ,那么在离散的时间序列中,
,那么在离散的时间序列中,![]() 可看作在时间步(time step)t的输出或标签。语言模型可用于提升语音识别和机器翻译的性能。
可看作在时间步(time step)t的输出或标签。语言模型可用于提升语音识别和机器翻译的性能。
例如:一段含有4个词的文本序列的概率
为了计算语言模型,我们需要计算词的概率,以及一个词在给定前几个词的情况下的条件概率,即语言模型参数。设训练数据集为一个大型文本语料库,如维基百科的所有条目。词的概率可以通过该词在训练数据集中的相对词频来计算。
n元语法
当序列长度增加时,计算和存储多个词共同出现的概率的复杂度会呈指数级增加。N元语法通过马尔可夫假设(虽然并不一定成立)简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面n个词相关,即n阶马尔可夫链(Markov chain of order n)。如果n = 1,那么有P(w3∣w1,w2)=P(w3∣w2)。如果基于n−1阶马尔可夫链,我们可以将语言模型改写为
以上也叫n元语法(n-grams), 它是基于n−1阶马尔可夫链的概率语言模型。当n分别为1、2和3时,我们将其分别称作一元语法(unigram)、二元语法(bigram)和三元语法(trigram).当n较小时,n元语法往往并不准确。例如,在一元语法中,由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而,当n较大时,n元语法需要计算并存储大量的词频和多词相邻频率。
二、循环神经网络
- 使用循环计算的网络即循环神经网络。
- 循环神经网络的隐藏状态可以捕捉截至当前时间步的序列的历史信息。
- 循环神经网络模型参数的数量不随时间步的增加而增长。
- 可以基于字符级循环神经网络来创建语言模型。
它并非刚性地记忆所有固定长度的序列,而是通过隐藏状态来存储之前时间步的信息。
含隐藏状态的循环神经网络
具体来说,时间步t的隐藏变量的计算由当前时间步的输入和上一时间步的隐藏变量共同决定:![]() 是序列中时间步t的小批量输入,
是序列中时间步t的小批量输入, ![]() 是该时间步的隐藏变量, 保存的上一时间步的隐藏变量为
是该时间步的隐藏变量, 保存的上一时间步的隐藏变量为![]() , 并且引入引得权重参数
, 并且引入引得权重参数![]() , 隐藏变量计算如下:
, 隐藏变量计算如下:
这里的隐藏变量能够捕捉截至当前时间步的序列的历史信息,就像是神经网络当前时间步的状态或记忆一样。因此,该隐藏变量也称为隐藏状态。由于隐藏状态在当前时间步的定义使用了上一时间步的隐藏状态,上式的计算是循环的。使用循环计算的网络即循环神经网络(recurrent neural network)。循环神经网络有很多种不同的构造方法。含上式所定义的隐藏状态的循环神经网络是极为常见的一种。在循环神经网络中, 包含n隐藏层的权重![]() , 偏差
, 偏差![]() , 输出层的权重
, 输出层的权重![]() , 以及偏差
, 以及偏差![]() 。即便在不同时间步,循环神经网络也始终使用这些模型参数。因此,循环神经网络模型参数的数量不随时间步的增加而增长。
。即便在不同时间步,循环神经网络也始终使用这些模型参数。因此,循环神经网络模型参数的数量不随时间步的增加而增长。
![]()
import torch
X, W_xh = torch.randn(3, 1), torch.randn(1, 4)
H, W_hh = torch.randn(3, 4), torch.randn(4, 4)
ans1 = torch.matmul(X, W_xh) + torch.matmul(H, W_hh)
mat1 = torch.cat((X, H), dim = 1)
mat2 = torch.cat((W_xh, W_hh), dim = 0)
ans2 = torch.matmul(mat1, mat2)
print(ans1)
print(ans2)
#输出:
tensor([[-1.7134, -0.6014, 1.3412, -1.0023],
[ 1.0881, 2.6679, -2.2030, -0.8946],
[ 0.7392, 2.9640, -2.0951, 1.6413]])
tensor([[-1.7134, -0.6014, 1.3412, -1.0023],
[ 1.0881, 2.6679, -2.2030, -0.8946],
[ 0.7392, 2.9640, -2.0951, 1.6413]])基于字符级循环神经网络的语言模型
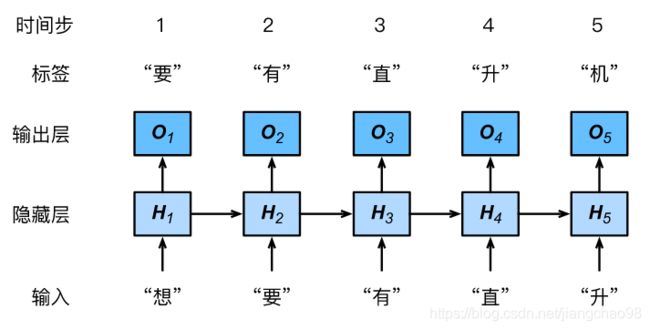
我们介绍如何应用循环神经网络来构建一个语言模型。设小批量中样本数为1,文本序列为“想”“要”“有”“直”“升”“机”。在训练时,我们对每个时间步的输出层输出使用softmax运算,然后使用交叉熵损失函数来计算它与标签的误差。由于隐藏层中隐藏状态的循环计算,时间步3的输出![]() 取决于文本序列“想”“要”“有”。 由于训练数据中该序列的下一个词为“直”,时间步3的损失将取决于该时间步基于序列“想”“要”“有”生成下一个词的概率分布与该时间步的标签“直”。
取决于文本序列“想”“要”“有”。 由于训练数据中该序列的下一个词为“直”,时间步3的损失将取决于该时间步基于序列“想”“要”“有”生成下一个词的概率分布与该时间步的标签“直”。
因为每个输入词是一个字符,因此这个模型被称为字符级循环神经网络(character-level recurrent neural network)。因为不同字符的个数远小于不同词的个数(对于英文尤其如此),所以字符级循环神经网络的计算通常更加简单。
三、语言模型数据集
- 时序数据采样方式包括随机采样和相邻采样。使用这两种方式的循环神经网络训练在实现上略有不同。
将介绍如何预处理一个语言模型数据集,并将其转换成字符级循环神经网络所需要的输入格式。为此,我们收集了周杰伦从第一张专辑《Jay》到第十张专辑《跨时代》中的歌词,并在后面几节里应用循环神经网络来训练一个语言模型。当模型训练好后,我们就可以用这个模型来创作歌词。
读取数据集、建立字符索引
时序数据的采样
在训练中我们需要每次随机读取小批量样本和标签。与之前章节的实验数据不同的是,时序数据的一个样本通常包含连续的字符。假设时间步数为5,样本序列为5个字符,即“想”“要”“有”“直”“升”。该样本的标签序列为这些字符分别在训练集中的下一个字符,即“要”“有”“直”“升”“机”。我们有两种方式对时序数据进行采样,分别是随机采样和相邻采样。
随机采样
下面的代码每次从数据里随机采样一个小批量。其中批量大小batch_size指每个小批量的样本数,num_steps为每个样本所包含的时间步数。在随机采样中,每个样本是原始序列上任意截取的一段序列。相邻的两个随机小批量在原始序列上的位置不一定相毗邻。因此,我们无法用一个小批量最终时间步的隐藏状态来初始化下一个小批量的隐藏状态。在训练模型时,每次随机采样前都需要重新初始化隐藏状态。
相邻采样
除对原始序列做随机采样之外,我们还可以令相邻的两个随机小批量在原始序列上的位置相毗邻。这时候,我们就可以用一个小批量最终时间步的隐藏状态来初始化下一个小批量的隐藏状态,从而使下一个小批量的输出也取决于当前小批量的输入,并如此循环下去。这对实现循环神经网络造成了两方面影响:一方面, 在训练模型时,我们只需在每一个迭代周期开始时初始化隐藏状态;另一方面,当多个相邻小批量通过传递隐藏状态串联起来时,模型参数的梯度计算将依赖所有串联起来的小批量序列。同一迭代周期中,随着迭代次数的增加,梯度的计算开销会越来越大。 为了使模型参数的梯度计算只依赖一次迭代读取的小批量序列,我们可以在每次读取小批量前将隐藏状态从计算图中分离出来。
import torch
import random
import zipfile
with zipfile.ZipFile('./Dive-into-DL-PyTorch-master/data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
#打印前40个字符
print(corpus_chars[:40])
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
#建立字符索引
#set()函数创建一个无序不重复元素集,可进行关系测试,删除重复数据,还可以计算交集、差集、并集等。
idx_to_char = list(set(corpus_chars))
#print(len(idx_to_char))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])#建立索引字典
vocab_size = len(char_to_idx)
print(vocab_size)
print(char_to_idx['想'])
count_ = 0
for i in char_to_idx:
print(i)
count_ = count_ + 1
if count_ >= 5:
break
print("*" * 30 )
corpus_indices = [char_to_idx[char] for char in corpus_chars]
sample = corpus_indices[:20]
print('chars:', ''.join([idx_to_char[idx] for idx in sample]))
print('indices:', sample)
#封装在d2lzh_pytorch 包里的 load_data_jay_lyrics 函数中, 调用函数一次获得 corpus_indices, char_to_idx, idx_to_char, vocab_size 四个变量
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def data_iter_random(corpus_indices, batch_size, num_steps, device = None):
# 减1是因为输出的索引x是相应输入的索引y加1, 因为要使用y 去预测 x
num_examples = (len(corpus_indices) - 1) // num_steps#训练集训练完一次需要训练多少次
epoch_size = num_examples // batch_size
example_indices = list(range(num_examples))
random.shuffle(example_indices)
# 返回从pos开始的长为num_steps的序列
def _data(pos):
return corpus_indices[pos: pos + num_steps]
if device is None:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
for i in range(epoch_size):
# 每次读取batch_size个随机样本
i = i * batch_size
batch_indices = example_indices[i: i+ batch_size]
X = [_data(j * num_steps) for j in batch_indices]
Y = [_data(j * num_steps + 1) for j in batch_indices]
#Python中yield使用方法,yield生成器在遍历时候逐个返回, 遍历的过程就是调用next()的过程,好处就在于使用时候才产生数据,消耗内存。
yield torch.tensor(X, dtype = torch.float32, device = device), torch.tensor(Y, dtype = torch.float32, device = device)
my_seq = list(range(30))
for X, Y in data_iter_random(my_seq, batch_size = 2, num_steps = 6):
print('X: ', X, '\nY: ', Y, '\n')
# 本函数已保存在d2lzh_pytorch包中方便以后使用
def data_iter_consecutive(corpus_indices, batch_size, num_steps, device=None):
if device is None:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
corpus_indices = torch.tensor(corpus_indices, dtype=torch.float32, device=device)
data_len = len(corpus_indices)
batch_len = data_len // batch_size
indices = corpus_indices[0: batch_size*batch_len].view(batch_size, batch_len)
epoch_size = (batch_len - 1) // num_steps
for i in range(epoch_size):
i = i * num_steps
X = indices[:, i: i + num_steps]
Y = indices[:, i + 1: i + num_steps + 1]
yield X, Y
for X, Y in data_iter_consecutive(my_seq, batch_size=2, num_steps=6):
print('X: ', X, '\nY:', Y, '\n')
#输出
想要有直升机
想要和你飞到宇宙去
想要和你融化在一起
融化在宇宙里
我每天每天每
1027
846
阻
埋
必
或
柔
******************************
chars: 想要有直升机 想要和你飞到宇宙去 想要和
indices: [846, 677, 475, 178, 157, 403, 350, 846, 677, 599, 960, 373, 567, 229, 746, 225, 350, 846, 677, 599]
X: tensor([[12., 13., 14., 15., 16., 17.],
[ 0., 1., 2., 3., 4., 5.]], device='cuda:0')
Y: tensor([[13., 14., 15., 16., 17., 18.],
[ 1., 2., 3., 4., 5., 6.]], device='cuda:0')
X: tensor([[ 6., 7., 8., 9., 10., 11.],
[18., 19., 20., 21., 22., 23.]], device='cuda:0')
Y: tensor([[ 7., 8., 9., 10., 11., 12.],
[19., 20., 21., 22., 23., 24.]], device='cuda:0')
X: tensor([[ 0., 1., 2., 3., 4., 5.],
[15., 16., 17., 18., 19., 20.]], device='cuda:0')
Y: tensor([[ 1., 2., 3., 4., 5., 6.],
[16., 17., 18., 19., 20., 21.]], device='cuda:0')
X: tensor([[ 6., 7., 8., 9., 10., 11.],
[21., 22., 23., 24., 25., 26.]], device='cuda:0')
Y: tensor([[ 7., 8., 9., 10., 11., 12.],
[22., 23., 24., 25., 26., 27.]], device='cuda:0')
四、循环神经网络从零开始
- 可以用基于字符级循环神经网络的语言模型来生成文本序列,例如创作歌词。
- 当训练循环神经网络时,为了应对梯度爆炸,可以裁剪梯度。
- 困惑度是对交叉熵损失函数做指数运算后得到的值。
在本节中,我们将从零开始实现一个基于字符级循环神经网络的语言模型,并在周杰伦专辑歌词数据集上训练一个模型来进行歌词创作。首先,我们读取周杰伦专辑歌词数据集:
one-hot向量
为了将词表示成向量输入到神经网络,一个简单的办法是使用one-hot向量。假设词典中不同字符的数量为N(即词典大小vocab_size),每个字符已经同一个从0到N−1的连续整数值索引一一对应。如果一个字符的索引是整数iii, 那么我们创建一个全0的长为N的向量,并将其位置为i的元素设成1。该向量就是对原字符的one-hot向量。
我们每次采样的小批量的形状是(批量大小, 时间步数)。下面的函数to_onehot()将这样的小批量变换成数个可以输入进网络的形状为(批量大小, 词典大小)的矩阵, 矩阵个数等于时间步数。
初始化模型参数
隐藏单元个数 num_hiddens是一个超参数。
定义模型
根据循环神经网络的计算表达式实现该模型。首先定义init_rnn_state函数来返回初始化的隐藏状态。它返回由一个形状为(批量大小, 隐藏单元个数)的值为0的NDArray组成的元组。使用元组是为了更便于处理隐藏状态含有多个NDArray的情况。
定义预测模型
以下函数基于前缀prefix(含有数个字符的字符串)来预测接下来的num_chars个字符。
裁剪梯度
循环神经网络中较容易出现梯度衰减或梯度爆炸。为了应对梯度爆炸,我们可以裁剪梯度(clip gradient)。我们把所有模型参数梯度的元素拼接成一个向量 ![]() ,并设裁剪的阈值是
,并设裁剪的阈值是![]() 。裁剪后的梯度
。裁剪后的梯度![]() 的
的![]() 范数不超过
范数不超过![]()
困惑度
我们通常使用困惑度(perplexity)来评价语言模型的好坏。困惑度是对交叉熵损失函数做指数运算后得到的值。特别地,
- 最佳情况下,模型总是把标签类别的概率预测为1,此时困惑度为1;
- 最坏情况下,模型总是把标签类别的概率预测为0,此时困惑度为正无穷;
- 基线情况下,模型总是预测所有类别的概率都相同,此时困惑度为类别个数。
显然,任何一个有效模型的困惑度必须小于类别个数。
定义模型训练函数
这里的模型训练函数有以下几点不同:
- 使用困惑度评价模型。
- 在迭代模型参数前裁剪梯度。
- 对时序数据采用不同采样方法将导致隐藏状态初始化的不同。
另外,考虑到后面将介绍的其他循环神经网络,为了更通用,这里的函数实现更长一些。
#2021-4-15 16:30 6.4
import time
import math
import torch
from torch import nn, optim
import torch.nn.functional as F
import numpy as np
import zipfile
import sys
sys.path.append("F:\数据\MRC\动手学深度学习\Dive-into-DL-PyTorch-master\code")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def load_data_jay_lyrics():
"""加载周杰伦歌词数据集"""
with zipfile.ZipFile('./Dive-into-DL-PyTorch-master/data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
idx_to_char = list(set(corpus_chars))
#char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx)
corpus_indices = [char_to_idx[char] for char in corpus_chars]
return corpus_indices, char_to_idx, idx_to_char, vocab_size
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
# print(len(corpus_indices))#使用前1万个字符来训练模型
# print(len(char_to_idx))#保存字典信息, key为出现的字, value为字典序列编号
# print(type(char_to_idx))
# count_ = 0
# for i in char_to_idx:
# print(i, end = " ")
# print(char_to_idx[i])
# count_ += 1
# if count_ >= 3:
# break
# print(len(idx_to_char))#保存列表信息,保存所有的出现的字
# print(type(idx_to_char))
# for i in range(5):
# print(idx_to_char[i])
# print(vocab_size)#词表的长度为1027
#1、one-hot向量
def one_hot(x, n_class, dtype=torch.float32):
# X shape: (batch), output shape: (batch, n_class)
x = x.long()
res = torch.zeros(x.shape[0], n_class, dtype=dtype, device=x.device)
res.scatter_(1, x.view(-1, 1), 1)
return res
x = torch.tensor([0, 2])
print(one_hot(x, vocab_size))
# 本函数已保存在d2lzh_pytorch包中方便以后使用
# 矩阵个数等于时间步数
def to_onehot(X, n_class):
# X shape: (batch, seq_len), output: seq_len elements of (batch, n_class)
return [one_hot(X[:, i], n_class) for i in range(X.shape[1])]
X = torch.arange(10).view(2, 5)
print(X)
inputs = to_onehot(X, vocab_size)
print(len(inputs))
# for i in range(len(inputs)):
# print(inputs[i])
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
#2、初始化模型参数
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size = shape), device = device, dtype = torch.float32)
return torch.nn.Parameter(ts, requires_grad = True)
#隐藏层参数
W_xh = _one((num_inputs, num_hiddens))
W_hh = _one((num_hiddens, num_hiddens))
b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device = device, requires_grad = True))
#输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device = device, requires_grad = True))
return nn.ParameterList([W_xh, W_hh, b_h, W_hq, b_q])
#3、定义模型
#初始状态矩阵初始化
def init_rnn_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device = device), )
#rnn函数定义了在一个时间步里如何计算隐藏状态和输出, 激活函数使用tanh函数
def rnn(inputs, state, params):
# inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
W_xh, W_hh, b_h, W_hq, b_q = params #模型训练的参数
H, = state #初始隐藏状态
outputs = []
for X in inputs:
H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
state = init_rnn_state(X.shape[0], num_hiddens, device)#初始化隐藏状态
print(state[0].shape)
inputs = to_onehot(X.to(device), vocab_size)#(batch_size, inputs)初始输入
params = get_params()#模型训练参数
outputs, state_new = rnn(inputs, state, params)
#print(len(outputs), outputs[0].shape, state_new[0].shape)
#4、定义预测函数
#以下函数基于前缀prefix来预测接下来的num_chars个字符。将循环神经单元rnn设置成函数参数
def predict_rnn(prefix, num_chars, rnn, params, init_rnn_state, num_hiddens, vocab_size, device, idx_to_char, char_to_idx):
state = init_rnn_state(1, num_hiddens, device)#初始化隐藏状态,batch_size = 1
output = [char_to_idx[prefix[0]]]#字典序列(字:编号), 通过汉字转换为数字id
# print(prefix[0])
# print(char_to_idx[prefix[0]])
# print(output)
# print(output[-1])
# print(torch.tensor([[output[-1]]], device = device))
for t in range(num_chars + len(prefix) - 1):
#将上一时间步的输出作为当前时间步的输入
X = to_onehot(torch.tensor([[output[-1]]], device = device), vocab_size) #生成X为输出数据, 每一次输入X只有一个
#print(X)
#计算输出和更新隐藏状态
(Y, state) = rnn(X, state, params)
# print(len(Y))
# print(Y[0].shape)
# print(Y[0])
# print(Y[0].argmax(dim = 1))
#下一个时间步的输入是prefix里的字符或者当前的最佳预测字符
#output中append下一个预测的数字
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y[0].argmax(dim = 1).item()))
return ''.join([idx_to_char[i] for i in output])
predict_rnn('分开', 10, rnn, params, init_rnn_state, num_hiddens, vocab_size, device, idx_to_char, char_to_idx)
#预测函数根据每一步的输入、给出输出以及状态矩阵, 将给出的输出转换成汉字保存于列表中,打印显示
norm = torch.tensor([0.0], device = device)
print(norm)
#5、裁剪梯度
def grad_clipping(params, theta, device):
norm = torch.tensor([0.0], device = device)
for param in params:
norm += (param.grad.data ** 2).sum()
norm = norm.sqrt().item()#norm为计算的L2范数
if norm > theta:
for param in params:
param.grad.data *= (theta / norm) #减小梯度
print('*' * 100)
#7、定义模型训练函数
#rnn是训练函数, get_params是初始化模型参数的方法, init_rnn_state初始化隐藏状态
def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens, vocab_size, device, corpus_indices, idx_to_char, char_to_idx,
is_random_iter, num_epochs, num_steps, lr, clipping_theta, batch_size, pred_period, pred_len, prefixes):
#使用随机采样还是相邻采样
if is_random_iter:
data_iter_fn = d2l.data_iter_random
else:
data_iter_fn = d2l.data_iter_consecutive
params = get_params()
loss = nn.CrossEntropyLoss()
for epoch in range(num_epochs):
if not is_random_iter: # 如使用相邻采样,在epoch开始时初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
l_sum, n, start = 0.0, 0, time.time()#? #n起到计数的作用
data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
for X, Y in data_iter:
if is_random_iter: #如果使用随机采样, 在每个小批量更新前初始化隐藏状态
state = init_rnn_state(batch_size, num_hiddens, device)
else:
for s in state:
s.detach_()#计算图分离
inputs = to_onehot(X, vocab_size)
(outputs, state) = rnn(inputs, state, params)
outputs = torch.cat(outputs, dim = 0)
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
l = loss(outputs, y.long())#损失函数的由来?
#梯度清零
if params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
grad_clipping(params, clipping_theta, device)#梯度裁剪
d2l.sgd(params, lr, 1)
l_sum += l.item() * y.shape[0]
n += y.shape[0]
#50批次输出
if (epoch + 1) % pred_period == 0:
#困惑度:交叉熵损失函数做指数运算
print('epoch %d, perplexity %f, time %.2f sec' % (epoch + 1, math.exp(l_sum / n), time.time() - start))
for prefix in prefixes:
print('-', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state, num_hiddens, vocab_size, device, idx_to_char, char_to_idx))
#8、训练模型
num_epochs, num_steps, batch_size, lr, clipping_theta = 250, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 50, 50, ['分开', '不分开']
#训练函数、参数初始化函数、隐藏状态初始化函数、隐藏层维度、词表、运算设备、所有训练的字、列表保存字、字典(字->数字id)、是否采用随机采样
#训练的循环次, 训练的时间步、学习率、裁剪梯度的阈值、每批次训练数、每多少步打印一次信息、预测的长度、开始的词
train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens, vocab_size, device, corpus_indices, idx_to_char, char_to_idx, True,
num_epochs, num_steps, lr, clipping_theta, batch_size, pred_period, pred_len, prefixes)输出:
tensor([[1., 0., 0., ..., 0., 0., 0.],
[0., 0., 1., ..., 0., 0., 0.]])
tensor([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
5
will use cuda
torch.Size([2, 256])
tensor([0.], device='cuda:0')
****************************************************************************************************
epoch 50, perplexity 66.987650, time 0.16 sec
- 分开 我想你的可爱 我知你的让我 我有你的让我 我有你的让我 我有你的让我 我有你的让我 我有你的让我
- 不分开 我想你的可写 我知你的让我 我有你的让我 我有你的让我 我有你的让我 我有你的让我 我有你的让我
epoch 100, perplexity 9.857417, time 0.16 sec
- 分开 快使我 别怪我 说你怎么 在人的 快 我 别头四步三在 草 在我胸 我不 我不 我不要再想你 不知
- 不分开你 我不要再想你 不果不觉 你已经离开我 不知不觉 我该好好生奏 我知后好生活的课斑鸠 印着一只饿昏
epoch 150, perplexity 2.909719, time 0.15 sec
- 分开 一只到不一步四侬 就念死午了写欢默a道 我的完会呵你 太彻我 你子你的传快就像龙卷风 不不承受我妈
- 不分开扫 我后你的爱写在西元前 深埋在美索不达米亚平原 几十个文字后出了发现 泥板上的字迹依然清晰 见的完
epoch 200, perplexity 1.587691, time 0.16 sec
- 分开 一只心它子仪的母斑鸠 印仔红蕃 在小镇 背对背决斗 一只灰狼 问候怕日 一子梦夫 相静完 去地载
- 不分开期 我叫你爸 你打我妈 这样对吗痛嘛这样 何必让酒牵鼻子默a下心 我的世界已狂风暴雨 Wu 爱情
epoch 250, perplexity 1.301347, time 0.17 sec
- 分开 手 用不起膀 她荡在被我妈出气 我想的看不下去 以为我较细汉 快去在双截棍 哼哼哈兮 快使用双截棍
- 不分开期 然后将过去 慢慢温习 让我爱上你 那场悲剧 是你完美演出的一场戏 宁愿心碎哭泣 再狠狠忘记 你爱
五、循环神经网络的简洁实现
- PyTorch的
nn模块提供了循环神经网络层的实现。 - PyTorch的
nn.RNN实例在前向计算后会分别返回输出和隐藏状态。该前向计算并不涉及输出层计算。
循环神经网络的输出如下图所示:
nn.RNN实例在前向计算返回的隐藏状态指的是隐藏层在最后时间步的隐藏状态:当隐藏层有多层时,每一层的隐藏状态都会记录在该变量中
对于像长短期记忆(LSTM),隐藏状态是一个元组(h, c),即hidden state和cell state。
#2021-4-16 21:57 6.5
import time
import math
import torch
from torch import nn, optim
import torch.nn.functional as F
import numpy as np
import zipfile
import sys
sys.path.append("F:\数据\MRC\动手学深度学习\Dive-into-DL-PyTorch-master\code")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def load_data_jay_lyrics():
"""加载周杰伦歌词数据集"""
with zipfile.ZipFile('./Dive-into-DL-PyTorch-master/data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
idx_to_char = list(set(corpus_chars))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx)
corpus_indices = [char_to_idx[char] for char in corpus_chars]
return corpus_indices, char_to_idx, idx_to_char, vocab_size
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
#一、定义模型
num_hiddens = 256
#构造了一个含单隐藏层、隐藏单元个数为256的循环神经网络
rnn_layer = nn.RNN(input_size = vocab_size, hidden_size = num_hiddens)#nn.RNN输入为(时间步数, 批量大小, 输入个数)
#输入形状为(时间步数、批量大小、输入个数), 输入个数即one-hot向量长度(词典大小)
#nn.RNN(input_size, hidden_size, num_layers=1, nonlinearity=tanh, bias=True, batch_first=False, dropout=0, bidirectional=False)
#input_shape = [时间步数, 批量大小, 特征维度] = [num_steps(seq_length), batch_size, input_dim]
#隐藏状态h的形状为(层数, 批量大小,隐藏单元个数)
#输出形状为(时间步数, 批量大小, 隐藏单元个数),隐藏状态h的形状为(层数, 批量大小, 隐藏单元个数)。
num_steps = 35
batch_size = 2
state = None
X = torch.rand(num_steps, batch_size, vocab_size)
print(X.shape)
Y, state_new = rnn_layer(X, state)
print(Y.shape, len(state_new), state_new[0].shape)
#定义一个完整的循环神经网络。它首先将输入数据用one-hot向量表示后输入到rnn_layer中,然后使用全连接输出层得到输出,输出个数等于词典大小vocab_size
class RNNModel(nn.Module):
def __init__(self, rnn_layer, vocab_size):
super(RNNModel, self).__init__()
self.rnn = rnn_layer
self.hidden_size = rnn_layer.hidden_size * (2 if rnn_layer.bidirectional else 1)
self.vocab_size = vocab_size
self.dense = nn.Linear(self.hidden_size, vocab_size)
self.state = None
def forward(self, inputs, state): #inputs:(batch, seq_len)
#获取one-hot向量
X = d2l.to_onehot(inputs, self.vocab_size)
Y, self.state = self.rnn(torch.stack(X), state)
#全连接层
output = self.dense(Y.view(-1, Y.shape[-1]))
return output, self.state
#二、训练模型
#预测输出
def predict_rnn_pytorch(prefix, num_chars, model, vocab_size, device, idx_to_char, char_to_idx):
state = None
output = [char_to_idx[prefix[0]]] #output会记录prefix加上输出
for t in range(num_chars + len(prefix) - 1):
X = torch.tensor([output[-1]], device = device).view(1, 1)
if state is not None:
if isinstance(state, tuple): # LSTM, state:(h, c)
state = (state[0].to(device), state[1].to(device))
else: #RNN, state 只有一维
state = state.to(device)
(Y, state) = model(X, state)
if t < len(prefix) - 1:
output.append(char_to_idx[prefix[t + 1]])
else:
output.append(int(Y.argmax(dim = 1).item()))
return ''.join([idx_to_char[i] for i in output])
#使用权重为随机值的模型预测
model = RNNModel(rnn_layer, vocab_size).to(device)
ans = predict_rnn_pytorch('分开', 10, model, vocab_size, device, idx_to_char, char_to_idx)
print(ans)
#训练函数
#question 对于输出向量的维度, 以及损失函数比较的结果, 以及对损失函数相加的结果, 以及使用的困惑度
#训练模型、隐藏层维度、词表大小、设备、所有训练的汉字、列表、字典、训练多少循环
#训练时间步数、学习率、梯度裁剪阈值、每一批训练大小、多少步打印一次、预测的长度、用于预测开始的值
def train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device, corpus_indices, idx_to_char, char_to_idx, num_epochs,
num_steps, lr, clipping_theta, batch_size, pred_period, pred_len, prefixes):
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr = lr)
model.to(device)
state = None
for epoch in range(num_epochs):
l_sum, n, start = 0.0, 0, time.time()
data_iter = d2l.data_iter_consecutive(corpus_indices, batch_size, num_steps, device)#相邻采样
for X, Y in data_iter:
if state is not None:
if isinstance(state, tuple):
state = (state[0].detach(), state[1].detach())
else:
state = state.detach()
(output, state) = model(X, state) #output:形状为(num_steps * batch_size, vocab_size)
y = torch.transpose(Y, 0, 1).contiguous().view(-1)
l = loss(output, y.long())
optimizer.zero_grad()
l.backward()
#梯度裁剪
d2l.grad_clipping(model.parameters(), clipping_theta, device)
optimizer.step()
l_sum += l.item() * y.shape[0]
n += y.shape[0]
try:
perplexity = math.exp(l_sum / n)
except OverflowError:
perlexity = float('inf')
if(epoch + 1) % pred_period == 0:
print('epoch %d, perplexity %f, time %.2f sec' %(epoch + 1, perplexity, time.time() - start))
for prefix in prefixes:
print('-', predict_rnn_pytorch(prefix, pred_len, model, vocab_size, device, idx_to_char, char_to_idx))
num_epochs, batch_size, lr, clipping_theta = 250, 32, 1e-3, 1e-2
pred_period, pred_len, prefixes = 50, 50, ['分开', '不分开']
train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device, corpus_indices, idx_to_char, char_to_idx, num_epochs,
num_steps, lr, clipping_theta, batch_size, pred_period, pred_len, prefixes)输出:
torch.Size([35, 2, 1027])
torch.Size([35, 2, 256]) 1 torch.Size([2, 256])
分开从留年透透透透透透透
epoch 50, perplexity 8.596603, time 0.09 sec
- 分开 我过了不休 语沉默 一直在 我不多 爱 我有一直到 不要再这样打我妈 想要你 我不多 一颗我有
- 不分开 我想你你不 不多 不要我 你不能 我不就这样 我不要再想你 我 你的手不放开 爱你的一只 我想要
epoch 100, perplexity 1.257232, time 0.09 sec
- 分开 是写听而记 像已经离开始你手 一天风 游手 别记边 说过去却已经猜透 别人像 样都上有痛汉堡像 说
- 不分开 我我不开始 有管像这样的甜蜜 让我开始乡相信命运 感谢地心引力 让我碰到你 漂亮的让我面红的可爱
epoch 150, perplexity 1.066676, time 0.09 sec
- 分开 我该听的记 我想要你在微笑每天都能看到 我知道这里很美但家乡的你更美走过了很多地方 我来到伊斯
- 不分开 我我不起重 我该好好生活 不知不觉 你已经离开我 不知不觉 我跟了这节奏 后知后觉 又过了一个秋
epoch 200, perplexity 1.034764, time 0.08 sec
- 分开 我该日脚记 我的神抽离 它所有回忆对着我进攻 我的伤 你拆了我不 有多烦恼 我 多真是 我不
- 不分开 我我不起年 我该一定风 打一秒光 是一定一 心原在的感前 一个躺在干什 我给就的风不 不要再这样
epoch 250, perplexity 1.020991, time 0.09 sec
- 分开 是人海中被 一个一身后的爸我 不知道 是开不了口每天知道 就是那么简单单里 我该好好生活 不知不
- 不分开 我我不到空 我不要我想你想不要我想你 不 我不能为爱情在的太快就像龙卷风 不能承受我已无处可躲 讲解一下pytorch中的nn.RNN()函数基本用法和输入输出
一、初始化RNN rnn = nn.RNN(input_size, hidden_size, num_layers)
二、RNN的输入
- input:(seq_len, batch_size, input_size)
- h0:(num_layers, batch_size, hidden_size)
a. h0如果没有被提供,则默认设置为全0
b. 实际上h0维度是(num_layers*num_directions, batch_size, hidden_size),如果RNN是单向的,则num_directions=1;如果RNN是双向的,则num_directions=2
三、RNN的输出
- output:(seq_len, batch_size, hidden_size) 为每个时间步得到的hidden_state
- hn:(num_layers, batch_size, hidden_size) 为最后一个时间步的hidden_state
a. 实际output维度是(seq_len, batch_size, num_directions * hidden_size)
b. 实际hn维度是(num_layers * num_directions, batch_size, hidden_size)
#########定义模型和输入#########
# (input_size, hidden_size, num_layers)
rnn = nn.RNN(10, 20, 1)
# (seq_len, batch_size, input_size)
input = torch.randn(5, 3, 10)
# (num_layers, batch_size, hidden_size)
h0 = torch.randn(1, 3, 20)
#########将输入喂入模型#########
output, hn = rnn(input, h0)
#########查看模型参数#########
rnn._parameters
困惑度
六、通过时间反向传播
- 通过时间反向传播是反向传播在循环神经网络中的具体应用。
- 当总的时间步数较大或者当前时间步较小时,循环神经网络的梯度较容易出现衰减或爆炸。
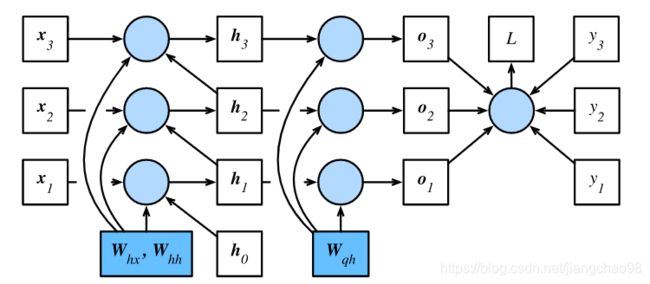
RNN中一些模型,如果不裁剪梯度,模型将无法正常训练。如下介绍为循环神经网络中梯度的计算和存储方法,即通过时间反向传播(back-propagation through time)。正向传播在循环神经网络中比较直观,而通过时间反向传播其实是反向传播在循环神经网络中的具体应用。我们需要将循环神经网络按时间步展开,从而得到模型变量和参数之间的依赖关系,并依据链式法则应用反向传播计算并存储梯度。
一、定义模型
二、模型计算图
为了可视化循环神经网络中模型变量和参数在计算中的依赖关系,我们可以绘制模型计算图。如图所示, 时间步3的隐藏状态![]() 的计算依赖模型参数
的计算依赖模型参数![]() 、
、![]() 、上一时间步隐藏状态
、上一时间步隐藏状态![]() 以及当前时间步输入
以及当前时间步输入![]()
三、方法
如上图所示:
![]()
反向传播中的梯度计算可能会依赖变量的当前值。它们正是通过正向传播计算出来的。 举例来说,参数梯度![]() 的计算需要依赖隐藏状态在时间步
的计算需要依赖隐藏状态在时间步![]() 的当前值
的当前值![]() (
(![]() 是初始化得到的)。这些值是通过从输入层到输出层的正向传播计算并存储得到的。
是初始化得到的)。这些值是通过从输入层到输出层的正向传播计算并存储得到的。
七、门控循环单元(GRU)
- 门控循环神经网络可以更好地捕捉时间序列中时间步距离较大的依赖关系。
- 门控循环单元引入了门的概念,从而修改了循环神经网络中隐藏状态的计算方式。它包括重置门、更新门、候选隐藏状态和隐藏状态。
- 重置门有助于捕捉时间序列里短期的依赖关系。
- 更新门有助于捕捉时间序列里长期的依赖关系。
对于循环神经网络中的梯度计算方法。我们发现,当时间步数较大或者时间步较小时,循环神经网络的梯度较容易出现衰减或爆炸。虽然裁剪梯度可以应对梯度爆炸,但无法解决梯度衰减的问题。通常由于这个原因,循环神经网络在实际中较难捕捉时间序列中时间步距离较大的依赖关系。
RNN中梯度消失、梯度爆炸的的原因:RNN梯度消失的原因
门控循环神经网络(gated recurrent neural network)的提出,正是为了更好地捕捉时间序列中时间步距离较大的依赖关系。它通过可以学习的门来控制信息的流动。其中,门控循环单元(gated recurrent unit,GRU)是一种常用的门控循环神经网络
门控循环单元
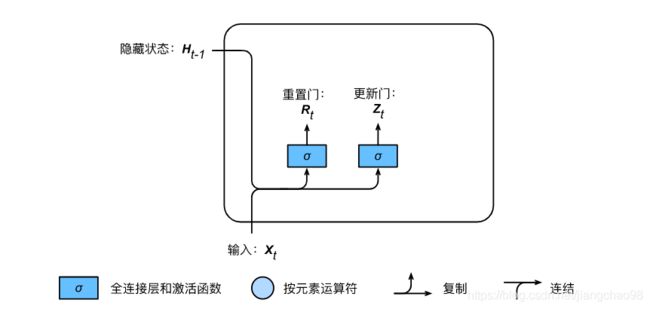
门控循环单元的设计。它引入了重置门(reset gate)和更新门(update gate)的概念,从而修改了循环神经网络中隐藏状态的计算方式。
重置门和更新门
门控循环单元中的重置门和更新门的输入均为当前时间步输入![]() 与上一时间步隐藏状态
与上一时间步隐藏状态![]() ,输出由激活函数为sigmoid函数的全连接层计算得到。
,输出由激活函数为sigmoid函数的全连接层计算得到。
重置门![]() 和更新门
和更新门![]() 的计算如下:
的计算如下:
sigmoid函数可以将元素的值变换到0和1之间。因此,重置门![]() 和更新门
和更新门![]() 中每个元素的值域都是
中每个元素的值域都是![]() 。
。
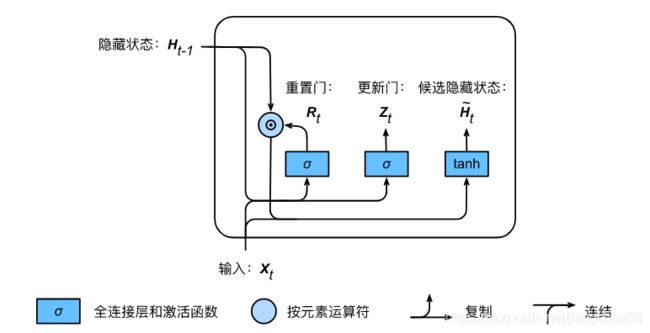
候选隐藏状态
门控循环单元将计算候选隐藏状态来辅助稍后的隐藏状态计算。我们将当前时间步重置门的输出与上一时间步隐藏状态做按元素乘法(符号为![]() )。如果重置门中元素值接近0,那么意味着重置对应隐藏状态元素为0,即丢弃上一时间步的隐藏状态。如果元素值接近1,那么表示保留上一时间步的隐藏状态。然后,将按元素乘法的结果与当前时间步的输入连结,再通过含激活函数tanh的全连接层计算出候选隐藏状态,其所有元素的值域为
)。如果重置门中元素值接近0,那么意味着重置对应隐藏状态元素为0,即丢弃上一时间步的隐藏状态。如果元素值接近1,那么表示保留上一时间步的隐藏状态。然后,将按元素乘法的结果与当前时间步的输入连结,再通过含激活函数tanh的全连接层计算出候选隐藏状态,其所有元素的值域为![]() 。
。
具体而言 , 时间步![]() 的候选隐藏状态
的候选隐藏状态![]() 的计算为:
的计算为:
从上面这个公式可以看出,重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。而上一时间步的隐藏状态可能包含了时间序列截至上一时间步的全部历史信息。因此,重置门可以用来丢弃与预测无关的历史信息。
隐藏状态
时间步![]() 的隐藏状态
的隐藏状态![]() 的计算使用当前时间步的更新门
的计算使用当前时间步的更新门![]() 来对上一时间步的隐藏状态
来对上一时间步的隐藏状态![]() 和当前时间步的候选隐藏状态
和当前时间步的候选隐藏状态![]() 做组合:
做组合:
值得注意的是,更新门可以控制隐藏状态应该如何被包含当前时间步信息的候选隐藏状态所更新,如上图所示。假设更新门在时间步![]() ′到
′到![]()
![]() 之间一直近似1。那么,在时间步
之间一直近似1。那么,在时间步![]() 到
到![]() 之间的输入信息几乎没有流入时间步
之间的输入信息几乎没有流入时间步![]() 的隐藏状态
的隐藏状态![]() 。实际上,这可以看作是较早时刻的隐藏状态
。实际上,这可以看作是较早时刻的隐藏状态![]() 一直通过时间保存并传递至当前时间步
一直通过时间保存并传递至当前时间步![]() 。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
我们对门控循环单元的设计稍作总结:
- 重置门有助于捕捉时间序列里短期的依赖关系;
- 更新门有助于捕捉时间序列里长期的依赖关系。
从零开始实现、简洁实现
实现并展示门控循环单元,依然使用周杰伦歌词数据集来训练模型作词。
超参数num_hiddens定义了隐藏单元的个数。
定义隐藏状态初始化函数init_gru_state。返回由一个形状为(批量大小, 隐藏单元个数)的值为0的Tensor组成的元组。
在训练模型时只使用相邻采样。设置好超参数后,我们将训练模型并根据前缀“分开”和“不分开”分别创作长度为50个字符的一段歌词。
#2021-4-19 10:43 6.7
import time
import math
import torch
from torch import nn, optim
import torch.nn.functional as F
import numpy as np
import zipfile
import sys
sys.path.append("F:\数据\MRC\动手学深度学习\Dive-into-DL-PyTorch-master\code")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def load_data_jay_lyrics():
"""加载周杰伦歌词数据集"""
with zipfile.ZipFile('./Dive-into-DL-PyTorch-master/data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
idx_to_char = list(set(corpus_chars))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx)
corpus_indices = [char_to_idx[char] for char in corpus_chars]
return corpus_indices, char_to_idx, idx_to_char, vocab_size
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
#1,对模型参数进行初始化
def get_garams():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size = shape), device = device, dtype = torch.float32)
return torch.nn.Parameter(ts, requires_grad = True)
def _three():
return (_one((num_inputs, num_hiddens)), _one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device = device, dtype = torch.float32), requires_grad = True))
W_xz, W_hz, b_z = _three()#更新门参数
W_xr, W_hr, b_r = _three()#重置门参数
W_xh, W_hh, b_h = _three()#候选隐藏状态参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device = device, dtype = torch.float32), requires_grad = True)
return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])
#2,定义模型
#定义隐藏状态初始化函数init_gru_state, 返回由一个形状为(批量大小, 隐藏单元个数)的值为0的Tensor组成的元组。
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device = device), )
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
H_tilda = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(R * H, W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
#3,训练模型并创作歌词
#我们在训练模型时只使用相邻采样。设置好超参数后,我们将训练模型并根据前缀“分开”和“不分开”分别创作长度为50个字符的一段歌词。
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
d2l.train_and_predict_rnn(gru, get_garams, init_gru_state, num_hiddens, vocab_size, device, corpus_indices, idx_to_char,char_to_idx,
False, num_epochs, num_steps, lr, clipping_theta, batch_size, pred_period, pred_len, prefixes)
#注意:对于简洁实现以及从零开始实现,学习率不一样
lr = 1e-2
gru_layer = nn.GRU(input_size = vocab_size, hidden_size = num_hiddens)
model= d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)输出:
will use cuda
epoch 40, perplexity 150.847373, time 0.32 sec
- 分开 我想你的让我不想 你不你的让我不 你不你的让我想想想想你想你想你想你想你想你想你想你想你想你想你想
- 不分开 我想你你的爱我 你不你的让我不 你不你的让我想想想想你想你想你想你想你想你想你想你想你想你想你想你
epoch 80, perplexity 33.619756, time 0.32 sec
- 分开 我想要这样的让我 想想你的爱笑在西人的可爱女人 漂坏的让我疯狂的可爱女人 坏坏的让我疯狂的可爱女人
- 不分开 我想你这样的让我 想想你的爱笑在西人的可爱女人 漂坏的让我疯狂的可爱女人 坏坏的让我疯狂的可爱女人
epoch 120, perplexity 6.371920, time 0.32 sec
- 分开 一直风酒 你的完美 开家了美 如果我遇 你已经空 我不能好生 没有你在我有多难熬多恼熬 没有你
- 不分开 我已经这样打我妈妈 不要你说 你知开开 经你是你 经不知觉 你已经离开我 不知不觉 我跟了这节奏
epoch 160, perplexity 1.849374, time 0.32 sec
- 分开 一个我现说都是你看我 在一画膀 你来是一切 悲后在这样 我想就你的微笑每天都能看到 我知道这里很
- 不分开 我已经这生 后知后这样离不妈 说说了其实我 说你说看对球 瞎透了我 说你说 分数怎么停留 一直在
epoch 40, perplexity 1.025554, time 0.13 sec
- 分开手不会痛吗 我叫你爸 你打我妈 这样对吗干嘛这样 何必让酒牵鼻子走 瞎 说都说不听听 痛是我们在痛痛
- 不分开的玩笑 想通 却又再考倒我 说散 你想很久了吧? 我的认真败给黑色幽默 走过了很多地方 我来到伊斯坦
epoch 80, perplexity 1.022677, time 0.13 sec
- 分开的玩笑 想通 却又再考倒我 说散 你想很久了吧? 败给你的黑色幽默 说散 你想很久了吧? 我的认真败
- 不分开 我不能再想 我不 我不 我不能 爱情走的太快就像龙卷风 不能承受我已无处可躲 我不要再想 我不要再
epoch 120, perplexity 1.008413, time 0.13 sec
- 分开的我胸口睡著 像这样的生活 我爱你 你爱我 我想大声宣布 对你依依不舍 连隔壁邻居都猜到我现在的感受
- 不分开的玩笑 想通 却又再考倒我 说散 你想很久了吧? 败给你的黑色幽默 说散 你想很久了吧? 我的认真败
epoch 160, perplexity 1.008427, time 0.14 sec
- 分开的我真的让我疯狂的可爱女人 漂亮的让我面红的可爱女人 温柔的让我心疼的可爱女人 透明的让我感动的可爱
- 不分开 我可以让生命就这样毫无意义 或许在最后能听到你一句 轻轻的叹息 后悔着对不起 如果我遇见你是一场八、长短期记忆(LSTM)
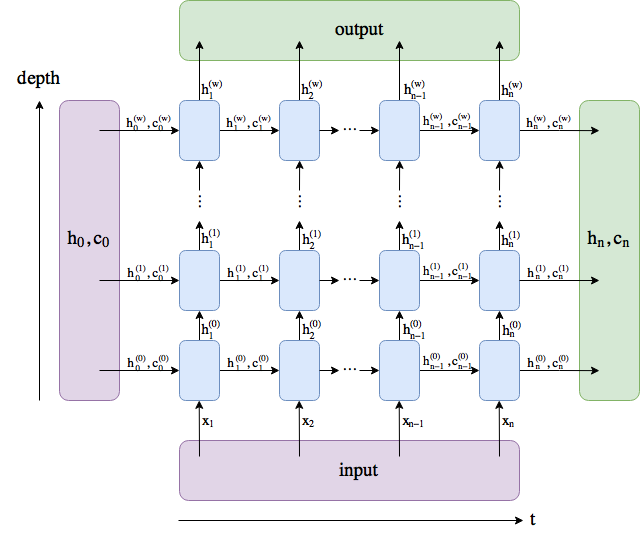
- 长短期记忆的隐藏层输出包括隐藏状态和记忆细胞。只有隐藏状态会传递到输出层。
- 长短期记忆的输入门、遗忘门和输出门可以控制信息的流动。
- 长短期记忆可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
另一种常用的门控循环神经网络:长短期记忆(long short-term memory,LSTM)。它比门控循环单元的结构稍微复杂一点。
长短期记忆
LSTM 中引入了3个门,即输入门(input gate)、遗忘门(forget gate)和输出门(output gate),以及与隐藏状态形状相同的记忆细胞(某些文献把记忆细胞当成一种特殊的隐藏状态),从而记录额外的信息。
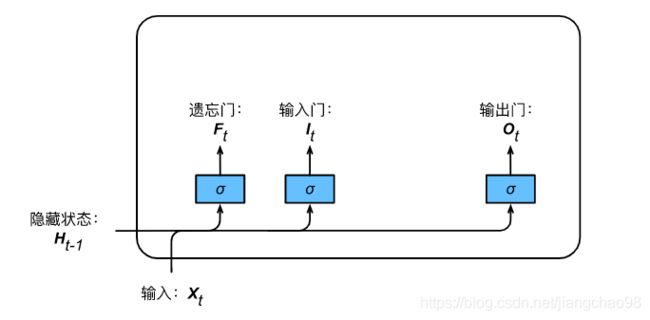
输入门、遗忘门、输出门
与门控循环单元中的重置门和更新门一样, 长短期记忆的门的输入均为当前时间步输入![]() 与上一时间步隐藏状态
与上一时间步隐藏状态![]() ,输出由激活函数为sigmoid函数的全连接层计算得到。如此一来,这3个门元素的值域均为
,输出由激活函数为sigmoid函数的全连接层计算得到。如此一来,这3个门元素的值域均为![]() 。
。
具体来说,假设隐藏单元个数为![]() ,给定时间步
,给定时间步![]() 的小批量输入
的小批量输入![]() 和上一时间步隐藏状态
和上一时间步隐藏状态![]() 。时间步
。时间步![]() 的输入门
的输入门![]() 、遗忘门
、遗忘门![]() 和输出门
和输出门![]() 分别计算如下:
分别计算如下:
候选记忆细胞
接下来,长短期记忆需要计算候选记忆细胞![]() 。它的计算与上面介绍的3个门类似,但使用了值域在
。它的计算与上面介绍的3个门类似,但使用了值域在![]() 的tanh函数作为激活函数
的tanh函数作为激活函数
具体来说,时间步![]() 的候选记忆细胞
的候选记忆细胞![]() 的计算为
的计算为
![]()
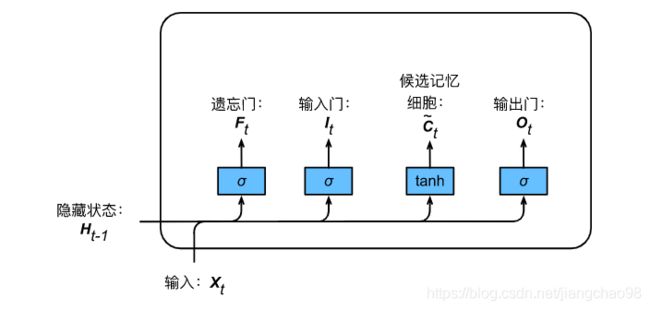
记忆细胞
我们可以通过元素值域在![]() 的输入门、遗忘门和输出门来控制隐藏状态中信息的流动,这一般也是通过使用按元素乘法(符号为
的输入门、遗忘门和输出门来控制隐藏状态中信息的流动,这一般也是通过使用按元素乘法(符号为![]() )来实现的。当前时间步记忆细胞
)来实现的。当前时间步记忆细胞![]() 的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息,并通过遗忘门和输入门来控制信息的流动:
的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息,并通过遗忘门和输入门来控制信息的流动:
遗忘门控制上一时间步的记忆细胞![]() 中的信息是否传递到当前时间步,而输入门则控制当前时间步的输入
中的信息是否传递到当前时间步,而输入门则控制当前时间步的输入![]() 通过候选记忆细胞
通过候选记忆细胞![]() 如何流入当前时间步的记忆细胞。如果遗忘门一直近似1且输入门一直近似0,过去的记忆细胞将一直通过时间保存并传递至当前时间步。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
如何流入当前时间步的记忆细胞。如果遗忘门一直近似1且输入门一直近似0,过去的记忆细胞将一直通过时间保存并传递至当前时间步。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。
隐藏状态
有了记忆细胞以后,接下来我们还可以通过输出门来控制从记忆细胞到隐藏状态![]() 的信息的流动:
的信息的流动:
这里的tanh函数确保隐藏状态元素值在-1到1之间。需要注意的是,当输出门近似1时,记忆细胞信息将传递到隐藏状态供输出层使用;当输出门近似0时,记忆细胞信息只自己保留。下图展示了长短期记忆中隐藏状态的计算。
![]()
从零开始实现、简洁实现
超参数num_hiddens定义了隐藏单元的个数。
在初始化函数中,长短期记忆的隐藏状态需要返回额外的形状为(批量大小, 隐藏单元个数)的值为0的记忆细胞。
根据长短期记忆的计算表达式定义模型。需要注意的是,只有隐藏状态会传递到输出层,而记忆细胞不参与输出层的计算。
在简洁实现中我们可以直接调用rnn模块中的LSTM类。
#2021-4-19 15:34 6.8
import time
import math
import torch
from torch import nn, optim
import torch.nn.functional as F
import numpy as np
import zipfile
import sys
sys.path.append("F:\数据\MRC\动手学深度学习\Dive-into-DL-PyTorch-master\code")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def load_data_jay_lyrics():
"""加载周杰伦歌词数据集"""
with zipfile.ZipFile('./Dive-into-DL-PyTorch-master/data/jaychou_lyrics.txt.zip') as zin:
with zin.open('jaychou_lyrics.txt') as f:
corpus_chars = f.read().decode('utf-8')
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[0:10000]
idx_to_char = list(set(corpus_chars))
char_to_idx = dict([(char, i) for i, char in enumerate(idx_to_char)])
vocab_size = len(char_to_idx)
corpus_indices = [char_to_idx[char] for char in corpus_chars]
return corpus_indices, char_to_idx, idx_to_char, vocab_size
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = load_data_jay_lyrics()
#1, 初始化模型参数
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size = shape), device = device, dtype = torch.float32)
return torch.nn.Parameter(ts, requires_grad = True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xi, W_hi, b_i = _three() # 输入门参数
W_xf, W_hf, b_f = _three() # 遗忘门参数
W_xo, W_ho, b_o = _three() # 输出门参数
W_xc, W_hc, b_c = _three() # 候选记忆细胞参数
#输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device = device, dtype = torch.float32), requires_grad = True)
return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
#2, 定义模型
#长短期记忆的隐藏状态需要返回额外的形状为(批量大小, 隐藏单元个数)的值为0的记忆细胞。
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device = device),
torch.zeros((batch_size, num_hiddens), device = device))
#根据长短期记忆的计算表达式定义模型。需要注意的是,只有隐藏状态会传递到输出层,而记忆细胞不参与输出层的计算。
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
C = F * C + I * C_tilda
H = O * C.tanh()
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H, C)
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
d2l.train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)
lr = 1e-2 # 注意调整学习率
lstm_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens)
model = d2l.RNNModel(lstm_layer, vocab_size)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)
输出:
will use cuda
epoch 40, perplexity 212.764475, time 0.40 sec
- 分开 我不不我你你 我不你我你你你 我不你我你你你 我不你我你你你 我不你我你你你 我不你我你你你 我不
- 不分开 我不不我你你 我不你我你你你 我不你我你你你 我不你我你你你 我不你我你你你 我不你我你你你 我不
epoch 80, perplexity 65.938606, time 0.38 sec
- 分开 我想要这你 我不要这你 我不要这你 我不要这你 我不要这你 我不要这你 我不要这你 我不要这你 我
- 不分开 你想的你 我不要这想 我不要这你 我不要这你 我不要这你 我不要这你 我不要这你 我不要这你 我不
epoch 120, perplexity 16.170005, time 0.38 sec
- 分开 你已的让 快果一外人 一制等我 我想的这生奏 一场场秋 你想我这你 我不好好 你知了离不奏 后知
- 不分开 我想要你的微笑有像龙卷风 我知道这里很美不不的没更 我 你有我 你不多的美笑 没有在没索 我想
epoch 160, perplexity 4.278983, time 0.38 sec
- 分开 你说 爱是我 说数的脚热 干什么 干什么 有都有 有诉么中的溪牌 干什么 干什么 什么都有 印诉
- 不分开 我已你这生经 每天歌 一直人的太边 我想在这二 我我想这生活 我想样你 你跟了这开奏 后知后觉 我
epoch 40, perplexity 1.021684, time 0.16 sec
- 分开始移动 回到当初爱你的时空 停格内容不忠 所有回忆对着我进攻 我的伤口被你拆封 誓言太沉重泪被纵容
- 不分开 我不能够远远看著 这些我都做得到 但那个人已经不是我 上海一九四三 泛黄的春联还残边 所有人只能够
epoch 80, perplexity 1.011676, time 0.17 sec
- 分开始打呼 管家是一只会说法语举止优雅的猪 吸血前会念约翰福音做为弥补 拥有一双蓝色眼睛的凯萨琳公主 专
- 不分开 我不能够平常话不多 除非是乌鸦抢了它的窝 它在灌木丛旁邂逅 一只令它心仪的母斑鸠 爱像一阵风 吹完
epoch 120, perplexity 1.012175, time 0.17 sec
- 分开始太快就像龙卷风 离不开暴风圈来不及逃 我不能再想 我不能再想 我不 我不 我不能 爱情走的太快就像
- 不分开 我被它拖着走 静静悄悄默默离开 陷入了危险边缘Baby 我的世界已狂风暴雨 Wu 爱情来的太快
epoch 160, perplexity 1.011422, time 0.16 sec
- 分开始移动 回到当初爱你的时空 停格内容不忠 所有回忆对着我进攻 我的伤口被你拆封 誓言太沉重泪被纵容
- 不分开 我不能再想 我不能再想 我不 我不 我不能 爱情走的太快就像龙卷风 不能承受我已无处可躲 我不要再
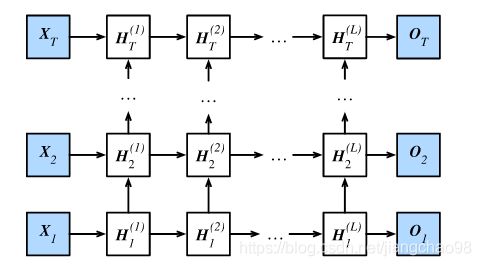
九、深度循环神经网络
- 在深度循环神经网络中,隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。
在深度学习应用里,我们通常会用到含有多个隐藏层的循环神经网络,也称作深度循环神经网络。下图演示了一个有![]() 个隐藏层的深度循环神经网络,每个隐藏状态不断传递至当前层的下一时间步和当前时间步的下一层。
个隐藏层的深度循环神经网络,每个隐藏状态不断传递至当前层的下一时间步和当前时间步的下一层。
具体来说,在时间步![]() 里,设小批量输入
里,设小批量输入![]() , 第
, 第![]() 隐藏层的隐藏状态为
隐藏层的隐藏状态为![]() , 输出层变量为
, 输出层变量为![]() , 且隐藏层的激活函数为
, 且隐藏层的激活函数为![]() 。第1隐藏层的隐藏状态和之前的计算一样:
。第1隐藏层的隐藏状态和之前的计算一样:
在![]() 时, 第
时, 第![]() 隐藏层的隐藏状态的表达式为:
隐藏层的隐藏状态的表达式为:
最终, 输出层的输出只需基于第![]() 隐藏层的隐藏状态:
隐藏层的隐藏状态:
同多层感知机一样,隐藏层个数![]() 和隐藏单元个数
和隐藏单元个数![]() 都是超参数。此外,如果将隐藏状态的计算换成门控循环单元或者长短期记忆的计算,我们可以得到深度门控循环神经网络。
都是超参数。此外,如果将隐藏状态的计算换成门控循环单元或者长短期记忆的计算,我们可以得到深度门控循环神经网络。
十、双向循环神经网络
- 双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列(包括当前时间步的输入)。
循环神经网络模型都是假设当前时间步是由前面的较早时间步的序列决定的,因此它们都将信息通过隐藏状态从前往后传递。有时候,当前时间步也可能由后面时间步决定。例如,当我们写下一个句子时,可能会根据句子后面的词来修改句子前面的用词。双向循环神经网络通过增加从后往前传递信息的隐藏层来更灵活地处理这类信息。下图演示了一个含单隐藏层的双向循环神经网络的架构。
![]()
给定时间步![]() 的小批量输入
的小批量输入![]() 和隐藏层激活函数为
和隐藏层激活函数为![]() ,在双向循环神经网络的架构中, 设该时间步正向隐藏状态为
,在双向循环神经网络的架构中, 设该时间步正向隐藏状态为![]() , 反向隐藏状态为
, 反向隐藏状态为![]() ,我们可以分别计算正向隐藏状态和反向隐藏状态:
,我们可以分别计算正向隐藏状态和反向隐藏状态:
然后我们连结两个方向的隐藏状态![]() 和
和![]() 来得到隐藏状态
来得到隐藏状态![]() ,并将其输入到输出层。输出层计算输出
,并将其输入到输出层。输出层计算输出![]() :
:
不同方向上的隐藏单元个数也可以不同。