【转载】细嚼慢咽读论文：PointNet论文及代码详细解析

文章转载自知乎

论文标题：PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation

标签：有监督 | 特征学习、点云分类、语义分割

---

首先回答3个问题作为引子：

Q1：什么是点云？

简单来说就是一堆三维点的集合，必须包括各个点的三维坐标信息，其他信息比如各个点的法向量、颜色等均是可选。

点云的文件格式可以有很多种，包括xyz，npy，ply，obj，off等（有些是mesh不过问题不大，因为mesh可以通过泊松采样等方式转化成点云）。对于单个点云，如果你使用np.loadtxt得到的实际上就是一个维度为 （num_points, num_channels） 的张量，num_channels一般为3，表示点云的三维坐标。 

这里以horse.xyz文件为例，实际就是文本文件，打开后数据长这样（局部，总共有2048个点）：

实际就是一堆点的信息，这里只有三维坐标，将其可视化出来长这样：

Q2：为什么点云处理任务是重要的？

三维图形具有多种表现形式，包括了mesh、体素、点云等，甚至还有些方法使用多视图来对三维图形表征。而点云在以上各种形式的数据中算是日常生活中最能够大规模获取和使用的数据结构了，包括自动驾驶、增强现实等在内的应用需要直接或间接从点云中提取信息，点云处理也逐渐成为计算机视觉非常重要的一部分。

Q3：为什么PointNet是重要的？

这个后面会说，直接对点云使用深度学习、解决了点云带来的一系列挑战，PointNet应该是开创性的。但我觉得，真正让PointNet具备很大影响力的，还是它的简洁、高效和强大。

---

首先要说清楚，PointNet所作的事情就是对点云做特征学习，并将学习到的特征去做不同的应用：分类（shape-wise feature）、分割（point-wise feature）等。

PointNet之所以影响力巨大，就是因为它为点云处理提供了一个简单、高效、强大的特征提取器（encoder），几乎可以应用到点云处理的各个应用中，其地位类似于图像领域的AlexNet。

---

1 motivation

related work

1. Volumetric CNNs：对体素应用3DCNN。缺点是点云的坐标空间的稀疏性导致转成体素后的分辨率问题，以及3D卷积带来的开销。
2. Multiview CNNs：将点云或者shape渲染成视图，使用传统的图像卷积来做特征学习。这种方法确实取得了不错的效果，但是缺点是应用非常局限，像分割、补全等任务就不太好做。
3. Spectral CNNs
4. feature-based DNN

why we want to do this?

点云或者mesh，大多数研究人员都是将其转化成3D体素或者多视图来做特征学习的，这其中的工作包括了VoxelNet, MVCNN等。这些工作都或多或少存在了一些问题（上面提到了）。

直接对点云做特征学习也不是不可以，但有几个问题需要考虑：特征学习需要对点云中各个点的排列保持不变性、特征学习需要对rigid transformation保持不变性等。虽然有挑战，但是深度学习强大的表征能力以及其在图像领域取得的巨大成功，因此是很有必要直接在点云上进行尝试的。

2 contribution

1. 我们设计了一个新颖的深层网络架构来处理三维中的无序点集
2. 我们设计的网络表征可以做三维图形分类、图形的局部分割以及场景的语义分割等任务
3. 我们提供了完备的经验和理论分析来证明PointNet的稳定和高效。
4. 充分的消融实验，证明网络各个部分对于表征的有效性。

3 solution

3.1 challenges

点云的几个特点：

1. 无序性 --> 对称函数设计用于表征
2. 点不是孤立的，需要考虑局部结构 --> 局部全局特征结合
3. 仿射变换无关性 --> alignment network

forward propagation

PointNet网络结构图

网络分成了分类网络和分割网络2个部分，大体思路类似，都是设计表征的过程：

分类网络设计global feature，分割网络设计point-wise feature

两者都是为了让表征尽可能discriminative，也就是同类的能分到一类，不同类的距离能拉开

PointNet设计思路主要有以下3点：

1、Symmetry Function for Unordered Input：

要做到对点云点排列不变性有几种思路：

1、直接将点云中的点以某种顺序输入（比如按照坐标轴从小到大这样）

为什么不这样做？（摘自原文）in high dimensional space there in fact does not exist an ordering that is stable w.r.t. point perturbations in the general sense.简单来说就是很难找到一种稳定的排序方法

2、作为序列去训练一个RNN，即使这个序列是随机排布的，RNN也有能力学习到排布不变性。

为什么不这样做？（摘自原文）While RNN has relatively good robustness to input ordering for sequences with small length (dozens), it’s hard to scale to thousands of input elements, which is the common size for point sets. RNN很难处理好成千上万长度的这种输入元素（比如点云）。

3、使用一个简单的对称函数去聚集每个点的信息

我们的目标：左边 f 是我们的目标，右边 g 是我们期望设计的对称函数。由上公式可以看出，基本思路就是对各（每）个元素（即点云中的各（每）个点）使用 h 分别处理，在送入对称函数 g 中处理，以实现排列不变性。

在实现中 h 就是MLP， g 就是max pooling

对于以上三种不同的做法，作者均作了实验来验证，得出第三种方法效果最好：

2 Local and Global Information Aggregation：

对于分割任务，我们需要point-wise feature

因此分割网络和分类网络设计局部略有不同，分割网络添加了每个点的local和global特征的拼接过程，以此得到同时对局部信息和全局信息感知的point-wise特征，提升表征效果。

3 alignment network：

用于实现网络对于仿射变换、刚体变换等变换的无关性

直接的思路：将所有的输入点集对齐到一个统一的点集空间

pn的做法：直接预测一个变换矩阵（3*3）来处理输入点的坐标。因为会有数据增强的操作存在，这样做可以在一定程度上保证网络可以学习到变换无关性。

特征空间的对齐也可以这么做，但是需要注意：

transformation matrix in the feature space has much higher dimension than the spatial transform matrix, which greatly increases the difficulty of optimization. 对于特征空间的alignment network，由于特征空间维度比较高，因此直接生成的alignment matrix会维度特别大，不好优化，因此这里需要加个loss约束一下。

add a regularization term to our softmax training loss：

使得特征空间的变换矩阵A尽可能接近正交矩阵

消融实验验证alignment network的效果：

loss

看代码：分类中常用的交叉熵+alignment network中用于约束生成的alignment matrix的loss

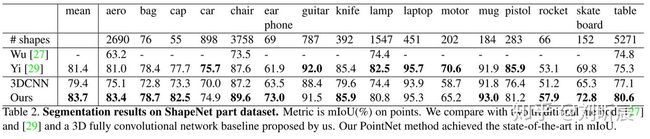
4 dataset and experiments

evaluate metric

分类：分类准确率acc
分割：mIoU

dataset

分类：ModelNet40
分割：ShapeNet Part dataset和Stanford 3D semantic parsing dataset

experiments

分类：

局部分割：

5 code

看代码分析PointNet结构：

观察上图，有4个值得关注的点：
1. 如何对点云使用MLP？
2. alignment network怎么做的？
3. 对称函数如何实现来提取global feature的？
4. loss?

针对问题1：

以分类网络为例，整体代码：

def get_model(point_cloud, is_training, bn_decay=None):
    """ Classification PointNet, input is BxNx3, output Bx40 """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value
    end_points = {}
    with tf.variable_scope('transform_net1') as sc:
        transform = input_transform_net(point_cloud, is_training, bn_decay, K=3)
    point_cloud_transformed = tf.matmul(point_cloud, transform)
    input_image = tf.expand_dims(point_cloud_transformed, -1)
    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv2', bn_decay=bn_decay)
    with tf.variable_scope('transform_net2') as sc:
        transform = feature_transform_net(net, is_training, bn_decay, K=64)
    end_points['transform'] = transform
    net_transformed = tf.matmul(tf.squeeze(net, axis=[2]), transform)
    net_transformed = tf.expand_dims(net_transformed, [2])
    net = tf_util.conv2d(net_transformed, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv3', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv4', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv5', bn_decay=bn_decay)
    # Symmetric function: max pooling
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='maxpool')
    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='fc1', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp1')
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='fc2', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp2')
    net = tf_util.fully_connected(net, 40, activation_fn=None, scope='fc3')
    return net, end_points

MLP的核心做法：特征维度拓展。从N×3升维到N×64，然后64维度升级到128,1024。

input_image = tf.expand_dims(point_cloud_transformed, -1)
net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv1', bn_decay=bn_decay)
net = tf_util.conv2d(net, 64, [1,1],
                     padding='VALID', stride=[1,1],
                     bn=True, is_training=is_training,
                     scope='conv2', bn_decay=bn_decay)

这里input_image维度是，因此将点云看成是W和H分为N和3的2D图像，维度是1。 

然后直接基于这个“2D图像”做卷积，第一个卷积核size是[1, 3]，正好对应的就是“2D图像”的一行，也就是一个点（三维坐标），输出通道数(特征维度 / 卷积核个数（一个卷积核对应一个特征通道数）)是64，因此输出张量维度应该是。 

第二个卷积核size是[1, 1]，1*1卷积只改变通道数，输出张量维度是 

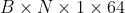
conv2d就是将卷积封装了一下，核心部分也就是调用tf.nn.conv2d，实现如下：

def conv2d(inputs,
           num_output_channels,
           kernel_size,
           scope,
           stride=[1, 1],
           padding='SAME',
           use_xavier=True,
           stddev=1e-3,
           weight_decay=0.0,
           activation_fn=tf.nn.relu,
           bn=False,
           bn_decay=None,
           is_training=None):
  """ 2D convolution with non-linear operation.
  Args:
    inputs: 4-D tensor variable BxHxWxC
    num_output_channels: int
    kernel_size: a list of 2 ints
    scope: string
    stride: a list of 2 ints
    padding: 'SAME' or 'VALID'
    use_xavier: bool, use xavier_initializer if true
    stddev: float, stddev for truncated_normal init
    weight_decay: float
    activation_fn: function
    bn: bool, whether to use batch norm
    bn_decay: float or float tensor variable in [0,1]
    is_training: bool Tensor variable
  Returns:
    Variable tensor
  """
  with tf.variable_scope(scope) as sc:
      kernel_h, kernel_w = kernel_size
      num_in_channels = inputs.get_shape()[-1].value
      kernel_shape = [kernel_h, kernel_w,
                      num_in_channels, num_output_channels]
      kernel = _variable_with_weight_decay('weights',
                                           shape=kernel_shape,
                                           use_xavier=use_xavier,
                                           stddev=stddev,
                                           wd=weight_decay)
      stride_h, stride_w = stride
      outputs = tf.nn.conv2d(inputs, kernel,
                             [1, stride_h, stride_w, 1],
                             padding=padding)
      biases = _variable_on_cpu('biases', [num_output_channels],
                                tf.constant_initializer(0.0))
      outputs = tf.nn.bias_add(outputs, biases)
      if bn:
        outputs = batch_norm_for_conv2d(outputs, is_training,
                                        bn_decay=bn_decay, scope='bn')
      if activation_fn is not None:
        outputs = activation_fn(outputs)
      return outputs

针对问题2：

这里以input_transform_net为例：

def input_transform_net(point_cloud, is_training, bn_decay=None, K=3):
    """ Input (XYZ) Transform Net, input is BxNx3 gray image
        Return:
            Transformation matrix of size 3xK """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value
    input_image = tf.expand_dims(point_cloud, -1)
    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv2', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv3', bn_decay=bn_decay)
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='tmaxpool')
    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='tfc1', bn_decay=bn_decay)
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='tfc2', bn_decay=bn_decay)
    with tf.variable_scope('transform_XYZ') as sc:
        assert(K==3)
        weights = tf.get_variable('weights', [256, 3*K],
                                  initializer=tf.constant_initializer(0.0),
                                  dtype=tf.float32)
        biases = tf.get_variable('biases', [3*K],
                                 initializer=tf.constant_initializer(0.0),
                                 dtype=tf.float32)
        biases += tf.constant([1,0,0,0,1,0,0,0,1], dtype=tf.float32)
        transform = tf.matmul(net, weights)
        transform = tf.nn.bias_add(transform, biases)
    transform = tf.reshape(transform, [batch_size, 3, K])
    return transform

实际上，前半部分就是通过卷积和max_pooling对batch内各个点云提取global feature，再将global feature降到3×K维度，并reshape成3×3，得到transform matrix。

通过数据增强丰富训练数据集，网络确实应该学习到有效的transform matrix，用来实现transformation invariance

针对问题3：

max_pooling，这个在论文的图中还是代码中都有体现，代码甚至直接用注释注明了

针对问题4：

def get_loss(pred, label, end_points, reg_weight=0.001):
    """ pred: B*NUM_CLASSES,
        label: B, """
    loss = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=pred, labels=label)
    classify_loss = tf.reduce_mean(loss)
    tf.summary.scalar('classify loss', classify_loss)
    # Enforce the transformation as orthogonal matrix
    transform = end_points['transform'] # BxKxK
    K = transform.get_shape()[1].value
    mat_diff = tf.matmul(transform, tf.transpose(transform, perm=[0,2,1]))
    mat_diff -= tf.constant(np.eye(K), dtype=tf.float32)
    mat_diff_loss = tf.nn.l2_loss(mat_diff) 
    tf.summary.scalar('mat loss', mat_diff_loss)
    return classify_loss + mat_diff_loss * reg_weight

无论是分类还是分割，本质上都还是分类任务，只是粒度不同罢了。

因此loss一定有有监督分类任务中常用的交叉熵loss

另外loss还有之前alignment network中提到的约束loss，也就是上面的mat_diff_loss

5 conclusion

PointNet之所以影响力巨大，并不仅仅是因为它是第一篇，更重要的是它的网络很简洁（简洁中蕴含了大量的工作来探寻出简洁这条路）却非常的work，这也就使得它能够成为一个工具，一个为点云表征的encoder工具，应用到更广阔的点云处理任务中。

MLP+max pooling竟然就击败了众多SOTA，令人惊讶。另外PointNet在众多细节设计也都进行了理论分析和消融实验验证，保证了严谨性，这也为PointNet后面能够大规模被应用提供了支持。