Prophet 时间序列预测

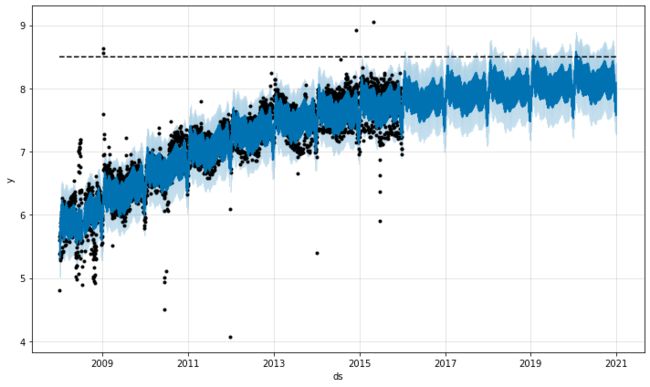
Prophet 允许使用具有指定承载能力的物流增长趋势模型进行预测。

我们必须在列中指定承载能力cap。在这里，我们将假设一个特定的值，但这通常是使用有关市场规模的数据或专业知识来设置的。

# Python df['cap'] = 8.5

需要注意的重要事项是cap必须为数据框中的每一行指定，并且它不必是常量。如果市场规模在增长，那么cap可以是一个递增的序列。然后我们像以前一样拟合模型，除了传入一个额外的参数来指定逻辑增长：

# Python
m = Prophet(growth='logistic')
m.fit(df)

# Python
future = m.make_future_dataframe(periods=1826)
future['cap'] = 8.5
fcst = m.predict(future)
fig = m.plot(fcst)

 

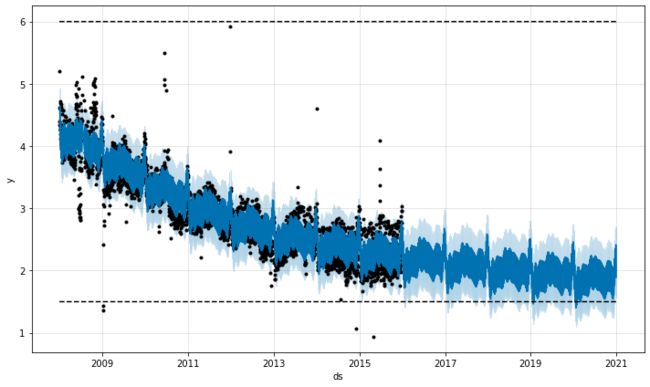
饱和最小值

逻辑增长模型还可以处理饱和最小值，用列指定的floor方式与cap列指定最大值的方式相同：

# Python
df['y'] = 10 - df['y']
df['cap'] = 6
df['floor'] = 1.5
future['cap'] = 6
future['floor'] = 1.5
m = Prophet(growth='logistic')
m.fit(df)
fcst = m.predict(future)
fig = m.plot(fcst)

 趋势变化点：

默认情况下，Prophet 指定了 25 个潜在的变化点，它们统一放置在时间序列的前 80% 中。此图中的垂直线表示放置潜在变化点的位置：

 可以使用参数 设置潜在变化点的数量n_changepoints，但通过调整正则化可以更好地调整。意义变化点的位置可以通过以下方式可视化：

# Python from prophet.plot import add_changepoints_to_plot fig = m.plot(forecast) a = add_changepoints_to_plot(fig.gca(), m, forecast)

默认情况下，只为时间序列的前 80% 推断变化点，以便有足够的跑道来预测趋势并避免时间序列末尾的过度拟合波动。此默认值适用于许多情况但不是所有情况，并且可以使用changepoint_range参数进行更改。例如，m = Prophet(changepoint_range=0.9)在 Python 或m <- prophet(changepoint.range = 0.9)R 中将在时间序列的前 90% 中放置潜在的变化点。

调整趋势灵活性

如果趋势变化过拟合（灵活性太大）或欠拟合（灵活性不够），您可以使用输入参数调整稀疏先验的强度changepoint_prior_scale。默认情况下，此参数设置为 0.05。增加它会使趋势更加灵活：

# Python
m = Prophet(changepoint_prior_scale=0.5)
forecast = m.fit(df).predict(future)
fig = m.plot(forecast)

 

# Python
m = Prophet(changepoint_prior_scale=0.001)
forecast = m.fit(df).predict(future)
fig = m.plot(forecast)

指定变更点的位置

您可以使用changepoints参数手动指定潜在变化点的位置，而不是使用自动变化点检测。然后只允许在这些点进行斜率变化，并使用与以前相同的稀疏正则化。

# Python
m = Prophet(changepoints=['2014-01-01'])
forecast = m.fit(df).predict(future)
fig = m.plot(forecast)

 季节性、假期效应和回归量

建模假期和特别活动

如果您有假期或其他要建模的重复事件，则必须为它们创建一个数据框。它有两列（holiday和ds）和一行用于假期的每次出现。它必须包括假期的所有事件，包括过去（就历史数据而言）和未来（就预测而言）。如果它们将来不再重复，Prophet 将对它们进行建模，然后不将它们包含在预测中。

您还可以包括列lower_window并将upper_window假期延长到[lower_window, upper_window]日期周围的天数。例如，如果您想在圣诞节之外还包括平安夜，您可以包括lower_window=-1,upper_window=0. 如果您想在感恩节之外使用黑色星期五，您可以包括lower_window=0,upper_window=1. 您还可以包括一个列prior_scale来为每个假期单独设置先前的比例，如下所述。

在这里，我们创建了一个包含佩顿曼宁所有季后赛出场日期的数据框：

# Python
playoffs = pd.DataFrame({
  'holiday': 'playoff',
  'ds': pd.to_datetime(['2008-01-13', '2009-01-03', '2010-01-16',
                        '2010-01-24', '2010-02-07', '2011-01-08',
                        '2013-01-12', '2014-01-12', '2014-01-19',
                        '2014-02-02', '2015-01-11', '2016-01-17',
                        '2016-01-24', '2016-02-07']),
  'lower_window': 0,
  'upper_window': 1,
})
superbowls = pd.DataFrame({
  'holiday': 'superbowl',
  'ds': pd.to_datetime(['2010-02-07', '2014-02-02', '2016-02-07']),
  'lower_window': 0,
  'upper_window': 1,
})
holidays = pd.concat((playoffs, superbowls))

# Python m = Prophet(holidays=holidays) forecast = m.fit(df).predict(future)

内置乡村假期

您可以使用add_country_holidays方法 (Python) 或函数 (R)来使用特定国家/地区假期的内置集合。指定国家/地区名称，然后除了通过上述holidays参数指定的任何假期外，还将包括该国家/地区的主要假期：

# Python
m = Prophet(holidays=holidays)
m.add_country_holidays(country_name='US')
m.fit(df)

季节性的傅立叶顺序

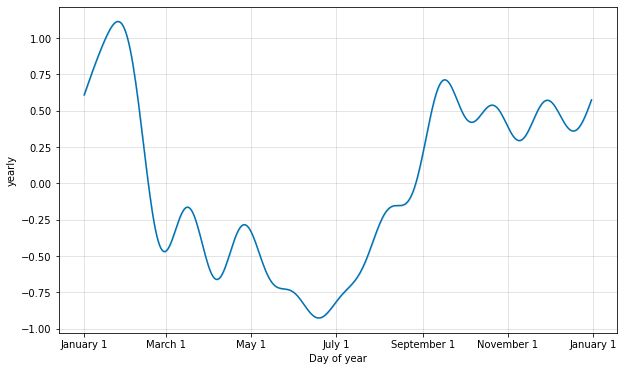
季节性是使用部分傅立叶和来估计的。有关完整详细信息，请参阅论文，以及Wikipedia上的此图，以说明部分傅立叶和如何近似任意周期信号。部分和（顺序）中的项数是一个参数，它决定了季节性变化的速度。为了说明这一点，请考虑快速入门中的 Peyton Manning 数据。年度季节性的默认傅立叶阶数是 10，它会产生这种拟合：

 

# Python
from prophet.plot import plot_yearly
m = Prophet().fit(df)
a = plot_yearly(m)

默认值通常是合适的，但是当季节性需要适应更高频率的变化时可以增加它们，并且通常不太平滑。实例化模型时，可以为每个内置季节性指定傅立叶阶数，这里增加到 20：

# Python from prophet.plot import plot_yearly m = Prophet(yearly_seasonality=20).fit(df) a = plot_yearly(m)

指定自定义季节性

如果时间序列长度超过两个周期，Prophet 将默认适合每周和每年的季节性。

可以使用add_seasonality方法 (Python) 或函数 (R)添加其他季节性（每月、每季度、每小时）。

默认情况下，Prophet 使用傅立叶阶数 3 表示每周季节性和 10 次年度季节性。一个可选的输入add_seasonality是该季节性分量的先验尺度 - 这将在下面讨论。

# Python
m = Prophet(weekly_seasonality=False)
m.add_seasonality(name='monthly', period=30.5, fourier_order=5)
forecast = m.fit(df).predict(future)
fig = m.plot_components(forecast)

取决于其他因素的季节性

# Python def is_nfl_season(ds): date = pd.to_datetime(ds) return (date.month > 8 or date.month < 2) df['on_season'] = df['ds'].apply(is_nfl_season) df['off_season'] = ~df['ds'].apply(is_nfl_season)

# Python
m = Prophet(weekly_seasonality=False)
m.add_seasonality(name='weekly_on_season', period=7, fourier_order=3, condition_name='on_season')
m.add_seasonality(name='weekly_off_season', period=7, fourier_order=3, condition_name='off_season')

future['on_season'] = future['ds'].apply(is_nfl_season)
future['off_season'] = ~future['ds'].apply(is_nfl_season)
forecast = m.fit(df).predict(future)
fig = m.plot_components(forecast)

假期和季节性的先前规模

如果您发现假期过度拟合，您可以使用参数调整它们的先验比例以平滑它们holidays_prior_scale。默认情况下，此参数为 10，它提供的正则化很少。减少此参数会抑制假期效果：

# Python
m = Prophet(holidays=holidays, holidays_prior_scale=0.05).fit(df)
forecast = m.predict(future)
forecast[(forecast['playoff'] + forecast['superbowl']).abs() > 0][
    ['ds', 'playoff', 'superbowl']][-10:]

# Python m = Prophet() m.add_seasonality( name='weekly', period=7, fourier_order=3, prior_scale=0.1)

额外的回归量

可以使用该add_regressor方法或函数将额外的回归量添加到模型的线性部分。拟合和预测数据帧中都需要存在具有回归量值的列。例如，我们可以在 NFL 赛季的周日添加额外的效果。在组件图上，此效果将显示在“extra_regressors”图中：

# Python
def nfl_sunday(ds):
    date = pd.to_datetime(ds)
    if date.weekday() == 6 and (date.month > 8 or date.month < 2):
        return 1
    else:
        return 0
df['nfl_sunday'] = df['ds'].apply(nfl_sunday)

m = Prophet()
m.add_regressor('nfl_sunday')
m.fit(df)

future['nfl_sunday'] = future['ds'].apply(nfl_sunday)

forecast = m.predict(future)
fig = m.plot_components(forecast)

乘性季节性

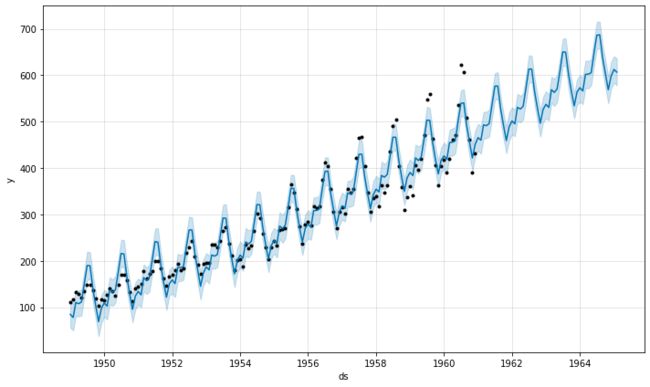
默认情况下，Prophet 拟合加性季节性，这意味着将季节性的影响添加到趋势中以获得预测。这个航空乘客数量的时间序列是加性季节性不起作用的一个例子

# Python
df = pd.read_csv('../examples/example_air_passengers.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(50, freq='MS')
forecast = m.predict(future)
fig = m.plot(forecast)

 这个时间序列有明显的年周期，但预测中的季节性在时间序列开始时太大而在末尾太小。在这个时间序列中，季节性不是 Prophet 假设的恒定附加因素，而是随趋势而增长。这是乘法季节性。

Prophet 可以通过设置seasonality_mode='multiplicative'输入参数来模拟乘法季节性：

# Python
m = Prophet(seasonality_mode='multiplicative')
m.fit(df)
forecast = m.predict(future)
fig = m.plot(forecast)

# Python
m = Prophet(seasonality_mode='multiplicative')
m.add_seasonality('quarterly', period=91.25, fourier_order=8, mode='additive')
m.add_regressor('regressor', mode='additive')

使用seasonality_mode='multiplicative'，假日效应也将被建模为乘法。默认情况下，任何添加的季节性或额外的回归量都将使用seasonality_mode设置的任何值，但可以通过在添加季节性或回归量时指定mode='additive'或mode='multiplicative'作为参数来覆盖。

例如，此块将内置季节性设置为乘法，但包括加性季度季节性和加性回归量：

不确定性区间

预测中存在三个不确定性来源：趋势的不确定性、季节性估计的不确定性和额外的观测噪声。

# Python forecast = Prophet(interval_width=0.95).fit(df).predict(future)

季节性的不确定性

默认情况下，Prophet 只会返回趋势和观察噪声的不确定性。要获得季节性的不确定性，您必须进行完整的贝叶斯抽样。这是使用参数mcmc.samples（默认为 0）完成的。我们在这里对来自 Quickstart 的 Peyton Manning 数据的前六个月执行此操作：

# Python m = Prophet(mcmc_samples=300) forecast = m.fit(df).predict(future)

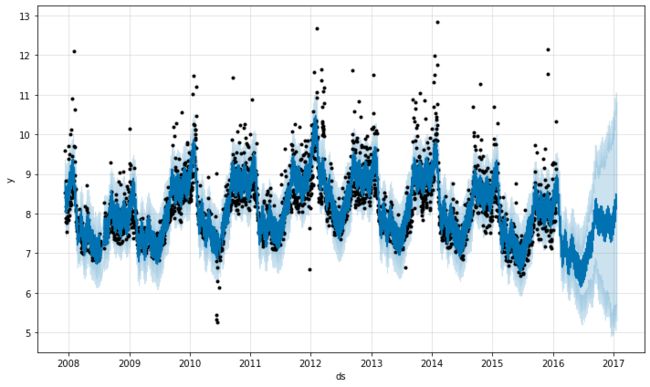
异常值

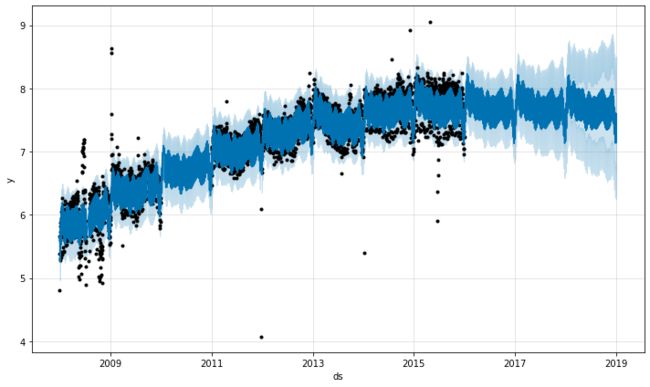
异常值影响 Prophet 预测的主要方式有两种。在这里，我们对之前记录的 Wikipedia 访问 R 页面进行了预测，但有一组错误数据：

# Python
df = pd.read_csv('../examples/example_wp_log_R_outliers1.csv')
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(periods=1096)
forecast = m.predict(future)
fig = m.plot(forecast)

 

趋势预测似乎合理，但不确定性区间似乎太宽了。Prophet 能够处理历史中的异常值，但只能通过趋势变化来拟合它们。然后，不确定性模型预计未来趋势变化幅度相似。

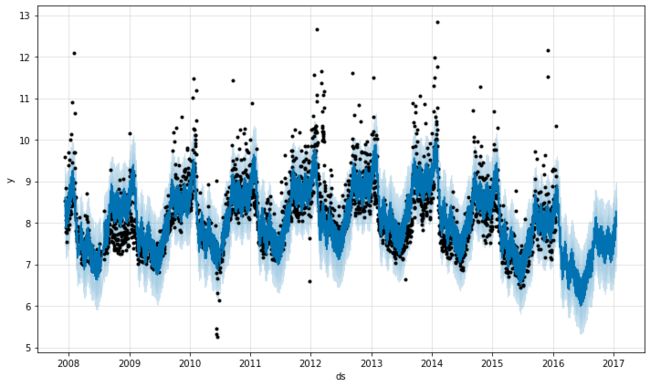
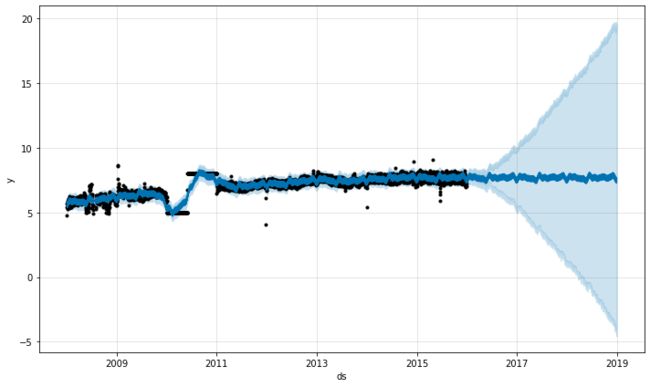
处理异常值的最佳方法是删除它们 - Prophet 没有丢失数据的问题。如果您将它们的值设置NA为历史记录但将日期保留在 中future，那么 Prophet 将为您提供对它们值的预测。

# Python
df.loc[(df['ds'] > '2010-01-01') & (df['ds'] < '2011-01-01'), 'y'] = None
model = Prophet().fit(df)
fig = model.plot(model.predict(future))

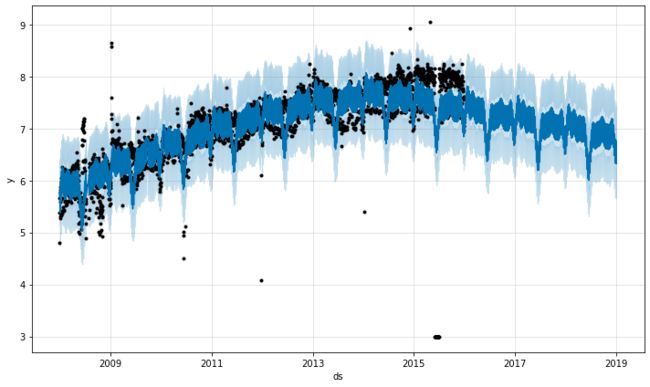
 2015 年 6 月的一组极端异常值混淆了季节性估计，因此它们的影响将永远回荡到未来。同样正确的方法是删除它们：

 

# Python
df.loc[(df['ds'] > '2015-06-01') & (df['ds'] < '2015-06-30'), 'y'] = None
m = Prophet().fit(df)
fig = m.plot(m.predict(future))

非日常数据

Prophet 可以通过在ds列中传递带有时间戳的数据帧来对具有次日观察的时间序列进行预测。时间戳的格式应为 YYYY-MM-DD HH:MM:SS - 请参阅此处的csv 示例。当使用子日数据时，将自动适应每日季节性。在这里，我们将 Prophet 拟合到具有 5 分钟分辨率的数据（优胜美地的每日温度）

# Python
df = pd.read_csv('../examples/example_yosemite_temps.csv')
m = Prophet(changepoint_prior_scale=0.01).fit(df)
future = m.make_future_dataframe(periods=300, freq='H')
fcst = m.predict(future)
fig = m.plot(fcst)

每日季节性将显示在组件图中：

# Python fig = m.plot_components(fcst)

 

有规律间隔的数据

假设上的数据集只有从 12a 到 6a 的观察：

NOTES:

可调整的参数

• changepoint_prior_scale：这可能是最有影响的参数。它决定了趋势的灵活性，特别是趋势在趋势变化点的变化程度。如本文档中所述，如果它太小，则趋势将欠拟合，并且本应使用趋势变化建模的方差最终将使用噪声项进行处理。如果它太大，趋势将过度拟合，在最极端的情况下，您最终会得到捕捉年度季节性的趋势。默认值 0.05 适用于许多时间序列，但可以调整；[0.001, 0.5] 的范围可能是正确的。像这样的参数（正则化惩罚；这实际上是套索惩罚）通常在对数尺度上进行调整。

• seasonality_prior_scale：该参数控制季节性的灵活性。同样，较大的值允许季节性适应较大的波动，较小的值会缩小季节性的幅度。默认为 10.，基本不应用正则化。那是因为我们在这里很少看到过度拟合（存在固有的正则化，因为它是用截断的傅立叶级数建模的，所以它本质上是低通滤波的）。调整它的合理范围可能是 [0.01, 10]；当设置为 0.01 时，您应该会发现季节性的幅度非常小。这在对数尺度上也可能是有意义的，因为它实际上是一个 L2 惩罚，就像在岭回归中一样。

• holidays_prior_scale：这可以控制适应假日效果的灵活性。与seasonity_prior_scale 类似，它默认为10.0，基本上不适用正则化，因为我们通常对假期有多个观察，并且可以很好地估计它们的影响。这也可以在 [0.01, 10] 的范围内进行调整，就像与seasonality_prior_scale 一样。

• seasonality_mode: 选项是 [ 'additive', 'multiplicative']。默认为'additive'，但许多业务时间序列将具有乘法季节性。最好仅通过查看时间序列并查看季节性波动的幅度是否随着时间序列的幅度而增长（请参阅此处有关乘法季节性的文档）来确定这一点，但如果不可能，则可以对其进行调整。

也许调？

• changepoint_range：这是允许趋势变化的历史比例。这默认为 0.8，即历史的 80%，这意味着模型将不适合时间序列最后 20% 的任何趋势变化。这是相当保守的，以避免在时间序列的最后没有足够的跑道来适应趋势变化而过度拟合。有了人在循环中，这可以很容易地从视觉上识别出来：人们可以很清楚地看到预测在最后 20% 中是否做得不好。在全自动设置中，不那么保守可能是有益的。如上所述，可能无法通过交叉验证有效地调整此参数。模型从时间序列的最后 10% 的趋势变化中概括的能力将很难通过查看在最后 10% 中可能没有趋势变化的早期截止点来学习。所以，这个参数最好不要调整，除非可能是在大量时间序列上。在这种情况下，[0.8, 0.95] 可能是一个合理的范围。

可能不会调整的参数

• growth：选项是“线性”和“后勤”。这可能不会被调整；如果有一个已知的饱和点并且向该点增长，它将被包括在内并使用逻辑趋势，否则它将是线性的。

• changepoints：这是用于手动指定更改点的位置。默认情况下没有，它会自动放置它们。

• n_changepoints：这是自动放置的变更点的数量。默认值 25 应该足以捕捉典型时间序列中的趋势变化（至少 Prophet 无论如何都能很好地处理的类型）。与其增加或减少变更点的数量，不如专注于增加或减少这些趋势变化的灵活性，这是通过changepoint_prior_scale.

• yearly_seasonality: 默认情况下 ('auto') 如果有一年的数据，这将打开年度季节性，否则关闭。选项是 ['auto', True, False]。如果有超过一年的数据，与其在 HPO 期间尝试将其关闭，不如将其保持打开状态并通过调整来降低季节性影响seasonality_prior_scale。

• weekly_seasonality: 和 一样yearly_seasonality。

• daily_seasonality: 和 一样yearly_seasonality。

• holidays: 这是传入指定假期的数据框。假期效果将与holidays_prior_scale.

• mcmc_samples：是否使用 MCMC 可能取决于时间序列的长度和参数不确定性的重要性等因素（这些注意事项在文档中进行了描述）。

• interval_width：Prophetpredict返回每个组件的不确定性区间，例如yhat_lower和yhat_upper预测yhat。这些计算为后验预测分布的interval_width分位数，并指定要使用的分位数。默认值 0.8 提供 80% 的预测区间。如果您想要 95% 的间隔，您可以将其更改为 0.95。这只会影响不确定性区间，根本不会改变预测yhat，因此不需要调整。

• uncertainty_samples：不确定性区间计算为后验预测区间的分位数，后验预测区间使用蒙特卡罗采样估计。此参数是要使用的样本数（默认为 1000）。predict 的运行时间在这个数字上是线性的。减小它会增加不确定性区间的方差（蒙特卡罗误差），增大它会减小该方差。因此，如果不确定性估计看起来参差不齐，则可以增加以进一步平滑它们，但可能不需要更改。同样interval_width，这个参数只影响不确定性区间，改变它不会以任何方式影响预测yhat；它不需要调整。

• stan_backend: 如果pystan和cmdstanpy后端都设置了，可以指定后端。预测将是相同的，这不会被调整。

在 Python 中，不应使用 pickle 保存模型；附加到模型对象的 Stan 后端不会很好地进行腌制，并且会在某些 Python 版本下产生问题。相反，您应该使用内置的序列化函数将模型序列化为 json：

# Python
import json
from prophet.serialize import model_to_json, model_from_json

with open('serialized_model.json', 'w') as fout:
    json.dump(model_to_json(m), fout)  # Save model

with open('serialized_model.json', 'r') as fin:
    m = model_from_json(json.load(fin))  # Load model