Atcoder ABC232-E Rook Path

Atcoder ABC232-E Rook Path

题目大意

有一个$H\ast W$的表格， 在表格中有个车， 它开始在$(x_1,y_1)$的位置，它可以移动到同一个行或同一列的其他格子，但不能原地不动。 现在，请问移动$K$次，它恰好出现在$(x_2,y_2)$的方案数。 答案可能很大，你需要$(mod998244353)$

思路

比赛看题表忙忙，赛后题解脑茫茫，直到上问Depseaspary才取得真经。

这题还是老熟人dp

转移方程

我们设$f[i][j][k]$表示 移动$k$次到达 第$i$行 第$j$列 的方案数，于是很容易想到$k-1$的第$i$行加上的$j$行的和减去2倍（加行算一次，加列算一次）自己（不可以停留不动）,即：

$$f[i][j][k]=\sum _{i=1}^{H}f[i][j][k-1]+\sum _{j=1}^{W}f[i][j][k-1]-2\ast f[i][j][k-1]$$
我们再设$h[i][k]$为 第$k$次移动到达第$i$行的方案数的和 ，$w[j][k]$为 第$k$次移动到达第$j$列的方案数的和。
$$f[i][j][k]=h[i][k-1]+w[j][k-1]-2\ast f[i][j][k-1]$$

设$A[k]$ IOI 表示步数为$k$时的表格中方案数的和。

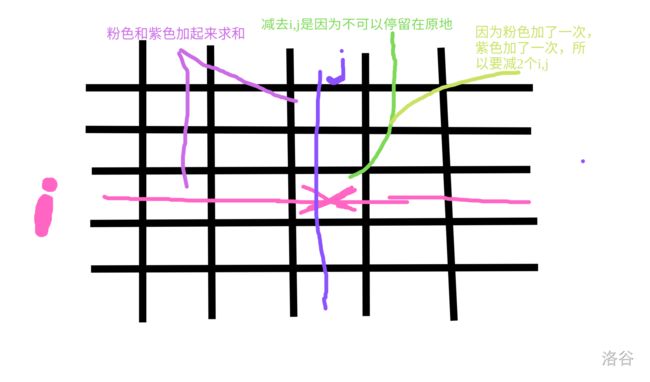
如图：

• 第$i$行的每一个格子$(i,j)$（$i$是固定的，$j$会变动）的方案数都为$h[i][k-1]$加$w[j][k-1]$，图中的紫线加上所在列的蓝线的和。
• 由于$j$有$W$个位置可以取，而${\sum }_{j=1}^{W}w[j][k-1]$就是整个表格在$k-1$步时的方案数的和，即$A[k-1]$。
• 由于$j$有$W$个位置可以取，所以$h[i][k-1]$会被加$W$次，即$h[i][k-1]\ast W$.
• 因为不可以不走动，所以应该减去停留不动的情况。又$i$行被加两次（$A[k-1]$ 和 每一个$i$行格子自己相加（$=h[i][k-1]$））即$2\ast h[i][k-1]$

$$h[i][k]=h[i][k-1]\ast W+A[k-1]-2\ast h[i][k-1]=(W-2)\ast h[i][k-1]+A[k-1]$$

$w[j][k]$也可以如上推理表示。
$$w[j][k]=w[j][k-1]\ast H+A[k-1]-2\ast W[j][k-1]=(H-2)\ast w[j][k-1]+A[k-1]$$

现在我们发现只有$A[k]$这个小淘气还没有被宝表示出来，那我们也给$A[k]$量身定制一套表示方案

对与$A[k]$中每一个点$(i,j)$，都是由其$k-1$步时的行加列所得，那么每一行会被加$W$次，每一列会被加$H$次，那么每一个点就会加$H+W$次 。

那么$A[k]=A[k-1]\ast (H+W)$

因为不可以走动的老规则，所以答案应该$-2$。
$$A[k]=A[k-1]\ast (H+W-2)$$

状态转移方程总结

当第$k$步时

$(i,j)$方案数
$$f[i][j][k]=h[i][k-1]+w[j][k-1]-2\ast f[i][j][k-1]$$
$i$行的方案数
$$h[i][k]=(W-2)\ast h[i][k-1]+A[k-1]$$
$j$列的方案数
$$w[j][k]=(H-2)\ast w[j][k-1]+A[k-1]$$
全图总方案数
$$A[k]=A[k-1]\ast (H+W-2)$$

初始值

$A[0]=1$

第0步时，只有$(x1,y1)$出生点可以到达

如果$x1==x2$ 那么$h[x1][0]=1$

$x1(x2)$行在没走的时候就可以到达

如果$y1==y2$ 那么$w[y1][0]=1$

$y1(y2)$列在没走的时候就可以到达

优化

如果你看数据范围的话，你会有手撕出题人的想法……

难不成我们手推这么久的光阴就要浪费了吗？

为让Depseaspary开心点老实点，我们先观察方程。

不难发现，方程中的行号和列号根本没变！

也就是说，我们没必要去开行和列的数组，更不用枚举行和列，直接求和不就完了！

CODE

#include
using namespace std;

#define ll long long

const int maxn=2e6+5,mod=998244353;

ll n,m,k,sx,sy,ex,ey;
ll f[maxn],h[maxn],w[maxn],a[maxn];

int main()
{
    scanf("%lld%lld%lld%lld%lld%lld%lld",&n,&m,&k,&sx,&sy,&ex,&ey);
    a[0]=1;
    for(int i=1;i<=k;i++) a[i]=(a[i-1]*((n+m-2)%mod))%mod;

    if(sx==ex) h[0]=1;
    if(sy==ey) w[0]=1;
    if(sx==ex&&sy==ey) f[0]=1;
    for(int i=1;i<=k;i++) h[i]=((h[i-1]*((m-2)%mod))%mod+a[i-1])%mod;
    for(int i=1;i<=k;i++) w[i]=((w[i-1]*((n-2)%mod))%mod+a[i-1])%mod;

    for(int i=1;i<=k;i++) f[i]=(((h[i-1]+w[i-1])%mod)-(2*f[i-1]%mod))%mod;

    printf("%lld",(f[k]+mod)%mod);//防止负数
}

在最后的最后，我愿意说一句：“Depseaspary Orz”。