【PyTorch基础教程21】进阶训练技巧（损失函数、学习率、模型微调、半精度训练）

学习总结

• 自定义损失函数：函数定义、类定义（用得更多）。注意涉及到数学运算时，我们最好全程使用PyTorch提供的张量计算接口，这样就不需要我们实现自动求导功能并且我们可以直接调用cuda。
• 动态调整学习率：pytorch内置scheduler或者自定义scheduler。
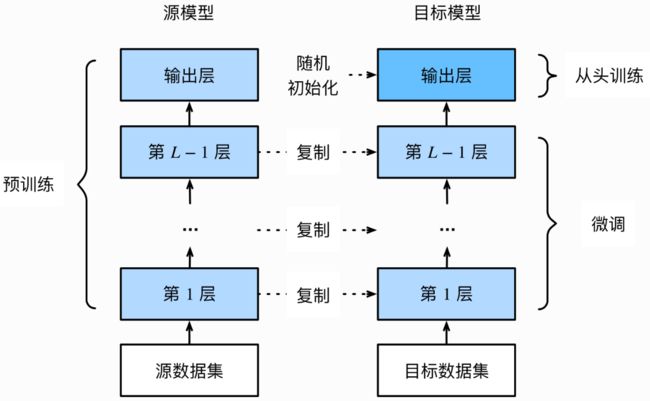
• 模型微调：迁移学习的应用场景，如在目标数据集上训练目标模型，将从头训练输出层，而其余层的参数都是基于源模型的参数微调得到的。
  • 获取pytorch中的预训练模型，冻结预训练模型中所有参数；
  • 然后模型微调：如替换ResNet最后的2层网络，返回一个新模型
• 半精度训练：PyTorch默认的浮点数存储方式用的是torch.float32，小数点后位数更多固然能保证数据的精确性，但绝大多数场景其实并不需要这么精确，只保留一半的信息也不会影响结果，也就是使用torch.float16格式。

一、自定义损失函数

PyTorch在torch.nn模块为我们提供了许多常用的损失函数，比如：MSELoss，L1Loss，BCELoss等，但是有些时候我们需要自定义损失函数，提升模型的表现，如DiceLoss，HuberLoss，SobolevLoss等都没在pytorch库中。

1.1 以函数方式定义

自定义损失函数：

def my_loss(output, target):
    loss = torch.mean((output - target)**2)
    return loss

1.2 以类方式定义

• 虽然以函数定义的方式很简单，但是以类方式定义更加常用，在以类方式定义损失函数时，我们如果看每一个损失函数的继承关系我们就可以发现Loss函数部分继承自_loss, 部分继承自_WeightedLoss, 而_WeightedLoss继承自_loss，_loss继承自 nn.Module。
• 在自定义损失函数时，涉及到数学运算时，最好全程使用PyTorch提供的张量计算接口，这样就不需要我们实现自动求导功能并且我们可以直接调用cuda，使用numpy或者scipy的数学运算时，操作会有些麻烦。
• 关于PyTorch使用Class定义损失函数的原因，可以参考PyTorch的讨论区（链接6）

我们可以将其当作神经网络的一层来对待，同样地，我们的损失函数类就需要继承自nn.Module类。Dice Loss是一种在分割领域常见的损失函数，定义如下：

$$DSC=\frac{2|X\cap Y|}{|X|+|Y|}$$
实现代码如下：

class DiceLoss(nn.Module):
    def __init__(self,weight=None,size_average=True):
        super(DiceLoss,self).__init__()
        
	def forward(self,inputs,targets,smooth=1):
        inputs = F.sigmoid(inputs)       
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        intersection = (inputs * targets).sum()                   
        dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)  
        return 1 - dice

# 使用方法    
criterion = DiceLoss()
loss = criterion(input,targets)

除此之外，常见的损失函数还有BCE-Dice Loss，Jaccard/Intersection over Union (IoU) Loss，Focal Loss…

class DiceBCELoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(DiceBCELoss, self).__init__()

    def forward(self, inputs, targets, smooth=1):
        inputs = F.sigmoid(inputs)       
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        intersection = (inputs * targets).sum()                     
        dice_loss = 1 - (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)  
        BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
        Dice_BCE = BCE + dice_loss
        
        return Dice_BCE
--------------------------------------------------------------------
    
class IoULoss(nn.Module):
    def __init__(self, weight=None, size_average=True):
        super(IoULoss, self).__init__()

    def forward(self, inputs, targets, smooth=1):
        inputs = F.sigmoid(inputs)       
        inputs = inputs.view(-1)
        targets = targets.view(-1)
        intersection = (inputs * targets).sum()
        total = (inputs + targets).sum()
        union = total - intersection 
        
        IoU = (intersection + smooth)/(union + smooth)
                
        return 1 - IoU

# 更多的可以参考链接1

1.3 用自定义损失函数的完整栗子

下面以训练简单模型（线性回顾）为栗子，使用自定义的损失函数。

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt


#自定义损失函数

# 1. 继承nn.Mdule
class My_loss(nn.Module):
    def __init__(self):
        super().__init__()
        
    def forward(self, x, y):
        return torch.mean(torch.pow((x - y), 2))


# 2. 直接定义函数 ， 不需要维护参数，梯度等信息
# 注意所有的数学操作需要使用tensor完成。
def my_mse_loss(x, y):
    return torch.mean(torch.pow((x - y), 2))

# 3, 如果使用 numpy/scipy的操作  可能使用nn.autograd.function来计算了
# 要实现forward和backward函数

# Hyper-parameters 定义迭代次数， 学习率以及模型形状的超参数
input_size = 1
output_size = 1
num_epochs = 60
learning_rate = 0.001

# Toy dataset  1. 准备数据集
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168], 
                    [9.779], [6.182], [7.59], [2.167], [7.042], 
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573], 
                    [3.366], [2.596], [2.53], [1.221], [2.827], 
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)

# Linear regression model  
# 2. 定义网络结构 y=w*x+b 其中w的size [1,1], b的size[1,]
model = nn.Linear(input_size, output_size)

# Loss and optimizer 3.定义损失函数， 使用的是最小平方误差函数
# criterion = nn.MSELoss()
# 自定义函数1
criterion = My_loss()

# 4.定义迭代优化算法， 使用的是随机梯度下降算法
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)  
loss_dict = []
# Train the model 5. 迭代训练
for epoch in range(num_epochs):
    # Convert numpy arrays to torch tensors  5.1 准备tensor的训练数据和标签
    inputs = torch.from_numpy(x_train)
    targets = torch.from_numpy(y_train)

    # Forward pass  5.2 前向传播计算网络结构的输出结果
    outputs = model(inputs)
    # 5.3 计算损失函数
    # loss = criterion(outputs, targets)
    
    # 1. 自定义函数1
    # loss = criterion(outputs, targets)
    # 2. 自定义函数
    loss = my_mse_loss(outputs, targets)
    # Backward and optimize 5.4 反向传播更新参数
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    
    # 可选 5.5 打印训练信息和保存loss
    loss_dict.append(loss.item())
    if (epoch+1) % 5 == 0:
        print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

# Plot the graph 画出原y与x的曲线与网络结构拟合后的曲线
predicted = model(torch.from_numpy(x_train)).detach().numpy()
plt.plot(x_train, y_train, 'ro', label='Original data')
plt.plot(x_train, predicted, label='Fitted line')
plt.legend()
plt.show()

# 画loss在迭代过程中的变化情况
plt.plot(loss_dict, label='loss for every epoch')
plt.legend()
plt.show()

结果为：

Epoch [5/60], Loss: 13.8641
Epoch [10/60], Loss: 5.9160
Epoch [15/60], Loss: 2.6956
Epoch [20/60], Loss: 1.3905
Epoch [25/60], Loss: 0.8613
Epoch [30/60], Loss: 0.6463
Epoch [35/60], Loss: 0.5588
Epoch [40/60], Loss: 0.5228
Epoch [45/60], Loss: 0.5077
Epoch [50/60], Loss: 0.5011
Epoch [55/60], Loss: 0.4979
Epoch [60/60], Loss: 0.4961

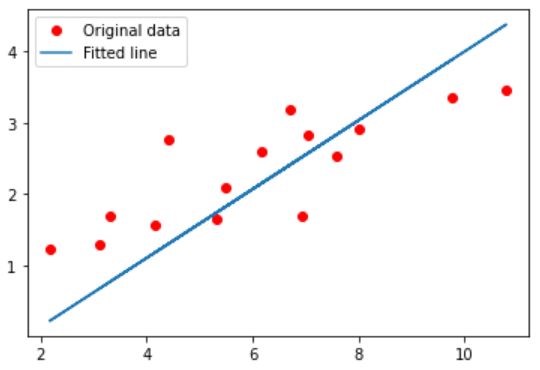
画出原y与x的数据，网络结构拟合后的曲线：

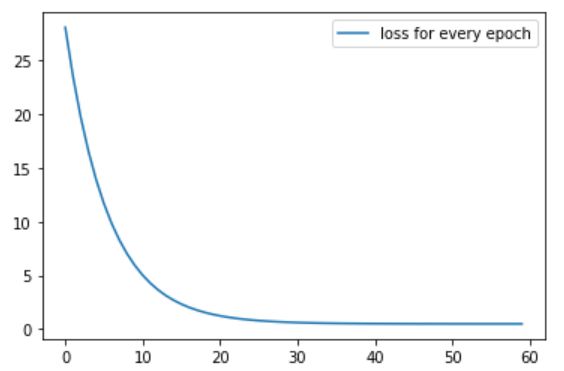
画loss在迭代过程中的变化情况：

二、动态调整学习率

• 学习率的选择是深度学习中一个困扰人们许久的问题，学习速率设置过小，会极大降低收敛速度，增加训练时间；学习率太大，可能导致参数在最优解两侧来回振荡。
• 但是当我们选定了一个合适的学习率后，经过许多轮的训练后，可能会出现准确率震荡或loss不再下降等情况，说明当前学习率已不能满足模型调优的需求。可以使用scheduler机制：选择一个适当的学习率衰减策略来改善这种现象，提高我们的精度。

2.1 使用官方scheduler

（1）官方scheduler的API

在训练神经网络的过程中，学习率是最重要的超参数之一，PyTorch已经在torch.optim.lr_scheduler封装好了一些动态调整学习率的方法供我们使用，列出部分scheduler。

• lr_scheduler.LambdaLR
• lr_scheduler.MultiplicativeLR
• lr_scheduler.StepLR
• lr_scheduler.MultiStepLR
• lr_scheduler.ExponentialLR
• lr_scheduler.CosineAnnealingLR

# 选择一种优化器
optimizer = torch.optim.Adam(...) 
# 选择上面提到的一种或多种动态调整学习率的方法
scheduler1 = torch.optim.lr_scheduler.... 
scheduler2 = torch.optim.lr_scheduler....
...
schedulern = torch.optim.lr_scheduler....
# 进行训练
for epoch in range(100):
    train(...)
    validate(...)
    optimizer.step()
    # 需要在优化器参数更新之后再动态调整学习率
	scheduler1.step() 
	...
    schedulern.step()

（2）使用scheduler的栗子

• 使用官方给出的torch.optim.lr_scheduler时，需要将scheduler.step()放在optimizer.step()后面进行使用。
• 下面以torch.optim.lr_scheduler.LambdaLR为栗，其更新策略为：new_lr $=\lambda \times$ initial_lr，其中new_lr是得到的新的学习率，initial_lr是初始的学习率，$\lambda$是通过参数lr_lambda和epoch得到的。

class torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)

• torch.optim.lr_scheduler.LambdaLR的参数：
  • optimizer （Optimizer）：要更改学习率的优化器；
  • lr_lambda（function or list）：根据epoch计算$\lambda$的函数；或者是一个list的这样的function，分别计算各个parameter groups的学习率更新用到的$\lambda$；
  • last_epoch （int）：最后一个epoch的index，如果是训练了很多个epoch后中断了，继续训练，这个值就等于加载的模型的epoch。默认为-1表示从头开始训练，即从epoch=1开始。
• 下面栗子只是看每个epoch对应的学习速率，更新网络参数时省略了loss.backward()。

import torch
import torch.nn as nn
from torch.optim.lr_scheduler import LambdaLR

initial_lr = 0.1

class model(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=3)

    def forward(self, x):
        pass

net_1 = model()

optimizer_1 = torch.optim.Adam(net_1.parameters(), lr = initial_lr)
scheduler_1 = LambdaLR(optimizer_1, lr_lambda=lambda epoch: 1/(epoch+1))

print("初始化的学习率：", optimizer_1.defaults['lr'])

for epoch in range(1, 11):
    # train

    optimizer_1.zero_grad()
    optimizer_1.step()
    print("第%d个epoch的学习率：%f" % (epoch, optimizer_1.param_groups[0]['lr']))
    scheduler_1.step()

############  结果如下   #################
初始化的学习率： 0.1
第1个epoch的学习率：0.100000
第2个epoch的学习率：0.050000
第3个epoch的学习率：0.033333
第4个epoch的学习率：0.025000
第5个epoch的学习率：0.020000
第6个epoch的学习率：0.016667
第7个epoch的学习率：0.014286
第8个epoch的学习率：0.012500
第9个epoch的学习率：0.011111
第10个epoch的学习率：0.010000

2.2 自定义scheduler

在实验中也有可能碰到需要我们自己定义学习率调整策略的情况，可以自定义函数adjust_learning_rate来改变param_group中lr的值。

假设现在实验中，需要学习率每30轮下降为原来的1/10，假设已有的官方API中没有符合我们需求的，那就需要自定义函数来实现学习率的改变。

def adjust_learning_rate(optimizer, epoch):
    lr = args.lr * (0.1 ** (epoch // 30))
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr

有了adjust_learning_rate函数的定义，在训练的过程就可以调用我们的函数来实现学习率的动态变化。

def adjust_learning_rate(optimizer,...):
    ...
optimizer = torch.optim.SGD(model.parameters(),lr = args.lr,momentum = 0.9)
for epoch in range(10):
    train(...)
    validate(...)
    adjust_learning_rate(optimizer,epoch)

三、模型微调

• 随着深度学习的发展，模型的参数越来越大，许多开源模型都是在较大数据集上进行训练的，比如Imagenet-1k，Imagenet-11k，甚至是ImageNet-21k等。但在实际应用中，我们的数据集可能只有几千张，这时从头开始训练具有几千万参数的大型神经网络是不现实的，因为越大的模型对数据量的要求越大，过拟合无法避免。

• 场景：现在想从图像中识别出不同种类的椅子，然后将购买链接推荐给用户。

• 方法：先找出100种常见的椅子，为每种椅子拍摄1000张不同角度的图像，然后在收集到的图像数据集上训练一个分类模型。这个椅子数据集，样本数仍然不及ImageNet数据集中样本数的十分之⼀。这可能会导致使用于ImageNet数据集的复杂模型在这个椅子数据集上过拟合。同时，因为数据量有限，最终训练得到的模型的精度也可能达不到实用的要求。

  • 解决方法1：收集更多数据，耗时耗力耗钱。
  • 解决办法2：应用迁移学习(transfer learning)，将从源数据集学到的知识迁移到目标数据集上。迁移学习的一大应用场景是模型微调（finetune）。简单来说，就是我们先找到一个同类的别人训练好的模型，把别人现成的训练好了的模型拿过来，换成自己的数据，通过训练调整一下参数。

例如，虽然ImageNet数据集的图像大多跟椅子无关，但在该数据集上训练的模型可以抽取较通用的图像特征，从而能够帮助识别边缘、纹理、形状和物体组成等。这些类似的特征对于识别椅子也可能同样有效。

在PyTorch中提供了许多预训练好的网络模型（VGG，ResNet系列，mobilenet系列…），这些模型都是PyTorch官方在相应的大型数据集训练好的。学习如何进行模型微调，可以方便我们快速使用预训练模型完成自己的任务。

3.1 模型微调的流程

• 在源数据集(如ImageNet数据集)上预训练一个神经网络模型，即源模型。
• 创建一个新的神经网络模型，即目标模型。它复制了源模型上除了输出层外的所有模型设计及其参数。
  • 我们假设这些模型参数包含了源数据集上学习到的知识，且这些知识同样适用于目标数据集。
  • 我们还假设源模型的输出层跟源数据集的标签紧密相关，因此在目标模型中不予采用。
• 为目标模型添加一个输出大小为目标数据集类别个数的输出层，并随机初始化该层的模型参数。
• 在目标数据集上训练目标模型。我们将从头训练输出层，而其余层的参数都是基于源模型的参数微调得到的。

3.2 使用pytorch已有模型

这里我们以torchvision中的常见模型为例，列出了如何在图像分类任务中使用PyTorch提供的常见模型结构和参数。对于其他任务和网络结构，使用方式是类似的：

• 实例化网络

import torchvision.models as models
resnet18 = models.resnet18()
# resnet18 = models.resnet18(pretrained=False)  等价于与上面的表达式
alexnet = models.alexnet()
vgg16 = models.vgg16()
squeezenet = models.squeezenet1_0()
densenet = models.densenet161()
inception = models.inception_v3()
googlenet = models.googlenet()
shufflenet = models.shufflenet_v2_x1_0()
mobilenet_v2 = models.mobilenet_v2()
mobilenet_v3_large = models.mobilenet_v3_large()
mobilenet_v3_small = models.mobilenet_v3_small()
resnext50_32x4d = models.resnext50_32x4d()
wide_resnet50_2 = models.wide_resnet50_2()
mnasnet = models.mnasnet1_0()

• 传递pretrained参数

通过True或者False来决定是否使用预训练好的权重，在默认状态下pretrained = False，意味着我们不使用预训练得到的权重，当pretrained = True，意味着我们将使用在一些数据集上预训练得到的权重。

import torchvision.models as models
resnet18 = models.resnet18(pretrained=True)
alexnet = models.alexnet(pretrained=True)
squeezenet = models.squeezenet1_0(pretrained=True)
vgg16 = models.vgg16(pretrained=True)
densenet = models.densenet161(pretrained=True)
inception = models.inception_v3(pretrained=True)
googlenet = models.googlenet(pretrained=True)
shufflenet = models.shufflenet_v2_x1_0(pretrained=True)
mobilenet_v2 = models.mobilenet_v2(pretrained=True)
mobilenet_v3_large = models.mobilenet_v3_large(pretrained=True)
mobilenet_v3_small = models.mobilenet_v3_small(pretrained=True)
resnext50_32x4d = models.resnext50_32x4d(pretrained=True)
wide_resnet50_2 = models.wide_resnet50_2(pretrained=True)
mnasnet = models.mnasnet1_0(pretrained=True)

注意事项：

1. 通常PyTorch模型的扩展为.pt或.pth，程序运行时会首先检查默认路径中是否有已经下载的模型权重，一旦权重被下载，下次加载就不需要下载了。

2. 一般情况下预训练模型的下载会比较慢，我们可以直接通过迅雷或者其他方式去 这里 查看自己的模型里面model_urls，然后手动下载，预训练模型的权重在Linux和Mac的默认下载路径是用户根目录下的.cache文件夹。在Windows下就是C:\Users\\.cache\torch\hub\checkpoint。我们可以通过使用 torch.utils.model_zoo.load_url()设置权重的下载地址。

3. 如果觉得麻烦，还可以将自己的权重下载下来放到同文件夹下，然后再将参数加载网络。

   self.model = models.resnet50(pretrained=False)
   self.model.load_state_dict(torch.load('./model/resnet50-19c8e357.pth'))
   

4. 如果中途强行停止下载的话，一定要去对应路径下将权重文件删除干净，要不然可能会报错。

3.3 如何指定训练模型的部分层

在默认情况下，参数的属性.requires_grad = True，如果我们从头开始训练或微调不需要注意这里。但如果我们正在提取特征并且只想为新初始化的层计算梯度，其他参数不进行改变。那我们就需要通过设置requires_grad = False来冻结部分层。在PyTorch官方中提供了这样一个例程。

def set_parameter_requires_grad(model, feature_extracting):
    if feature_extracting:
        for param in model.parameters():
            param.requires_grad = False

• 在下面我们仍旧使用resnet18为例的将1000类改为4类，但是仅改变最后一层的模型参数，不改变特征提取的模型参数；
  • 注意我们先冻结模型参数的梯度；
  • 再对模型输出部分的全连接层进行修改，这样修改后的全连接层的参数就是可计算梯度的。
• 之后在训练过程中，model仍会进行梯度回传，但是参数更新则只会发生在fc层。通过设定参数的requires_grad属性，我们完成了指定训练模型的特定层的目标，这对实现模型微调非常重要。

import torchvision.models as models
# 冻结参数的梯度
feature_extract = True
model = models.resnet18(pretrained=True)
set_parameter_requires_grad(model, feature_extract)
# 修改模型
num_ftrs = model.fc.in_features
model.fc = nn.Linear(in_features=512, out_features=4, bias=True)

这里举个Pytorch肺部感染识别中的模型微调栗子（完整过程见下一篇—【Pytorch基础教程22】肺部感染识别任务（模型微调实战）），我们直接拿torchvision.models.resnet50模型微调，首先冻结预训练模型中的所有参数，然后替换掉最后两层的网络（替换2层池化层，还有fc层改为dropout，正则，线性，激活等部分），最后返回模型：

# 8 更改池化层
class AdaptiveConcatPool2d(nn.Module):
    def __init__(self, size=None):
        super().__init__()
        size = size or (1, 1) # 池化层的卷积核大小，默认值为（1，1）
        self.pool_one = nn.AdaptiveAvgPool2d(size) # 池化层1
        self.pool_two = nn.AdaptiveAvgPool2d(size) # 池化层2

    def forward(self, x):
        return torch.cat([self.pool_one(x), self.pool_two(x), 1]) # 连接两个池化层


# 7 迁移学习：拿到一个成熟的模型，进行模型微调
def get_model():
    model_pre = models.resnet50(pretrained=True) # 获取预训练模型
    # 冻结预训练模型中所有的参数
    for param in model_pre.parameters():
        param.requires_grad = False
    # 微调模型：替换ResNet最后的两层网络，返回一个新的模型
    model_pre.avgpool = AdaptiveConcatPool2d() # 池化层替换
    model_pre.fc = nn.Sequential(
        nn.Flatten(), # 所有维度拉平
        nn.BatchNorm1d(4096), # 256 x 6 x 6   ——> 4096
        nn.Dropout(0.5),  # 丢掉一些神经元
        nn.Linear(4096, 512),  # 线性层的处理
        nn.ReLU(), # 激活层
        nn.BatchNorm1d(512), # 正则化处理
        nn.Linear(512,2),
        nn.LogSoftmax(dim=1), # 损失函数
    )

    return model_pre

四、半精度训练

Pytorch模型经常需要用到硬件GPU加速，GPU的性能主要分为两部分：

• 算力：前者决定了显卡计算的速度
• 显存：后者则决定了显卡可以同时放入多少数据用于计算。

在可以使用的显存数量一定的情况下，每次训练能够加载的数据更多（也就是batch size更大），则也可以提高训练效率。

显存很重要：有时候数据本身也比较大（比如3D图像、视频等），显存较小的情况下可能甚至batch size为1的情况都无法实现。

我们观察PyTorch默认的浮点数存储方式用的是torch.float32，小数点后位数更多固然能保证数据的精确性，但绝大多数场景其实并不需要这么精确，只保留一半的信息也不会影响结果，也就是使用torch.float16格式。由于数位减了一半，因此被称为“半精度”。

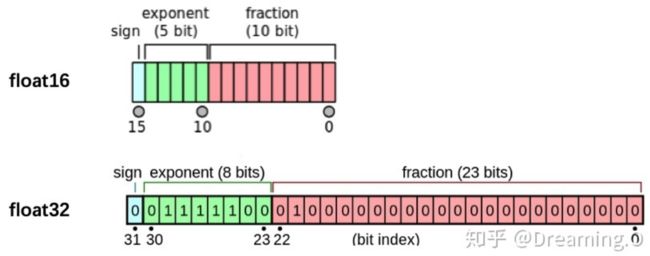
显然半精度能够减少显存占用，使得显卡可以同时加载更多数据进行计算。

4.1 半精度训练的设置

在PyTorch中使用autocast配置半精度训练，同时需要在下面三处加以设置：

• import autocast

from torch.cuda.amp import autocast

• 模型设置

在模型定义中，使用python的装饰器方法，用autocast装饰模型中的forward函数。关于装饰器的使用，可以参考这里：

@autocast()   
def forward(self, x):
    ...
    return x

• 训练过程

在训练过程中，只需在将数据输入模型及其之后的部分放入“with autocast():“即可：

 for x in train_loader:
	x = x.cuda()
	with autocast():
        output = model(x)
        ...

4.2 使用半精度训练的注意事项

半精度训练主要适用于数据本身的size比较大（比如说3D图像、视频等）。当数据本身的size并不大时（比如手写数字MNIST数据集的图片尺寸只有28*28），使用半精度训练则可能不会带来显著的提升。

Reference

1. https://www.kaggle.com/bigironsphere/loss-function-library-keras-pytorch/notebook
2. https://www.zhihu.com/question/66988664/answer/247952270
3. https://blog.csdn.net/dss_dssssd/article/details/84103834
4. 图像处理：自定义损失函数
5. pytorch教程之损失函数详解——多种定义损失函数的方法
6. https://discuss.pytorch.org/t/should-i-define-my-custom-loss-function-as-a-class/89468
7. datawhale notebook
8. PyTorch官方文档：https://pytorch.org/docs/stable/optim.html
9. 参数更新
10. 给不同层分配不同的学习率
11. torch.optim.lr_scheduler：调整学习率
12. PyTorch 1.0 中文官方教程：Torchvision模型微调
13. 动手学深度学习(pytorch)-21 模型微调