机器学习（三）Logistic回归
Logistic回归
- 1.Logistic回归概述
-
- 1.1Logistic回归的一般过程：
- 2.基于 Logistic 回归和 Sigmoid 函数的分类
-
- 2.1 Sigmoid函数
- 3. 基于最优化方法的最佳回归系数确定
-
- 3.1 梯度上升法
- 4. 代码实现
-
- 4.1 数据集可视化
- 4.2 使用梯度上升找到最佳参数
- 4.3 画出决策边界
- 4.4 随机梯度上升算法
- 4.5 回归系数与迭代次数的关系
- 5. 从疝气病症预测病马死亡率
-
- 5.1 准备数据
- 5.2 测试算法：用Logistic 回归进行分类
- 6. 实验小结
1.Logistic回归概述
假设现在有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“回归”一词源于最佳拟合，表示要找到最佳拟合参数集。
训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。
1.1Logistic回归的一般过程：
2.基于 Logistic 回归和 Sigmoid 函数的分类
2.1 Sigmoid函数
对于给定的一些数据集，我们想要得到一个函数，它能够接受所有的输入然后预测出类别。例如在两个类的情况下，函数输出0或1，该函数称为海维塞德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。但是海维塞德阶跃函数的问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。不过另外一个函数也有类似的性质，而且数学上更容易处理，它就是Sigmoid函数，具体公式如下：
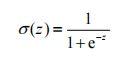
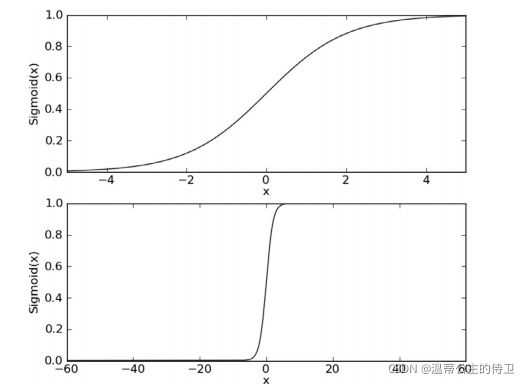
如下面两张图所示，这是Sigmoid函数在不同坐标尺度下的两条曲线图。当x为0时，Sigmoid函数值为0.5。
随着x的增大，对应的Sigmoid值将逼近于1；而随着x的减小，Sigmoid值将逼近于0。如果横坐标
刻度足够大（图5-1下图），Sigmoid函数看起来很像一个阶跃函数。
为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。
3. 基于最优化方法的最佳回归系数确定
Sigmoid函数的输入记为z，由下面公式得出：
如果采用向量的写法，上述公式可以写成
它表示将这两个数值向量对应元素相乘然后全部加起来即得到z值。其中的向量x是分类器的输入数据，向量w也就是我们要找到的最佳参数（系数），从而使得分类器尽可能地精确。为了寻找该最佳参数，需要用到最优化理论的一些知识。
3.1 梯度上升法
梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为∇，则函数f(x,y)的梯度由下式表示：
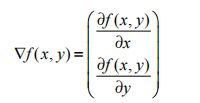
这个梯度意味着要沿x的方向移动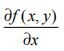
，沿y的方向移动
。其中，函数f (x,y)必须要在待计算的点上有定义并且可微。
一个具体的函数例子见图：
梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始，计算完该点的梯度，函数就根据梯度移动到下一点P1。在P1点，梯度再次被重新计算，并沿新的梯度方向移动到P2。如此循环迭代，直到满足停止条件。迭代的过程中，梯度算子总是保证我们能选取到最佳的移动方向。
可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记做α。用向量来表示的话，梯度上升算法的迭代公式如下：
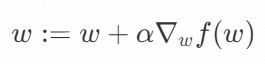
该公式将一直被迭代执行，直到达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
这里顺便提一嘴梯度下降算法，它与这里的梯度上升算法是一样的，只是公式中的加法需要变成减法。因此，对应的公式可以写成
，梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。
4. 代码实现
4.1 数据集可视化
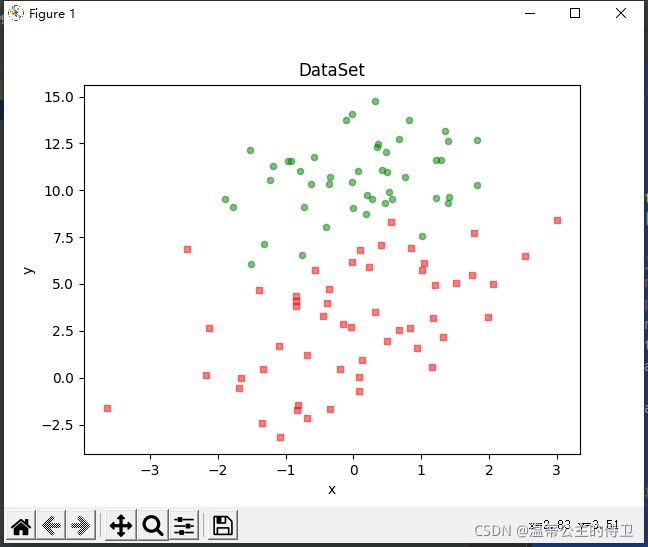
这里有一个数据集testSet.txt，样本总数为100个，每个点包含对应横纵坐标和类别标签，如图：
代码：
import numpy as np
import matplotlib.pyplot as plt
'''
函数说明：读取数据集
Returns:
dataMat：包含了数据特征值的矩阵
dataLabel：数据集的标签
'''
def loadDataSet():
dataMat = []
labelMat = []
fr = open('D:\迅雷下载\machinelearninginaction\Ch05\\testSet.txt')
for line in fr.readlines():
# strip()方法不传参时表示移除字符串首尾空格
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat, labelMat
"""
函数说明:绘制数据集
Parameters:
无
Returns:
无
"""
def plotDataSet():
dataMat, labelMat = loadDataSet()
# 转换成numpy的array数组
dataArr = np.array(dataMat)
n = np.shape(dataMat)[0]
# 正样本
xcord1 = [];
ycord1 = []
# 负样本
xcord2 = [];
ycord2 = []
# 根据数据集标签进行分类
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
plt.title('DataSet')
plt.xlabel('x');
plt.ylabel('y')
plt.show()
if __name__ == '__main__':
plotDataSet()
运行结果：
从上图可以看出我们采用的数据的分布情况。
4.2 使用梯度上升找到最佳参数
添加Sigmoid函数和Logistic回归梯度上升算法代码：
import numpy as np
import matplotlib.pyplot as plt
'''
函数说明：读取数据集
Returns:
dataMat：包含了数据特征值的矩阵
dataLabel：数据集的标签
'''
def loadDataSet():
dataMat = []
labelMat = []
fr = open('D:\迅雷下载\machinelearninginaction\Ch05\\testSet.txt')
for line in fr.readlines():
# strip()方法不传参时表示移除字符串首尾空格
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat, labelMat
"""
函数说明:绘制数据集
Parameters:
无
Returns:
无
"""
def plotDataSet():
dataMat, labelMat = loadDataSet()
# 转换成numpy的array数组
dataArr = np.array(dataMat)
n = np.shape(dataMat)[0]
# 正样本
xcord1 = [];
ycord1 = []
# 负样本
xcord2 = [];
ycord2 = []
# 根据数据集标签进行分类
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
plt.title('DataSet')
plt.xlabel('x');
plt.ylabel('y')
plt.show()
'''
函数说明：sigmoid函数
Parameters:
inx：经历一次前向传播还没有激活的值
Returns：
激活后的值
'''
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
"""
函数说明：梯度上升算法
Parameters:
dataMatIn：数据集
classLabels：数据标签
Returns:
weights：求得的权重数组(最优参数)
"""
def gradAscent(dataMatIn, classLabels):
# 将输入数据集转换为矩阵
dataMatrix = np.mat(dataMatIn)
LabelsMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
# 初始化系数矩阵，因为数据集为m行n列，所以权重矩阵为n行
weights = np.ones((n, 1))
# 迭代次数
maxIter = 500
# 步长(学习率)
alpha = 0.001
for k in range(maxIter):
h = sigmoid(dataMatrix * weights)
# 计算误差
error = LabelsMat - h
# 更新权重矩阵
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA()
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
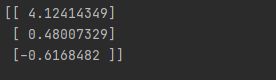
print(gradAscent(dataArr, labelMat))
if __name__ == '__main__':
plotDataSet()
运行结果：
该结果即为使用梯度上升算法找到的一组回归系数。
4.3 画出决策边界
已经解出了一组回归系数。现在开始绘制这个分隔线。
代码：
import numpy as np
import matplotlib.pyplot as plt
'''
函数说明：读取数据集
Returns:
dataMat：包含了数据特征值的矩阵
dataLabel：数据集的标签
'''
def loadDataSet():
dataMat = []
labelMat = []
fr = open('D:\迅雷下载\machinelearninginaction\Ch05\\testSet.txt')
for line in fr.readlines():
# strip()方法不传参时表示移除字符串首尾空格
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
fr.close()
return dataMat, labelMat
"""
函数说明:绘制数据集
Parameters:
无
Returns:
无
"""
def plotDataSet():
dataMat, labelMat = loadDataSet()
# 转换成numpy的array数组
dataArr = np.array(dataMat)
n = np.shape(dataMat)[0]
# 正样本
xcord1 = [];
ycord1 = []
# 负样本
xcord2 = [];
ycord2 = []
# 根据数据集标签进行分类
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
plt.title('DataSet')
plt.xlabel('x');
plt.ylabel('y')
plt.show()
'''
函数说明：sigmoid函数
Parameters:
inx：经历一次前向传播还没有激活的值
Returns：
激活后的值
'''
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
"""
函数说明：梯度上升算法
Parameters:
dataMatIn：数据集
classLabels：数据标签
Returns:
weights：求得的权重数组(最优参数)
"""
def gradAscent(dataMatIn, classLabels):
# 将输入数据集转换为矩阵
dataMatrix = np.mat(dataMatIn)
LabelsMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
# 初始化系数矩阵，因为数据集为m行n列，所以权重矩阵为n行
weights = np.ones((n, 1))
# 迭代次数
maxIter = 500
# 步长(学习率)
alpha = 0.001
for k in range(maxIter):
h = sigmoid(dataMatrix * weights)
# 计算误差
error = LabelsMat - h
# 更新权重矩阵
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA()
"""
函数说明：绘制数据集
Parameters:
weights：权重参数数组
Returns:
无
"""
def plotBestFit(wei):
dataMat, dataLabel = loadDataSet()
dataArray = np.array(dataMat)
xcord1 = [];
ycord1 = []
xcord2 = [];
ycord2 = []
n = np.shape(dataArray)[0]
for i in range(n):
if int(dataLabel[i]) == 0:
xcord1.append(dataArray[i, 1])
ycord1.append(dataArray[i, 2])
else:
xcord2.append(dataArray[i, 1])
ycord2.append(dataArray[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, color='red', marker='s', s=30)
ax.scatter(xcord2, ycord2, color='blue', s=30)
x = np.arange(-3.0, 3.0, 0.1)
y = (-wei[0, 0] - wei[1, 0] * x) / wei[2, 0]
ax.plot(x, y)
plt.xlabel('X1');
plt.ylabel('X2')
plt.show()
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
plotBestFit(weights)
运行结果：
可以看出只有两个蓝色样本被分错。
4.4 随机梯度上升算法
梯度上升算法在每次更新回归系数时都需要遍历整个数据集，该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。
一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为 随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应，一次处理所有数据被称作是“批处理”。
改进算法还增加了一个迭代次数作为第3个参数。如果该参数没有给定的话，算法将默认迭代150次。如果给定，那么算法将按照新的参数值进行迭代。代码如下：
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random
'''
Parameters:
无
Returns:
dataMat - 数据列表
labelMat - 标签列表
'''
# 函数说明:加载数据
def loadDataSet():
dataMat = [] # 创建数据列表
labelMat = [] # 创建标签列表
fr = open('D:\迅雷下载\machinelearninginaction\Ch05\\testSet.txt') # 打开文件
for line in fr.readlines(): # 逐行读取
lineArr = line.strip().split() # 去回车，放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 添加数据
labelMat.append(int(lineArr[2])) # 添加标签
fr.close() # 关闭文件
return dataMat, labelMat # 返回
'''
Parameters:
inX - 数据
Returns:
sigmoid函数
'''
# 函数说明:sigmoid函数
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
'''
Parameters:
weights - 权重参数数组
Returns:
无
'''
# 函数说明:绘制数据集
def plotBestFit(weights):
dataMat, labelMat = loadDataSet() # 加载数据集
dataArr = np.array(dataMat) # 转换成numpy的array数组
n = np.shape(dataMat)[0] # 数据个数
xcord1 = [];
ycord1 = [] # 正样本
xcord2 = [];
ycord2 = [] # 负样本
for i in range(n): # 根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2]) # 1为正样本
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2]) # 0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) # 添加subplot
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5) # 绘制正样本
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5) # 绘制负样本
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') # 绘制title
plt.xlabel('X1');
plt.ylabel('X2') # 绘制label
plt.show()
'''
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
'''
# 函数说明:改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = np.shape(dataMatrix) # 返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) # 参数初始化
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.01 # 降低alpha的大小，每次减小1/(j+i)。
randIndex = int(random.uniform(0, len(dataIndex))) # 随机选取样本
h = sigmoid(sum(dataMatrix[randIndex] * weights)) # 选择随机选取的一个样本，计算h
error = classLabels[randIndex] - h # 计算误差
weights = weights + alpha * error * dataMatrix[randIndex] # 更新回归系数
del (dataIndex[randIndex]) # 删除已经使用的样本
return weights # 返回
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights = stocGradAscent1(np.array(dataMat), labelMat)
plotBestFit(weights)
运行结果：
4.5 回归系数与迭代次数的关系
可以看到分类效果也是不错的。不过，从这个分类结果中，不好看出迭代次数和回归系数的关系，也就不能直观的看到每个回归方法的收敛情况。因此，编写程序，绘制出回归系数和迭代次数的关系曲线：
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random
'''
Parameters:
无
Returns:
dataMat - 数据列表
labelMat - 标签列表
'''
# 函数说明:加载数据
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车，放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
'''
Parameters:
inX - 数据
Returns:
sigmoid函数
'''
# 函数说明:sigmoid函数
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
'''
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
'''
# 函数说明:梯度上升算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组，返回权重数组
'''
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
'''
# 函数说明:改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) #参数初始化
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小，每次减小1/(j+i)。
randIndex = int(random.uniform(0,len(dataIndex))) #随机选取样本
h = sigmoid(sum(dataMatrix[randIndex]*weights)) #选择随机选取的一个样本，计算h
error = classLabels[randIndex] - h #计算误差
weights = weights + alpha * error * dataMatrix[randIndex]#更新回归系数
del(dataIndex[randIndex]) #删除已经使用的样本
return weights #返回
'''
Parameters:
weights_array1 - 回归系数数组1
weights_array2 - 回归系数数组2
Returns:
无
'''
# 函数说明:绘制回归系数与迭代次数的关系
def plotWeights(weights_array1,weights_array2):
#设置汉字格式
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
#将fig画布分隔成1行1列,不共享x轴和y轴,fig画布的大小为(13,8)
#当nrow=3,nclos=2时,代表fig画布被分为六个区域,axs[0][0]表示第一行第一列
fig, axs = plt.subplots(nrows=3, ncols=2,sharex=False, sharey=False, figsize=(20,10))
x1 = np.arange(0, len(weights_array1), 1)
#绘制w0与迭代次数的关系
axs[0][0].plot(x1,weights_array1[:,0])
axs0_title_text = axs[0][0].set_title(u'梯度上升算法：回归系数与迭代次数关系',FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
#绘制w1与迭代次数的关系
axs[1][0].plot(x1,weights_array1[:,1])
axs1_ylabel_text = axs[1][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
#绘制w2与迭代次数的关系
axs[2][0].plot(x1,weights_array1[:,2])
axs2_xlabel_text = axs[2][0].set_xlabel(u'迭代次数',FontProperties=font)
axs2_ylabel_text = axs[2][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
x2 = np.arange(0, len(weights_array2), 1)
#绘制w0与迭代次数的关系
axs[0][1].plot(x2,weights_array2[:,0])
axs0_title_text = axs[0][1].set_title(u'改进的随机梯度上升算法：回归系数与迭代次数关系',FontProperties=font)
axs0_ylabel_text = axs[0][1].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
#绘制w1与迭代次数的关系
axs[1][1].plot(x2,weights_array2[:,1])
axs1_ylabel_text = axs[1][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
#绘制w2与迭代次数的关系
axs[2][1].plot(x2,weights_array2[:,2])
axs2_xlabel_text = axs[2][1].set_xlabel(u'迭代次数',FontProperties=font)
axs2_ylabel_text = axs[2][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights1,weights_array1 = stocGradAscent1(np.array(dataMat), labelMat)
weights2,weights_array2 = gradAscent(dataMat, labelMat)
plotWeights(weights_array1, weights_array2)
运行结果：
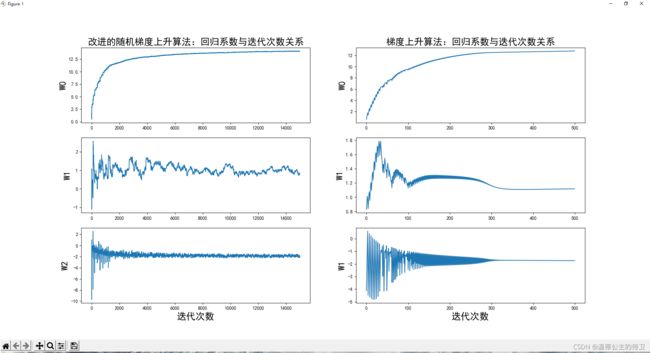
改进的随机梯度上升算法，在遍历数据集的第20次开始收敛。而梯度上升算法，在遍历数据集的第300次才开始收敛。对比之下，明显改进的随机梯度算法会更加优化一点。
5. 从疝气病症预测病马死亡率
5.1 准备数据
此部分使用的数据集共366个样本和28个特征，其中299个样本作为训练集，67个样本作为测试集（注：这里使用的数据集均已经过预处理，例如：数据中的缺失值用一个实数值来代替、丢弃类别标签已经缺失的样本），原始的数据集经过预处理后保存成两个文件：horseColicTraining.txt和horseColicTest.txt
预处理数据做两件事：
- 如果测试集中一条数据的特征值已经确实，那么我们选择实数0来替换所有缺失值，因为本文使用Logistic回归。因此这样做不会影响回归系数的值。sigmoid(0)=0.5，即它对结果的预测不具有任何倾向性。
- 如果测试集中一条数据的类别标签已经缺失，那么我们将该类别数据丢弃，因为类别标签与特征不同，很难确定采用某个合适的值来替换。
5.2 测试算法：用Logistic 回归进行分类
使用逻辑回归方法进行分类时需把测试集上每个特征向量乘以最优化方法得到回归系数，再将该乘积结果求和，最后输入到Sigmoid函数中即可。如果对应的Sigmoid值大于0.5就预测类别标签为1，否则为0。
代码：
from math import exp
import numpy as np
import random
'''
Parameters:
inX - 数据
Returns:
sigmoid函数
'''
# 函数说明:sigmoid函数
def sigmoid(inX):
if inX >= 0: # 对sigmoid函数的优化，避免了出现极大的数据溢出
return 1.0 / (1 + exp(-inX))
else:
return exp(inX) / (1 + exp(inX))
'''
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
'''
# 函数说明:改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = np.shape(dataMatrix) # 返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) # 参数初始化
# 存储每次更新的回归系数
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.01 # 降低alpha的大小，每次减小1/(j+i)。
randIndex = int(random.uniform(0, len(dataIndex))) # 随机选取样本
h = sigmoid(sum(dataMatrix[randIndex] * weights)) # 选择随机选取的一个样本，计算h
error = classLabels[randIndex] - h # 计算误差
weights = weights + alpha * error * dataMatrix[randIndex] # 更新回归系数
del (dataIndex[randIndex]) # 删除已经使用的样本
return weights # 返回
# 函数说明:使用Python写的Logistic分类器做预测
def colicTest():
frTrain = open('D:\迅雷下载\machinelearninginaction\Ch05\\horseColicTraining.txt') # 打开训练集
frTest = open('D:\迅雷下载\machinelearninginaction\Ch05\\horseColicTest.txt') # 打开测试集
trainingSet = [];
trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500) # 使用改进的随即上升梯度训练
errorCount = 0;
numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine) - 1):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[-1]):
errorCount += 1
errorRate = (float(errorCount) / numTestVec) * 100 # 错误率计算
print("测试集错误率为: %.2f%%" % errorRate)
'''
Parameters:
inX - 特征向量
weights - 回归系数
Returns:
分类结果
'''
# 函数说明:分类函数
def classifyVector(inX, weights):
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
if __name__ == '__main__':
colicTest()
运行结果：
可以看得出来，错误率还是相对来说比较高的，为什么会出现这种情况呢？有部分原因是因为数据集本身有部分数据缺失，这是无法避免的，另一个原因是，我们使用的是改进后的随机梯度上升算法，这个算法对于数据集比较小的样本是不太合适的。
6. 实验小结
Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。
随机梯度上升算法与梯度上升算法的效果相当，但占用更少的计算资源。此外，随机梯度上升是一个在线算法，它可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批处理运算。
机器学习的一个重要问题就是如何处理缺失数据。这个问题没有标准答案，取决于实际应用中的需求。现有一些解决方案，每种方案都各有优缺点。