PyTorch量化实践(1)
翻译来源https://pytorch.org/blog/quantization-in-practice/
量化是一种廉价而简单的方法,可以使深度神经网络模型运行得更快,并具有更低的内存需求。PyTorch提供了几种量化模型的不同方法。在这篇博客文章中,我们将(快速)为深度学习中的量化奠定基础,然后看看每种技术在实践中是怎样的。最后,我们将以文献中关于在工作流程中使用量化的建议作为结束。
量化原理
如果有人问你几点了,你不会回答“10:14:34:430705”,而会说“10点过一刻”。
量化本质是信息压缩,在深度网络中,它指的是降低其权重和/或激活的数值精度。
过度参数化的深度神经网络(DNN)有更多的自由度,这使它们成为信息压缩的好候选者[1]。当你量化一个模型时,通常会发生两件事——模型变得更小,运行效率更高。硬件供应商明确地允许更快地处理8位数据(相比32位数据),从而获得更高的吞吐量。更小的模型具有更低的内存占用和功耗[2],这对于在边缘部署至关重要。
函数映射
映射函数是一个将值从浮点空间映射到整数空间的函数。常用的映射函数是由给出的线性变换 Q ( r ) = round ( r / S + Z ) Q(r)=\operatorname{round}(r / S+Z) Q(r)=round(r/S+Z),其中 r r r是输入, S S S和 Z Z Z是量化参数。
为了重新转换为浮点空间,相对应的逆函数则是 r ~ = ( Q ( r ) − Z ) ⋅ S , r ~ ≠ r \tilde{r}=(Q(r)-Z) \cdot S,\tilde{r}≠r r~=(Q(r)−Z)⋅S,r~=r,它们之间的差构成了量化误差。
量化参数
映射函数由比例因子 S S S和零点参数(zero-point) Z Z Z构成,其中, S S S就是输入和输出范围的比值,有 S = β − α β q − α q S=\frac{\beta-\alpha}{\beta_{q}-\alpha_{q}} S=βq−αqβ−α,其中, [ α , β ] [\alpha,\beta] [α,β]是输入的裁剪范围,即允许输入的边界。而 [ α q , β q ] [\alpha_q,\beta_q] [αq,βq]则是映射的量化输出空间的范围,例如8bit的量化,输出的范围 β q − α q < = ( 2 8 − 1 ) \beta_{q}-\alpha_{q}<=(2^8-1) βq−αq<=(28−1)
Z Z Z作为偏差,以确保输入空间中的0完美地映射到量化空间中的0,有 Z = − ( α S − α q ) Z=-\left(\frac{\alpha}{S}-\alpha_{q}\right) Z=−(Sα−αq)
校准
选择输入剪切范围的过程称为校准。最简单的技术(也是PyTorch的默认方法)是记录运行的最小值和最大值,并将它们赋给 α \alpha α和 β \beta β。TensorRT也使用熵最小化(KL散度),均方误差最小化,或输入范围的百分比。
在PyTorch中,Observer模块(docs, code)收集输入值的统计信息并计算量化参数 S S S和 Z Z Z。不同的校准方案会产生不同的量化输出,最好通过经验验证哪种方案最适合应用程序和架构(稍后会详细介绍)。
from torch.quantization.observer import MinMaxObserver, MovingAverageMinMaxObserver, HistogramObserver
C, L = 3, 4
normal = torch.distributions.normal.Normal(0,1)
inputs = [normal.sample((C, L)), normal.sample((C, L))]
print(inputs)
# >>>>>
# [tensor([[-0.0590, 1.1674, 0.7119, -1.1270],
# [-1.3974, 0.5077, -0.5601, 0.0683],
# [-0.0929, 0.9473, 0.7159, -0.4574]]]),
# tensor([[-0.0236, -0.7599, 1.0290, 0.8914],
# [-1.1727, -1.2556, -0.2271, 0.9568],
# [-0.2500, 1.4579, 1.4707, 0.4043]])]
observers = [MinMaxObserver(), MovingAverageMinMaxObserver(), HistogramObserver()]
for obs in observers:
for x in inputs: obs(x)
print(obs.__class__.__name__, obs.calculate_qparams())
# >>>>>
# MinMaxObserver (tensor([0.0112]), tensor([124], dtype=torch.int32))
# MovingAverageMinMaxObserver (tensor([0.0101]), tensor([139], dtype=torch.int32))
# HistogramObserver (tensor([0.0100]), tensor([106], dtype=torch.int32))
仿射和对称量子化方案
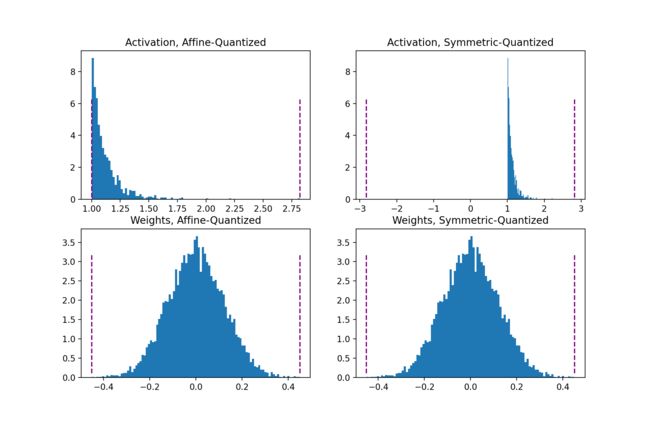
仿射或非对称量化方案将输入范围分配给最小和最大观测值。仿射方案通常使用更紧密的范围,对于量化非负激活非常有用(如果输入张量从不为负,则不需要输入范围包含负值)。范围有 α = m i n ( r ) , β = m a x ( r ) \alpha=min(r),\beta=max(r) α=min(r),β=max(r)。当用于权重张量[3]时,仿射量化导致了更大的计算推断花销。
对称量化方案将输入范围集中在0附近,消除了计算零点偏移的需要。范围计算为 − α = β = m a x ( ∣ m i n ( r ) ∣ , ∣ m a x ( r ) ∣ ) -\alpha=\beta=max(|min(r)|,|max(r)|) −α=β=max(∣min(r)∣,∣max(r)∣)。对于倾斜信号(如非负激活),这可能导致糟糕的量化分辨率,因为范围可能包括从未在输入中显示的值。
总结来说,非对称量化对非负激活有用,对权重张量量化则计算开销较大;而对称量化方案对非负激活可能会很糟糕。
act = torch.distributions.pareto.Pareto(1, 10).sample((1,1024))
weights = torch.distributions.normal.Normal(0, 0.12).sample((3, 64, 7, 7)).flatten()
def get_symmetric_range(x):
beta = torch.max(x.max(), x.min().abs())
return -beta.item(), beta.item()
def get_affine_range(x):
return x.min().item(), x.max().item()
def plot(plt, data, scheme):
boundaries = get_affine_range(data) if scheme == 'affine' else get_symmetric_range(data)
a, _, _ = plt.hist(data, density=True, bins=100)
ymin, ymax = np.quantile(a[a>0], [0.25, 0.95])
plt.vlines(x=boundaries, ls='--', colors='purple', ymin=ymin, ymax=ymax)
fig, axs = plt.subplots(2,2)
plot(axs[0, 0], act, 'affine')
axs[0, 0].set_title("Activation, Affine-Quantized")
plot(axs[0, 1], act, 'symmetric')
axs[0, 1].set_title("Activation, Symmetric-Quantized")
plot(axs[1, 0], weights, 'affine')
axs[1, 0].set_title("Weights, Affine-Quantized")
plot(axs[1, 1], weights, 'symmetric')
axs[1, 1].set_title("Weights, Symmetric-Quantized")
plt.show()
在PyTorch中,你可以在初始化Observer时指定仿射或对称方案。注意,并不是所有的obeserver都支持这两种模式。
for qscheme in [torch.per_tensor_affine, torch.per_tensor_symmetric]:
obs = MovingAverageMinMaxObserver(qscheme=qscheme)
for x in inputs: obs(x)
print(f"Qscheme: {qscheme} | {obs.calculate_qparams()}")
# >>>>>
# Qscheme: torch.per_tensor_affine | (tensor([0.0101]), tensor([139], dtype=torch.int32))
# Qscheme: torch.per_tensor_symmetric | (tensor([0.0109]), tensor([128]))
逐张量和逐信道量化方案
量化参数可以作为一个整体计算层的整个权张量,也可以单独计算每个通道的权张量。在逐张量中,相同的剪切范围应用于一层中的所有通道
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m6yuuvXT-1653633614929)(https://pytorch.org/assets/images/quantization-practice/per-channel-tensor.svg)]
图3所示。每通道为每个通道使用一组量化参数。每个张量对整个张量使用相同的量化参数。对于权重量化,对称每通道量化提供了更好的准确性;每张量量化表现不佳,可能是由于batchnorm折叠[3]跨通道的卷积权值的高方差。
from torch.quantization.observer import MovingAveragePerChannelMinMaxObserver
obs = MovingAveragePerChannelMinMaxObserver(ch_axis=0) # calculate qparams for all `C` channels separately
for x in inputs: obs(x)
print(obs.calculate_qparams())
# >>>>>
# (tensor([0.0090, 0.0075, 0.0055]), tensor([125, 187, 82], dtype=torch.int32))
后端引擎
目前,量化操作符通过FBGEMM后端运行在x86机器上,或者在ARM机器上使用QNNPACK原语。对服务器gpu的后端支持(通过TensorRT和cuDNN)即将到来。了解有关将量化扩展到自定义后端的更多信息:RFC-0019。
backend = 'fbgemm' if x86 else 'qnnpack'
qconfig = torch.quantization.get_default_qconfig(backend)
torch.backends.quantized.engine = backend
QConfig
QConfig存储Observer和用于量化激活和权重的量化方案。
确保传递的是Observer类(而不是实例),或者可以返回Observer实例的可调用对象。使用with_args()覆盖默认参数。
my_qconfig = torch.quantization.QConfig(
activation=MovingAverageMinMaxObserver.with_args(qscheme=torch.per_tensor_affine),
weight=MovingAveragePerChannelMinMaxObserver.with_args(qscheme=torch.qint8)
)
# >>>>>
# QConfig(activation=functools.partial(, qscheme=torch.per_tensor_affine){}, weight=functools.partial(, qscheme=torch.qint8){})