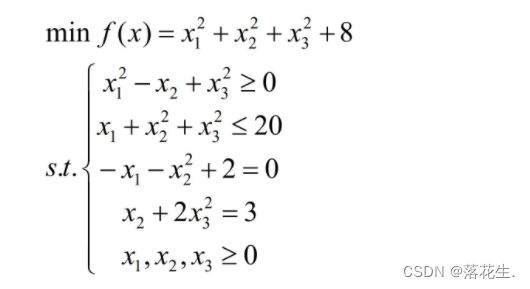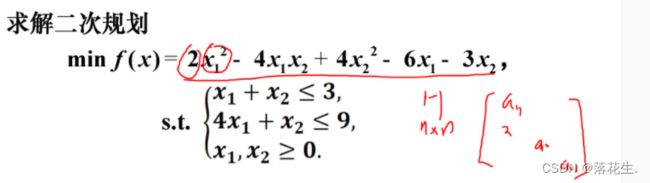学习非线性规划和二次规划
非线性规划
非线性规划模型(NP)
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不像线性规划有单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。



非线性规划的数学模型
列
%将以下代码分别复制到MATLAB® 路径上名为fun1.m和fun3.m 的文件中。
% fun1.m内容
% function f=fun1(x)
% f=sum(x.^2)+8;
% fun3.m内容
% function [g,h]=fun3(x)
% g=[-x(1)^2+x(2)-x(3)^2
% x(1)+x(2)^2+x(3)^3-20];
% h=[-x(1)-x(2)^2+2
% x(2)+2*x(3)^2-3];
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun3')%主代码仅仅只有这一行
运行结果

这段老师给的代码一开始并没有成功运行,因为将所有的函数都放在同一个脚本里了,导致函数定义和引用失败
笔者自己在不能运行上述代码的情况下自己编辑了一段代码
fun=@(x)x(1)^2+x(2)^2+x(3)^2+8;
A=[];
b=[];
Aeq=[];
beq=[];
x0=rand(3,1);
nonlcon=@fun2; %调用了路径为fun.2的函数
%函数fun.2内容
% function [c,ceq]=fun2(x)
% c=[-x(1)^2+x(2)-x(3)^2
% x(1)+x(2)^2+x(3)^3-20];
% ceq=[-x(1)-x(2)^2+2
% x(2)+2*x(3)^2-3];
x=fmincon(fun,x0,A,b,Aeq,beq,zeros(3,1),[],nonlcon)
运行结果

笔者自己编写的代码虽然也能解出x的最优解,但并没有直接求出y的解。但在笔者编写此代码时,成功的创建和引用了函数fun2,这一点启发笔者想到第一段代码为何运行失败,后经过改正第一段代码得以成功运行。
二次规划

Matlab
中求解二次规划的命令是
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
返回值x是决策向量x的值,返回值fval是目标函数在x处的值(具体细节可以参看在Matlab命令窗口中运行help quadprog后的帮助)
例子
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))
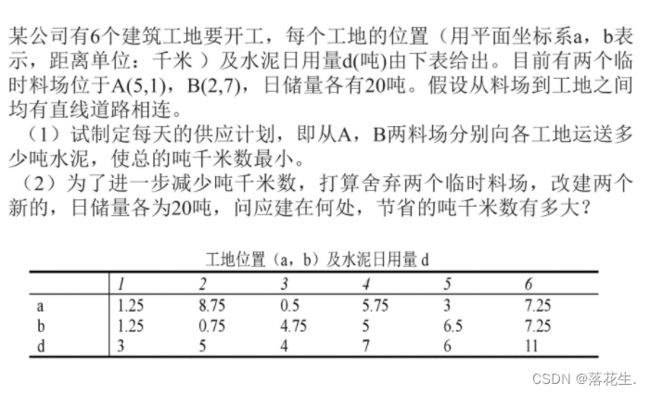
应用实例:供应与选址
建立模型
使用临时料场的情形
第一问的解决
代码
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
d=[3 5 4 7 6 11];
x=[5 2];
y=[1 7];
e=[20 20];
for i=1:6
for j=1:2
aa(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2);
end
end %计算每个料场到每个工地的距离
CC=[aa(:,1);aa(:,2)]';%将两个料场到每个工地的距离以12维列向量的形式存放
A=[1 1 1 1 1 1 0 0 0 0 0 0;0 0 0 0 0 0 1 1 1 1 1 1];
B=[20;20];%每个料场提供的水泥小于20吨
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0;
0 1 0 0 0 0 0 1 0 0 0 0;
0 0 1 0 0 0 0 0 1 0 0 0;
0 0 0 1 0 0 0 0 0 1 0 0;
0 0 0 0 1 0 0 0 0 0 1 0;
0 0 0 0 0 1 0 0 0 0 0 1];
beq=[d(1);d(2);d(3);d(4);d(5);d(6)];%两个料场向同一工厂提供的水泥等于该工厂日用量
VLB=[0 0 0 0 0 0 0 0 0 0 0 0];%下限
VUB=[];%上限
x0=[1 2 3 0 1 0 0 1 0 1 0 1];%初始值
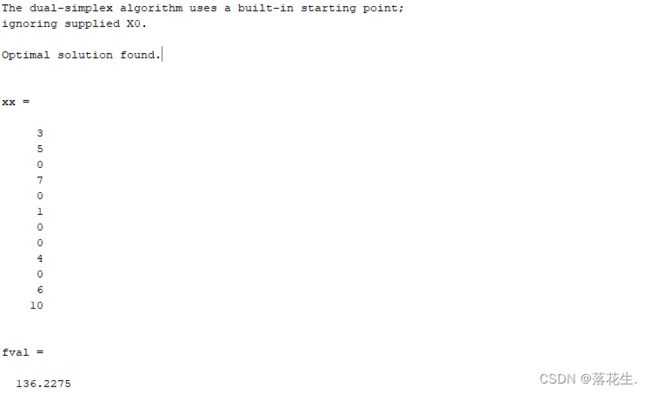
[xx,fval]=linprog(CC,A,B,Aeq,beq,VLB,VUB,x0)%返回目标函数在解 xx处的值:fval = f'*x
改建两个新料场的情形

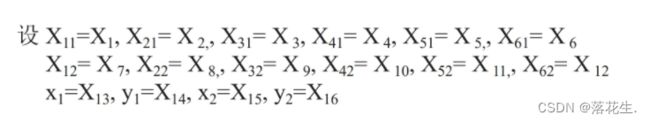
这里依旧需要两步
先创建m文件liaochang.m去定义目标函数
取初值x0并编辑主程序
初值选择的不同,会导致最后收敛的结果不同。一般会随机生成出初值,然后运行产生结果,将结果作为初值重新编译运行代码。如果取得的结果更优,则重复上述步骤。如果没有取得更优结果,则默认结果为最优结果
代码
%将以下代码分别复制到MATLAB® 路径上名为liaochang.m 的文件中
% function f=liaochang(x)
% a=[1.25 8.75 0.5 5.75 3 7.25];
% b=[1.25 0.75 4.75 5 6.5 7.75];
% d=[3 5 4 7 6 11];
% e=[20 20];
% f1=0;
% for i=1:6
% s(i)=sqrt((x(13)-a(i))^2+(x(14)-b(i))^2);
% f1=s(i)*x(i)+f1;
% end
% f2=0;
% for i=7:12
% s(i)=sqrt((x(15)-a(i-6))^2+(x(16)-b(i-6))^2);
% f2=s(i)*x(i)+f2;
% end
% f=f1+f2;
%主代码
x0=[3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7]';
A=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B=[20;20];
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0];
beq=[3;5;4;7;6;11];
vlb=[zeros(12,1);-inf;-inf;-inf;-inf];
vub=[];
[x,fval,exitflag]=fmincon('liaochang',x0,A,B,Aeq,beq,vlb,vub)
解决非线性问题依旧需要创建和引用目标函数
运行结果
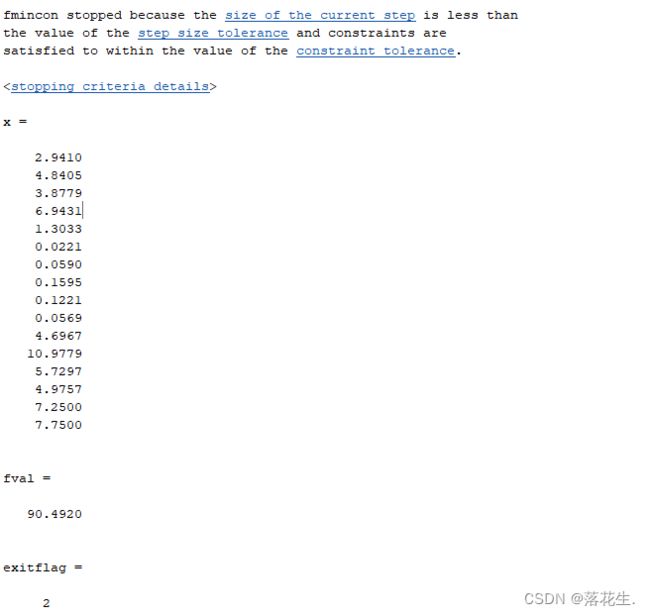
[x,fval,exitflag,output] = fmincon(___) 还返回描述 fmincon 的退出条件的值 exitflag,以及提供优化过程信息的结构体 output。
使用额外输出检查,要轻松检查解的质量,可请求 exitflag 和 output 输出。
exitflag 值 1 表示该解是局部最小值。
output 结构体报告有关求解过程的几个统计量。具体来说,它在 output.iterations 中给出迭代次数,在 output.funcCount 中给出函数计算次数,以及在 output.constrviolation 中给出可行性。