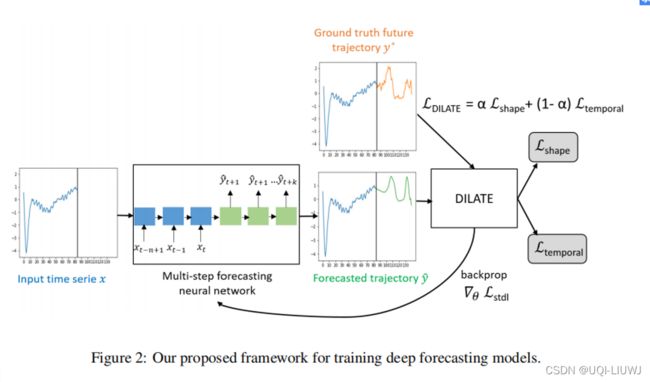
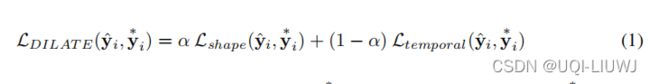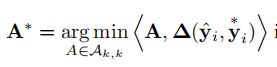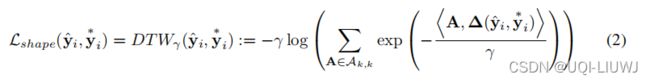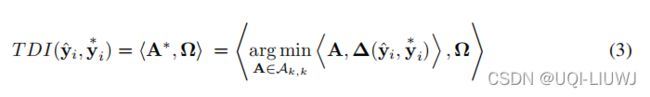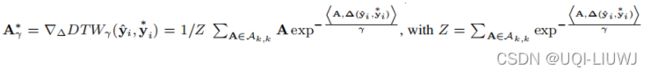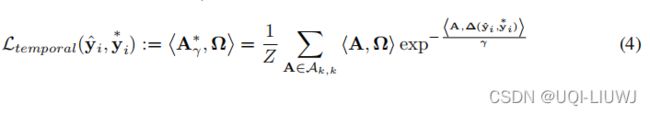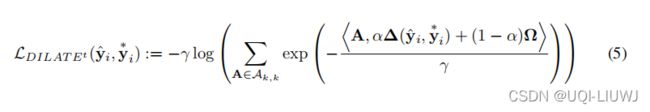论文笔记 Shape and Time Distortion Loss for Training DeepTime Series Forecasting Models

该论文的poster

DILATE/poster_DILATE.pdf at master · vincent-leguen/DILATE (github.com)

0 摘要

        本文解决了非平稳信号的时间序列预测和多个未来步骤预测的问题。为了处理这个具有挑战性的任务，我们引入了 DILATE（包括形状和时间的失真损失，DIstortion Loss including shApe and TimE），这是一种用于训练深度神经网络的新目标函数。

         DILATE 旨在准确预测突然变化，并明确结合了支持精确形状和时间变化检测的两个术语。

        我们引入了一种适用于训练深度神经网络的可微损失函数，并提供了一个自定义的反向支持实现来加速优化。

        我们还介绍了 DILATE 的变体，它提供了DTW)的平滑泛化。

        DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现）_UQI-LIUWJ的博客-CSDN博客

        在各种非平稳数据集上进行的实验表明，与使用标准均方误差 (MSE) 损失函数以及 DTW 和DTW衍生的损失函数  的模型相比，DILATE 的行为非常好。

         DILATE 也与模型的选择无关，我们强调了它对训练完全连接的网络以及专门的循环架构的好处，表明它有能力改进最先进的轨迹预测方法。

1 introduction

        这项工作的重点是非平稳信号的多步预测问题，即当未来数据不能仅从过去的周期性中推断出来，以及何时可能发生突然变化是未知的。

        这在很多重要和多样化的应用领域都适用，例如 调节电力消耗 [63, 36]，预测可再生能源生产 [23] 或交通流量 [35, 34] 的急剧中断，心电图 (ECG) 分析 [9]，股票市场预测 [14] 等。

        由于深度神经网络能够对复杂的非线性时间依赖性进行建模，因此深度学习是解决这种多步骤和非平稳预测问题的一种有吸引力的解决方案。

         最近提出了许多方法，主要依赖于在直接多步模型 [3]（如Seq2Seq [ 34, 60, 57, 61] 或用于概率预测的状态空间模型 [44, 40]  ）

         关于训练，绝大多数方法使用均方误差（MSE）或其变体（MAE等）作为损失函数。 然而，在我们的上下文中，依赖 MSE 可能是不够的，如图 1 所示。

     

        这里，目标曲线（ground truth）是一个阶跃函数（蓝色），我们提出了三种预测曲线，如图 1(a),(b) 和 (c)所示，与目标相比具有相似的 MSE 损失，但预测效果却大不相同。

• 预测 (a) 不足以用于监管目的，因为它没有捕捉到即将到来的急剧下跌。
• 预测（b）和（c）更好地状态了的变化，因为确实可以预料到急剧下降，尽管有轻微的延迟（b）或幅度略有不准确（c）。

        本文介绍了 DILATE（包括 shaApe 和 TimE 的失真损失），这是一种用于在多步和非平稳时间序列预测的背景下训练深度神经网络的新目标函数。

        DILATE 明确地将与形状相关的惩罚，和变化检测的时间定位误差分成两个术语（第 3 节）。

        DILATE 的效果也图 1 中展示了：形状和时间损失的值在图 1(a) 中很大，而形状项在图 1(b) 中很小，时间项在图 1 (c)中很小。

         DILATE 结合了形状和时间项，因此能够为预测 (b) 和 (c) 输出比 (a) 小得多的损失，正如预期的那样。

         为了用 DILATE 训练深度神经网络，我们为形状和时间项设计了一个可微的损失函数（第 3.1 节），以及一个用于加速优化的有效和自定义的反向支持实现（第 3.2 节）。

        我们还介绍了 DILATE 的一种变体，它提供了DTW指标的平滑泛化 [43, 28]。

        在几个合成和真实非平稳数据集上进行的实验表明，使用 DILATE 训练的模型在使用形状和时间失真指标评估时明显优于使用 MSE 损失函数训练的模型，而使用 MSE 评估时使用 DILATE 训练的模型也保持非常好的性能。

        最后，我们展示了 DILATE 可以与各种网络架构一起使用，并且可以在形状和时间指标上优于专为多步和非平稳预测设计的最新模型。

 2 相关工作

2.1 时间序列预测

        时间序列预测的传统方法包括线性自回归模型，例如 ARIMA 模型 [6] 和指数平滑 [27]，它们都属于线性状态空间模型 (SSM) [17] 的广义类别。这些方法处理线性动态和平稳时间序列（或因差分而变得平稳）。然而，对于许多可能呈现分布突然变化的现实世界时间序列，平稳性假设并不满足。

        此后，循环神经网络 (RNN) 和长短期记忆网络 (LSTM) [25] 等变体因其自动特征提取能力、复杂模式和长期依赖建模而变得流行。

        在深度学习时代，最近通过利用注意力机制 [30, 39, 50, 12] 或张量分解 [60, 58, 46] 致力于解决具有大量输入序列 [31] 的多元时间序列预测， 用于捕获系列之间的共享信息。

        当前的另一个趋势是结合深度学习和状态空间模型来建模不确定性 [45、44、40、56]。

        在本文中，我们专注于确定性多步预测。最常见的方法是递归地应用一步训练好的模型。

        尽管单步学习模型可以针对多步设置进行调整和改进 [55]，但对不同多步策略 [48] 的彻底比较后，直接多步预测策略更好。

        在这一类别中特别突出的是序列到序列 (Seq2Seq) RNN 模型 1[44, 31, 60, 57, 19]，它在机器翻译方面取得了巨大成功。

        Seq2Seq 预测的理论泛化界限是用一个额外的差异项来量化时间序列的非平稳性 [29]。

        随着 WaveNet 在音频生成方面的成功 [53]，具有扩张的卷积神经网络已成为时间序列预测的流行替代方案 [5]。

        自注意力 Transformer 架构 [54] 最近也被研究用于访问远程上下文，而不管距离如何 [32]。

        我们强调，我们提出的损失函数可用于训练任何直接的多步深度架构。  

2.2 评估和训练指标

        训练和评估深度模型的主要损失函数是 MAE、MSE 及其变体（SMAPE 等）。

        反映形状和时间定位的指标有：

• 形状：Dynamic Time Warping [43]；
• 时序错误可以通过在通过变化点检测 [8, 33] 分割序列后，计算精度和召回分数，
• 时序也通过计算两组变化点 [22, 51] 之间的 Hausdorff 距离来转换为检测问题。

然而，这些评估指标是不可微分的，这使得它们无法用作训练深度神经网络的损失函数。

3 使用DILATE 训练DNN

我们考虑一个有N个输入的时间序列A， （可以看成N个变量）

其中每一个输入长度为n，（可以看成时间序列长度为n，每个时刻有p维属性）

 一个预测模型预测未来k步的时间序列

假设未来k步的ground truth  为

那么DiLATE的目标函数为：

 3.0 符号和定义

        和 都是基于对齐的预测值 

和实际值 

        与此同时，我们定义一个矩阵，其中如果和是有关联的，那么，否则为0【联想：DTW中的最佳路径是否经过(h,j)这个点】

        相应地，我们记为逐对开销矩阵，其中δ表示和之间的相异程度（比如欧几里得矩阵）

 3.1 形状和时域项目

我们的形状损失函数基于DTW[43]，对应于以下优化问题

DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现）_UQI-LIUWJ的博客-CSDN博客

       

是 和 之间的最佳连接路径

        通过在时间维度上上对齐预测的和 ground truth的 时间序列，DTW 损失主要关注信号之间的结构形状差异。

        然而，已知 DTW 是不可微分的（因为min函数不具有微分结果）。 因而我们使用min 的平滑算子来定义我们的可微形状项

 

（也即soft-DTW）

机器学习笔记 soft-DTW（论文笔记 A differentiable loss function for time-series）_UQI-LIUWJ的博客-CSDN博客

 3.2 时间项

 我们的第二项旨在惩罚和 之间的时间失真

 我们的分析基于 和 之间的最优DTW路径A*

我们的损失函数的灵感来自于计算时间失真指数 (TDI) 以进行时间错位估计 [20, 52]，它基本上包括计算最佳 DTW 路径 A* 与第一条对角线之间的偏差。

 我们首先用我们的符号重写了一个广义的 TDI 损失函数

 （也就是得到的这个DTW的path和对角线之间的差距）【得到的DTW这个path上的之和】

Ω是一个k×k的方阵，它用来惩罚h≠j的和

在我们的实验中，我们令

当然，先验知识也可以包含在 Ω 矩阵结构中，比如在j前面的Ω更大，在j后面的Ω更小等

        但是 公式（3）中的TDI loss也是不可微的，这里我们不能用和3.1一样的平滑方式， 因为最小化涉及两个不同的量 Ω 和 Δ

        我们使用来定义argmin算子的平滑近似

        把A*算出来，有：

 

 基于这个平滑的A*，我们有平滑的空间loss：

 

 3.3 DILATE有效的前向传播和反向传播

        由于的基数随 k 呈指数增长，直接计算等式 (2) 和等式 (4) 中的形状和时间损失是难以处理的。

        我们提供了前向和后向传递的高效实现，以提高学习效率。

3.3.1 shape loss

        论文采用了和soft-dtw一致的思路（前向传播和反向传播）

机器学习笔记 soft-DTW（论文笔记 A differentiable loss function for time-series）_UQI-LIUWJ的博客-CSDN博客

3.3.2 temporal loss

        对于，等式 (4) 中前向传播的瓶颈是计算，我们按照 Lshape 反向传播的思路来实现它。（也即soft-dtw中的E矩阵）

        而对于反向传播，由于会遇到Hessian矩阵的计算，这个论文中只是提了一嘴：一样可以使用动态规划实现，我这里就展开说一下。

        对于复合函数的二阶导，一样有链式法则

        数学知识复习：二阶导复合函数的链式法则_UQI-LIUWJ的博客-CSDN博客

所以我们这里

•  和 就是两个已知矩阵和x之间的雅可比矩阵/何塞矩阵
• 在soft-dtw里面已经求得了
•  ，也就是和之间的雅可比矩阵

 3.4 dilate 变体

我们之前的DILATE是

我们结合形状和时间惩罚的方法的一种变体是将时间项合并到方程（2）中的平滑 Lshape 函数中

        等式 (5) 中的能够结合形状和时间标准训练具有平滑损失的深度神经网络。 然而，对解开形状和时间误差的能力有限，因为最佳路径是根据形状和时间项计算的。

         相比之下，我们在等式 (1) 中的损失将损失分为形状和时间两个错位分量，时间惩罚应用于最佳无约束 DTW 路径。 我们通过实验验证我们的优于其“纠结”版本

4 实验部分

4.1 实验配置

4.1.1 数据集

        为了说明 DILATE 的相关性，我们对来自不同领域的 3 个非平稳时间序列数据集进行了实验

• 合成（k = 20）数据集：包括基于由两个峰值组成的输入信号预测突然变化（阶跃函数）。

        这种受控设置旨在精确测量预测的形状和时间误差。

        我们生成 500 个时间序列用于训练，500 个用于验证，500 个用于测试。

        数据一共有 40 个时间步长：前 20 个是输入，后 20 个是要预测的目标。

        在每个时间序列中，输入范围由随机时间位置 i1 和 i2 ，以及介于 0 和 1 之间的随机幅度 j1 和 j2 的 2 个峰值组成，目标范围由幅度 j2 - j1 和随机位置 i2 + ( i2 - i1) + randint(( 3, 3)。所有时间序列都被方差为 0.01 的加性高斯白噪声破坏。

 

•         ECG5000 (k = 56) 数据集

        来自 UCR 时间序列分类档案 [10]，由长度为 140 的 5000 个心电图 (ECG)（500 个用于训练，4500 个用于测试）组成。

        我们采用前 84 个时间步长（60 %）作为输入并预测每个时间序列的最后 56 个步骤（40%）（与 soft-dtw中的设置相同）。  

•         交通 (k = 24) 数据集

        对应于加州交通部（2015-2016 年的 48 个月）每 1 小时测量一次的道路占用率（0 到 1 之间）。

       

 4.1.2 网络架构和训练

        我们使用两种神经网络架构执行多步预测：

• 完全连接的网络（1 层 128 个神经元），不对数据结构做任何假设，
• Seq2Seq 模型 ， 带有门控循环单元（GRU），具有 1 层 128 个单元。

        每个模型都使用 PyTorch 训练最多 1000 个 epoch，并使用 ADAM 优化器进行 Early Stopping。

         DTW和TDI的平滑参数γ设置为0.01。 平衡 Lshape 和 Ltemporal 的超参数 α 在验证集上确定，以获得与 DTWγ 训练模型相当的 DTW 形状性能：对于 Synthetic 和 ECG5000，α = 0.5，对于 Traffic 为 0.8。

        我们实现 DILATE 的代码可从 https://github.com/vincent-leguen/DILATE 在线获得。

4.2 DILATE 效果

4.2.1 准确率比较

        我们评估 DILATE 的性能，并将其与两个强大的baseline进行比较：广泛使用的欧几里得 (MSE) 损失和 [13, 37] 中引入的平滑 DTW。

         对于每个实验，我们使用相同的神经网络架构（4.1.2），以进行公平比较。

        使用三个指标评估结果：MSE、DTW（形状）和 TDI（时间）。

        我们执行显着性水平为 0.05 的student- t 检验，以突出每个实验中的最佳方法（平均超过 10 次运行）。

        

         和以MSE作为损失函数的模型进行比较

在所有实验中对形状 (DTW) 进行评估时，DILATE 优于 MSE，在 5/6 实验中存在显着差异。

当按时间评估 (TDI) 时，DILATE 在所有实验中也表现更好（在 3/6 测试中存在显着差异）。

最后，在 3/6 实验中对 MSE 进行评估时，DILATE 等效于 MSE。

         DTWγ（soft-DTW）比较：

        在对形状 (DTWγ) 进行评估时，DILATE 的性能与 DTWγ 相似（2 个显着改进，1 个显着下降和 3 个等效性能）。

         对于时间 (TDI) 和 MSE 评估，DILATE 在所有实验中明显优于 DTWγ，正如预期的那样。

4.2.2 图像比较

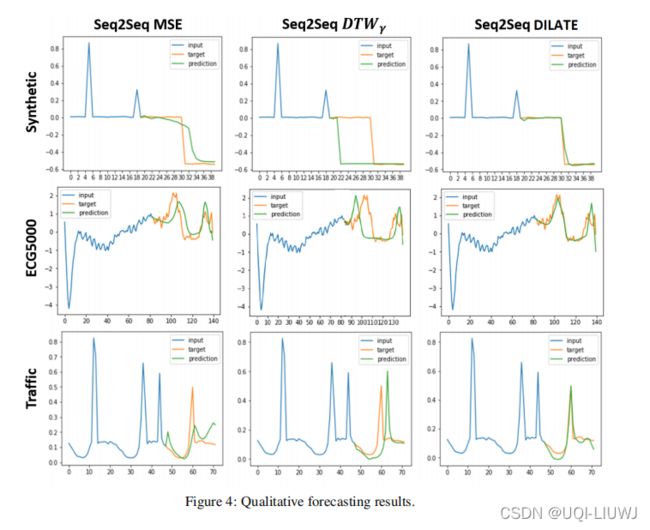
        我们在图 4 中展示了 Synthetic、ECG5000 和交通数据集的一些定性示例（其他示例在补充 2 中提供）。

         我们看到 MSE 训练导致预测不清晰，使得它们在出现下降或尖锐尖峰的情况下不足。

        DTWγ 会导致非常清晰的形状预测，但可能存在较大的时间错位。

        相比之下，我们的 DILATE 预测具有正确形状和精确时间定位的序列。  

 4.2.3 反向传播时间比较

        我们在图 5（a）中比较了标准 Pytorch 自动微分机制和我们自定义的反向传递实现（第 3.2 节）之间的计算时间。

        我们绘制了我们的实现相对于预测长度 k（平均超过 10 个随机目标/预测元组）的加速。（相比于pytorch 自动微分，加速了多少）

         我们注意到关于 k 的加速增加：提前 20 步预测的加速比为 × 20，提前 100 步预测的加速比最高为 × 35。

        

4.2.4 α的影响

        当 α = 1 时，减小为 DTWγ，形状良好但时间误差较大。

        当 α -→ 0 时，我们只最小化而没有任何形状约束。 在这种情况下，MSE 和形状误差都会爆炸，说明仅与 0一起才有意义。

                 

 4.2.5 和最新的时间序列模型的比较

        最后，我们将使用 DILATE 训练的 Seq2Seq 模型与使用 MSE 训练的两个最近用于时间序列预测的最先进的深度架构进行比较：

        LSTNet [30] 训练用于一步预测，我们递归地应用于多步（LSTNet -rec) ;

         Tensor-Train RNN (TT-RNN) [60] 为多步训练。

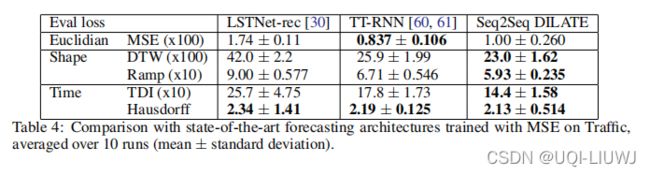
         表 4 中的交通数据集结果揭示了 TT-RNN 优于 LSTNet-rec 的优势，这表明专用的多步预测方法更适合这项任务。

        更重要的是，我们可以观察到我们的 Seq2Seq DILATE 在所有形状和时间指标上都优于 TT-RNN，尽管它在 MSE 上较差。 这突出了我们的 DILATE 损失函数的相关性，它可以通过更简单的架构达到更好的性能。

5 其他

        看到另一篇文章，形象地说明了MSE，soft-DTW和DILATE之间的区别:

时间序列预测损失函数 DTW, Soft-DTW, DILATE - 知乎 (zhihu.com)

        Soft-DTW 提供了一种可微的DTW算法，较之 Euclidian loss，其能使预测结果更好匹配实际情况的形状，但是Soft-DTW 并没有考虑预测的时延。

        比如说对于天气预报，正确的结果是1个小时后会有一场大暴雨。

• Euclidian loss(MSE) 预测告诉你1个小时后会有场雨，但是场中雨；
• Soft-DTW 预测告诉你未来会有场大暴雨，但会在2个小时之后来。对于时间要求更精确的预测场景，比如股价预测，虽然波动峰值形状预测对了，但是时间点预测错了，这对于买入/卖出操作来说会是一场灾难。

         基于这样的原因，Vincent Le Guen 等人在 Soft-DTW 的基础上提出了 DILATE（DIstortion Loss including shApe and TimE，时间与形状失真损失），同时考虑形状与时延。

        因为要考虑时延，因此用于对比的两个序列要一样长。