算法之图解单纯形算法C++

在之前的算法博客中，结合案例和算法的图形表示，获得了较多同学的好评，例如之前写的迪杰斯特拉算法这篇博客，能够让很多新同学和老同学通过直观的方式去理解算法求解的过程，这样理解起来会比较容易。最近关于求解线性规划的单纯形算法，在网络中目前没有发现比较好的图解该算法的博客，很多相关的博客可能会长篇大论，很多同学阅读的时候肯定很吃力，也很难坚持到最后，所以，想通过图形更直观的来讲一下单纯形算法。

1、线性规划问题介绍

线性规划问题是一个多变量线性函数的最优化问题，这些变量所满足的约束条件都是线性等式或者线性不等式。线性规划问题在我们的生活中非常常见，本文主要通过一个生活中的问题来讲解线性规划和单纯形算法。

1.1 问题：

有一个司机师父，他要给一家公司运输材料，运输的材料为水和特殊液体化学材料，其中，运输1立方水的利润为3块钱，运输1立方化学材料的利润为5块钱，但是，货车的最大容量为4立方，最大载重为6kg，其中，水的密度为1kg/立方，化学材质的密度为2kg/立方，那么，运输师父每次运输水和化学材料各多少立方时，总利润是最大的？

1.2 建立数学模型：

描述	符号表示
运输水的总体积	x
运输化学物质的总体积	y

根据运输的总利润，可以得到 总利润=3x+5y
根据货车体积限制，可以得到 x+y小于等于4
根据货车载重限制，可以得到 x+2y小于等于6
最基本的限制，货车运输两种物品的总体积为非负，即大于等于0

综上，我们可以建立下面的模型：

1.3 约束区域可视化

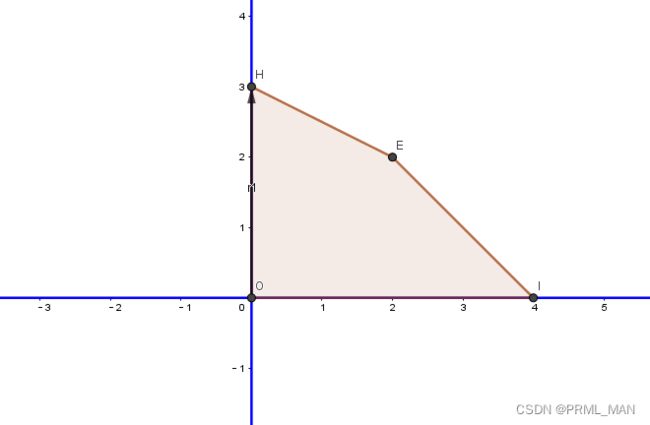
我们将线性规划问题区域通过图像绘制出来，同时将3x+5y=0的函数图像绘制出来，如下图：

2 图解单纯形算法

2.1 单纯形法约束条件：

	具体表述
条件1	目标函数必须是一个线性的最大化问题
条件2	所有的约束都必须是线性等式（除了非负约束）
条件3	所有的变量都必须要求是非负的

关于上面的模型，可以看出，第一条和第三条满足，不满足第二条，因此我们需要它能够给引入松弛变量 u,v将不等式变成等式：

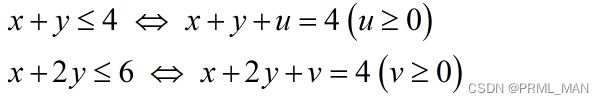
进而将模型转换成标准形式：

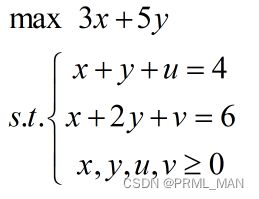
其中，标准形式的优势在于，可以通过简单的计算来确定可行区域的极点。

2.2 单纯形算法中的名词

表1 单纯形名词解释

名词	详细解释
基本可行解	如果一个基本解的所有坐标值都非负，则成为是一个基本可行解
单纯形表	来描述单纯形算法求解过程中系数和可行解的表
目标行	单纯形表的最后一行为目标行，前几列初始化为目标函数系数的相反数，最后一列为当前的目标函数值
输入变量	选择目标行中最小负数所在列对应的变量，即单位变化对目标函数影响最大的变量
主元列	输入变量所在的列称为主元列
分离变量	在将输入变量作为基变量的时候，需要将当前的一个基变量变为非基变量，该非基变量称为分离变量
θ比率	系数除以主元列中非零的值作为θ比率，θ比率越小的行对应的基变量作为本次的分离变量
主元行	分离变量对应的行作为主元行
主元化	将新的输入变量作为基变量的变换操作称为主元化，主要采用的变换方法跟线性方程组的高斯-若尔当消去法类似

2.3 单纯形算法求解线性规划

借助上面的模型，结合图像和单纯形算法的计算过程，来看一下如果求解线性规划问题。

1. 初始化，设模型有m个等式约束，n个变量（n>=m），将等式中 n-m个变量设置为0，求解其他变量的值，从而得到一个基本可行解，上面模型的n=4，m=2，假设x和y都为0，因此来求解 u,v 得到的基本可行解为（0，0，4，6）, 此时目标函数值为0，u,v为基变量，如下图中的O点。
   

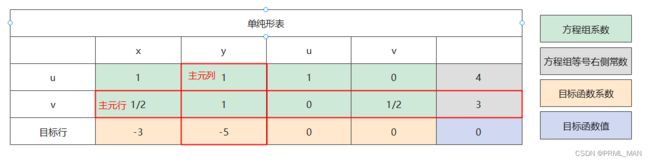
生成对应的单纯形表如下图，其中，绿色格代表方程组中各个变量的系数，灰色格表示方程组等号右侧的常数项，目标行中的黄色格初始化为目标函数对应变量系数的相反数，蓝色格代表目标函数当前的值：

2. 确定输入变量
   在上面表格中，0>-3>-5，因此选择-5所在列对应的变量为y，因此将y作为输入变量。 之所以这样选择，是因为该变量每个单位的增加能够使得目标函数获得最大的增大。 此时主元列如下图：

3. 确定分离变量
   分别求u和v的 θ比率值，下图中红色框的两列相除
   

计算结果如下：
θ(u) = 4/1 = 4
θ(v) = 6/2 = 3
θ(u) > θ(v)
因此，选择v为分离变量

4) 主元化
主元y代替分离变量v来作为新的基变量，这一步是单纯形算法中最复杂的一步，下面会详细介绍每一步的操作。
首先，将主元行的所有数除以主元行和主元列相交格中的数值，将主元列的系数变为1，计算过程如下图：



其次，对其他行的主元列进行消元，即将主元列的其他系数变成0

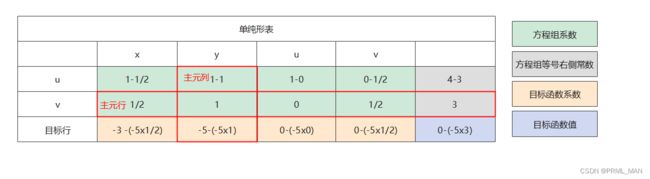
数据整理后得到下图，此时的目标值变为15：

在这个过程中，我们的目标函数具体是怎么变化了呢？我们通过图像直观的看一下目标函数的变化，如下图动画，首先，本次选择的主元列为y，此次目标函数所在位置为O点，从O点沿着y轴方向，建立了一个向量OH，沿着OH，进行移动，最终移动到极点H(0,3)上，此时的目标函数值为 3x+5y=30+53=15.

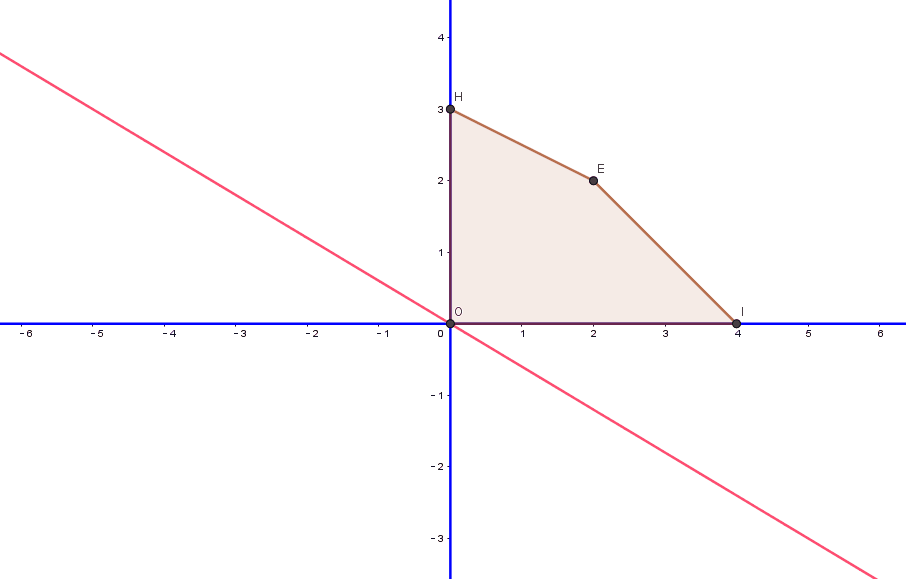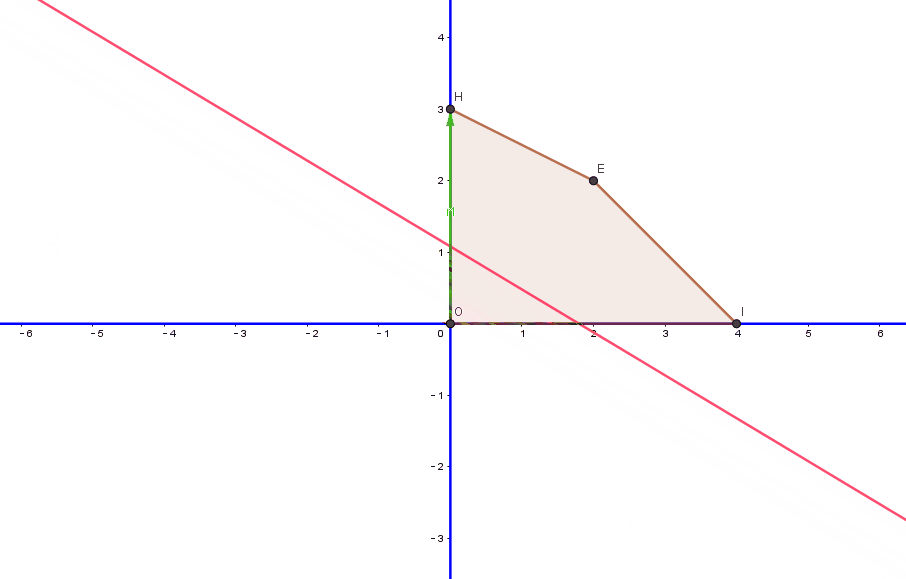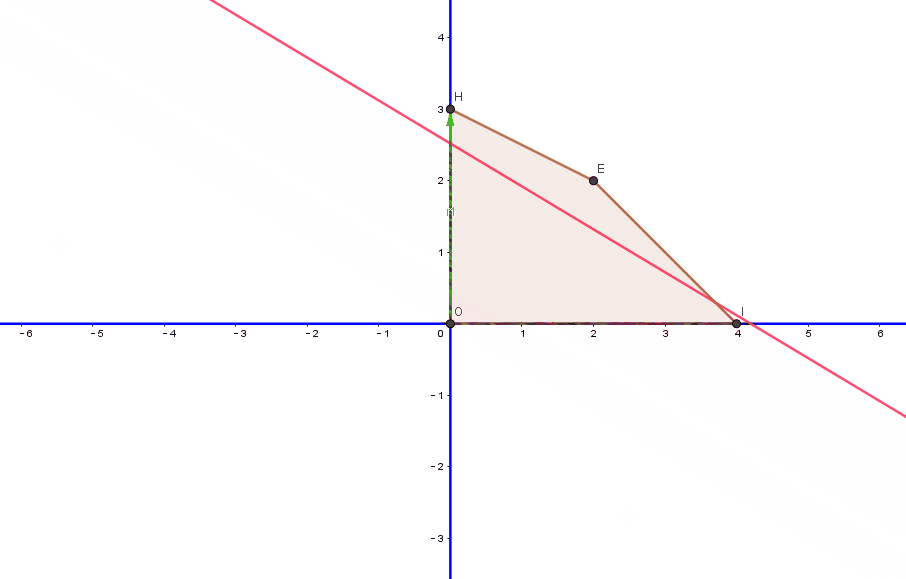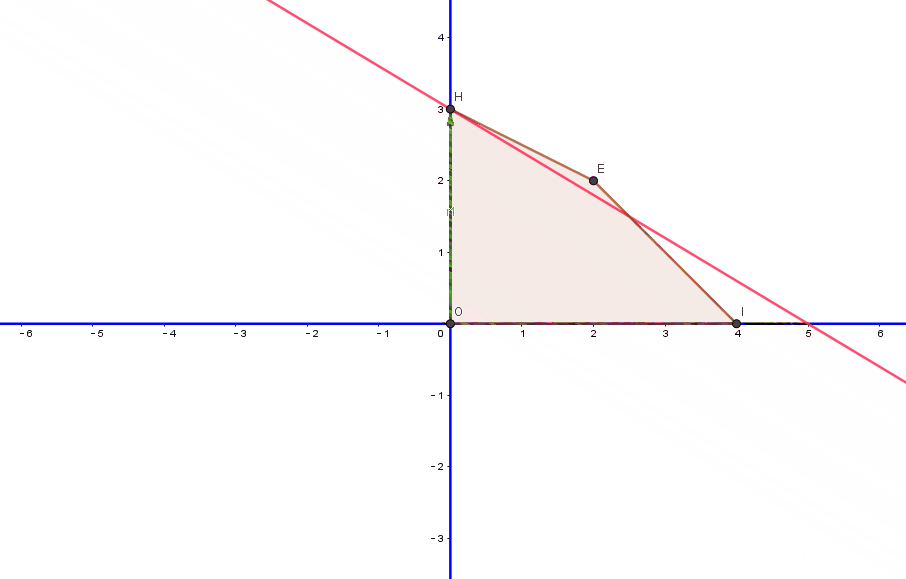
为什么是这样操作呢？因为经过上面的主元化操作，我们的基本解从（0,0,4,6） 变成了（0,3,1,0），关于xy的二维坐标系，就从（0,0）移动到（0,3）

5. 检查是否是最优解
   通过上面的动画图像，我们发现目前没有达到最优解，从单纯形表中发现，目标行中的系数值没有完全变成非负数，因此，还未求得最优解。为什么呢？因为只要有变量在目标行的系数非负，此时该变量还是有可以增加的空间的。

因此，我们再次运行步骤2到步骤4，新的输入变量变成x，求得输入变量为u ,主元化操作如下：

将主元行对应的主元系数变成1，如下图

列项消元得到下图：

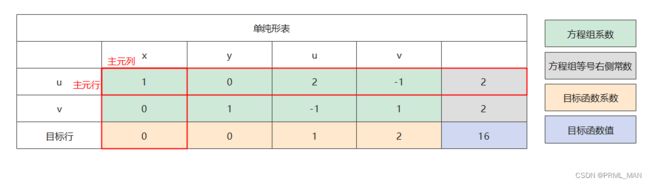
进行检查发现，目标行中的所有系数都变成非负数，此时达到了最优解，目标函数的最优值为16。此时求得的解为（2,2,0,0）,因此函数的解从（0,3,1,0）变为（2,2,0,0），我们通过图像来观察一下目标函数最优解的变化过程，如下面动画：

从上面的动画可以看出，单纯形算法一直从一个初始解，向最靠近目标函数最优解的极点靠近，每次迭代的解都是一个极点所对应的解。

3 单纯形算法回顾

经过上面的讲解，相信聪明的你应该对单纯形算法有了初步的理解，下面回顾一下整个算法的流程：

1 将模型变换成标准型
2 初始化：确定基变量，将非基变量设为0，求基本解，然后初始化单纯形表（基变量，变量系数，常数项列，目标行，目标函数值）中的五大变量
3 确定输入变量：通过目标行系数中的最小负数所在列对应的变量
4 确定分离变量：选取当前θ比率最小的基变量作为分离变量
5 检验最优：判断当前目标行的所有系数是否非负，如果有小于0，则继续回到步骤2-4，否则，达到最优，输出目标函数的最优值。

4 代码

时间有点晚，后面代码部分会找时间补上。