两阶段鲁棒优化 | Biilinear 项的线性化

两阶段鲁棒优化 | Biilinear 项的线性化

---

问题描述

假设两阶段鲁棒问题为：min-max-min，其中max-min为第二阶段问题。

在采用C&CG算法求解的时候，将第二阶段的max-min作为一个子问题。该问题不能直接进行求解，对其处理的方式一般有三种：
1. 启发式
2. KKT
3. 对内层进行对偶

启发式一般只能针对特殊的问题。绝大多数问题都可以采用KKT或者对偶的方法。

• 利用KKT条件转换时，问题必须满足extended relatively complete recourse assumption，即对于任意给定的第一阶段变量值，第二阶段子问题永远是 feasible and bounded 的。但采用KKT的时，reformulate后的式子中的互补松弛约束，一般都可以非常容易地采用大M法进行线性化。
• 对偶是一直可用的，但对偶之后存在bilinear的项。

翻了十几篇国内外的论文，对于此处bilinear的项，一般采用两种方式：

• 摆烂，直接求解器求
• 采用下面Gabrel¹ 的这个proposition

主要意思就是说，如果一个bilinear的问题有一个finite optimal value，那么bilinear项中变量的最优值分别在各自polyhedra的extreme point上（这部分线性规划的内容可以移步B站看方述诚老师的视频）。
据此，当$\Gamma$为一个整数的时候，$z_j$的最优解必定是0或1，而这个时候，bilinear的项就可以用大M法进行线性化了。（$\Gamma$为整数必须满足，否则极点不一定为0或1）

---

代码实现的时候踩的坑

向大佬请教了半天，结果发现是我自己没有搞清楚问题的本质。

原问题和线性化后的问题一定是相等的，即：
如果原问题是unbounded或者infeasible的，线性化后仍然一定是unbounded或者infeasible的

但我在代码实验的时候，发现当原问题unbounded的时候，线性化后的问题却有解

这里demo借用了运小筹公众号
鲁棒优化| C&CG算法求解两阶段鲁棒优化：全网最完整、最详细的【入门-完整推导-代码实现】笔记
中的一个例子。（入门两阶段鲁棒强烈推荐）

原问题(bilinear)代码如下：

from gurobipy import *
import numpy as np
K = 3
q = 2
""" The input parameter """
trans_cost = [[22, 33, 24],
            [33, 23, 30],
            [20, 25, 27]]
demand_nominal = [206, 274, 220]
demand_var = [40, 40, 40]
eposilon = 10e-6
""" build problem """
""" Create variables """
m = Model('master problem')
g_index = {}
pi_index = {}
theta_index ={}
d_index = {}
w_index = {}
for i in range(K):
    pi_index[i] = 0

for j in range(K):
    g_index[j] = 0
    d_index[j] = 0
    theta_index[j] = 0
    w_index[j] =0

m.setParam('NonConvex',2)
g = m.addVars(g_index.keys(), lb=0, ub=1, vtype=GRB.CONTINUOUS, name='g')
pi = m.addVars(pi_index.keys(), lb=-GRB.INFINITY, ub=0, vtype=GRB.CONTINUOUS, name='pi')
theta = m.addVars(theta_index.keys(), lb=-GRB.INFINITY, ub=0, vtype=GRB.CONTINUOUS, name='theta')
w = m.addVars(w_index.keys(), lb=0, ub=GRB.INFINITY, vtype=GRB.CONTINUOUS, name='w')


""" Set objective """
obj = LinExpr()
for i in range(K):
    obj.addTerms(q, pi[i])
obj2 = QuadExpr()
obj3 = LinExpr()
for j in range(K):
    obj2.addTerms(demand_var[j], g[j],theta[j])
    obj3.addTerms(demand_nominal[j],theta[j])
    # obj2.addTerms(1,d[j],theta[j])

m.setObjective(obj-obj2-obj3, GRB.MAXIMIZE)

""" Add Constraints """
# cons 1
for i in range(K):
    for j in range(K):
        m.addConstr(pi[i] - theta[j] <= trans_cost[i][j])
# for j in range(3):
#     m.addConstr(d[j] == demand_nominal[j] + g[j] * demand_var[j])

exp = LinExpr()
for j in range(K):
    exp.addTerms(1,g[j])
m.addConstr(g[j] <= 2)

m.optimize()
m.write('m.lp')

线性化(令$w_j=g_j{\theta }_j$，再用大M法)后的代码如下：

""" Set objective 2"""
obj = LinExpr()
for i in range(K):
    obj.addTerms(q, pi[i])
obj2 = LinExpr()
obj3 = LinExpr()
for j in range(K):
    obj2.addTerms(-demand_var[j], w[j])
    obj3.addTerms(demand_nominal[j],theta[j])
    # obj2.addTerms(1,d[j],theta[j])

m.setObjective(obj-obj2-obj3, GRB.MAXIMIZE)

""" Add Constraints """
# cons 1
for i in range(K):
    for j in range(K):
        m.addConstr(pi[i] - theta[j] <= trans_cost[i][j])
# for j in range(3):
#     m.addConstr(d[j] == demand_nominal[j] + g[j] * demand_var[j])

exp = LinExpr()
for j in range(K):
    exp.addTerms(1,g[j])
m.addConstr(g[j] <= 2)

M = 10e9
for j in range(K):
    m.addConstr(w[j] <= M * g[j])
    m.addConstr(w[j] <= -theta[j])
    m.addConstr(w[j] >= -theta[j] - M * (1 - g[j]))
m.optimize()
m.write('m2.lp')

结果跑完发现原问题unbounded，线性化之后却有最优解。

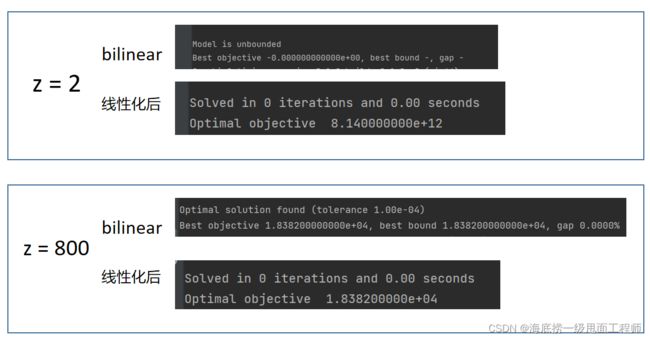
把代码来来回回重写检查了很多遍，开始怀疑线性化对原问题会有影响。However，理论经过了这么多代人的检验，一般是不会错的！最后问了师兄，提了句大M法，一针见血发现了问题就在这里：
大M的值取的太小了！ 导致线性化后的不等式不能按照你的想法来。

解决方法：

M = 10e9

改为

M = GRB.INFINITY

对线性化不太熟悉的可以看这里：
【教学视频】优化 | 线性化：两个0-1变量相乘的线性化
【教学视频】优化 | 线性化(2)：连续变量 * 0-1变量的线性化

---

1. Gabrel V, Lacroix M, Murat C, et al. Robust location transportation problems under uncertain demands[J]. Discrete Applied Mathematics, 2014, 164: 100-111. ↩︎