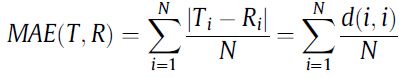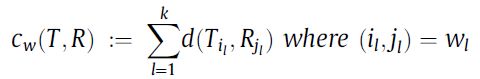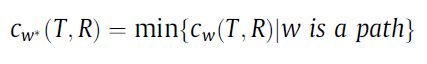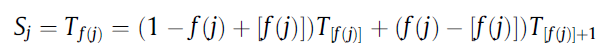时间序列预测之--时序误差处理（1）

DTW、TDI、DILATE

通过调整损失函数来处理时延问题，最早处理这种time difference问题的可以追溯到上个世纪70年代的Spoken Word Recognition的应用。在这种语音识别的问题中，时序问题是提高准确性的最重要的因素。我去看了一篇相应的文章，《Dynamic Programming Algorithm Optimization for Spoken Word Recognition》，也就是最原始的DTW。

但是基于这种Spoken Word Recognition应用，我还不理解整体的处理方式，我看完之后没法将文中提出的方案和文章研究的实际问题结合起来，理解不到位，所以先放着去看了别的应用。另一个在DILATE(NIPS2019)中提到的是TDI。

先回看一下DILATE中的temporal loss，这个temporal loss是基于TDI改变过来的，所以我又去看了TDI的相关文章，在一篇文章中，对TDI有着详细的描述。这篇文章也是用TDI来做能源预测的。

《Assessing energy forecasting inaccuracy by simultaneously considering temporal and absolute errors》

TDI的思想也是源于DTW。时序上的滞后其实是一种时序的畸变（temporal distortion），TDI是一种通过动态规划进行畸变的调整。如下图所示，正确地进行畸变的调整，可以改善误差。目前这篇文章我还没吃透，后面的理论有点复杂，我看到的这一部分TDI，应该是等预测结果出来之后才能进行调整。以下是实际效果。

但是在DILATE这篇文章中，将TDI改写到损失函数中，并不能提升曲线拟合的效果，看一下DILATE的结果：

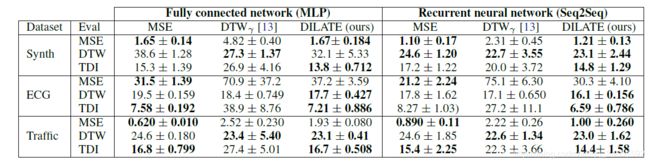
其实DILATE的temporal loss并没有改善MSE。

TDI算法

先是定义一下预测值和真实值，$T=(T_1,...,T_i,..,T_N),R=(R_1,...,R_j,..,R_N)$。

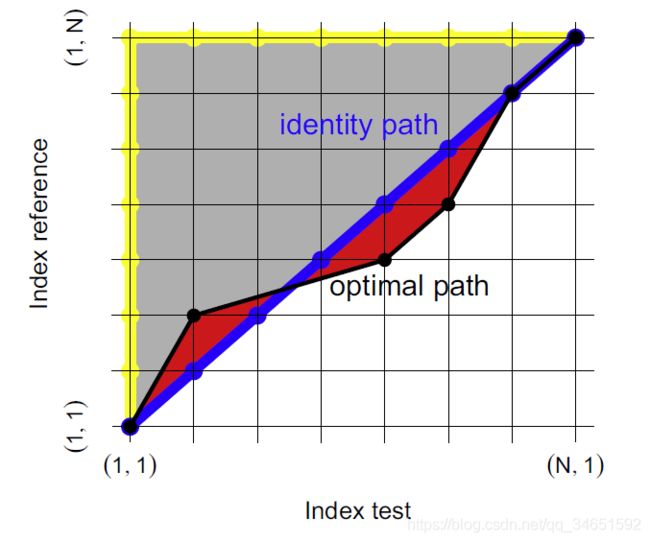
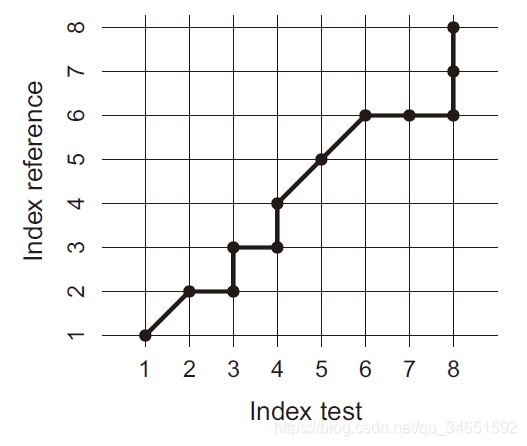
TDI大致的意思：比如下面这张图，横坐标是预测值的时间轴，纵坐标是真实值的时间轴。对应的 $i,j$ 分别是横纵坐标。网格上的每个点代表着，$T_i$与$R_j$是相关的，换句话说就是，$T_i$应该是 $j$ 时刻的预测值，只不过我们预测的时序发生了偏移。全部的相关点连起来就是一条路线，蓝线就是最理想的情况，每个时间点都没发生偏移。通过找到最优的匹配情况，将这些点连起来就成为一条最优路径。只要根据这条路径，做一些调整，就能修饰整体的曲线拟合情况。

以上是大概的流程，接下来看看具体情况。

1）代价定义

$d(T_i,R_j)=|T_i-R_j|$，简写为$d(i,j)$。两个序列间的MAE如下：

2）路径定义

路径=匹配，最优路径=最优匹配结果。$w=(w_1,...,w_l,...,w_k),w_l=(i_l,j_l)$。路径并不是随便取出来的，有以下几个约束：

• 边界约束：$w_1=(1,1),w_k=(N,N)$

• 单调性：$i_l-i_{l-1}\ge 0,j_l-j_{l-1}\ge 0$，这一点保证了最后能走到$(N,N)$。

• 连续性：$i_l-i_{l-1}\le 1,j_l-j_{l-1}\le 1$，这一点是为了保证不会出现非常大的跳跃，如果出现非常大的跳跃，就会导致调整过头。比如时刻1的值跟时刻100的值相等，但这个可能因为预测的原始值就是相等的。其实这是不可能得，预测不会偏差这么多，顶多在两三个时刻内有偏差。并且文中还提到，连续性的约束可以放宽，不一定非得局限在相邻时刻，可以是附近的三四个时刻之内。

  根据以上约束，大约能知道一个路径是什么样的，其实这样也存在一些问题，比如$R_2$与$T_2,T_3$都相关，就还是有点问题。

​
3）代价计算

​ 对于所有的可能路径而言，都计算一个代价，找出代价最小的路径，就是最优路径。

4）求解过程

动态规划求解最优路径。定义动态规划数组$D$,是一个N×N的数组。

每一个选项代表一种步进方式：

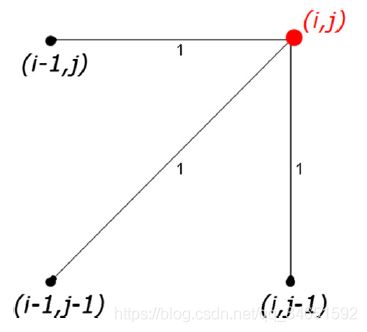
通过求取每一步的最小值，获得最后的最小值，获得这个最小值的路径就是最优路径。

5）序列调整

​ 调整主要使用插值函数进行调整。