配电网可靠性评估（一）—最小路法和非序贯蒙特卡洛模拟法的matlab实现

---

一、简介

电力系统的可靠性研究是相关领域的热点问题。根据研究对象的不同，又可分为发电系统的可靠性，输电系统的可靠性和配电系统的可靠性。配电网在电力系统中处于最末端的位置，直接和用户相连，一旦出现故障情况，就会在用户侧表现为停电事故。因此对配电网的可靠性评估有着重大意义。

---

一、可靠性评估的主要指标

1.负荷可靠性指标

1.1故障率$\lambda$

表示负荷在单位时间内因元件故障而发生停电事故的频率，单位为（次/年），计算公式为：$$\lambda =\sum _{i\in D}{\lambda }_i$$
式中，$D$表示会影响该负荷的元件集合，${\lambda }_i$表示第$i$个元件的故障率。

1.2停电持续时间$\gamma$

表示负荷每次发生停电事故的平均持续时间，单位为（小时/次），计算公式为：$$\gamma =\frac{{\sum }_{i\in D}{\lambda }_i{\gamma }_i}{{\sum }_{i\in D}{\lambda }_i}$$
式中，${\gamma }_i$表示第$i$个元件的平均故障时间。

1.3年平均停电时间$U$

表示负荷在一年内停电的平均时间，单位为（小时/年），计算公式为：$$U=\gamma \lambda$$

2.系统可靠性指标

2.1系统平均停电频率$SAIFI$

表示在该系统中每个用户在一年内的平均停电次数，单位是（次/（户·年））。

2.2系统平均停电时间$SAIDI$

表示在该系统中每个用户在一年内的平均停电时间，单位是（小时/（户·年））。

2.3供电可靠率$ASAI$

表示单位时间内用户有效供电小时数与总时间的比值。

二、可靠性评估方法

1.解析法

解析法，顾名思义就是用能解析的方法求解可靠性。一般都是是通过列举分析所有的系统故障状态来计算可靠性指标，主要有故障模式后果分析法、网络等值法、故障扩散法、最小路法等。这里主要介绍最小路算法：

应用最小路算法时，首先可以求出每个负荷与电源之间的最短路径，也就是负荷的最小路。那么对这个负荷来说，整个配电网上的元件就可以分成最小路上的元件和非最小路上的元件。在最小路上的元件，故障时都会对负荷造成影响；对于非最小路上的元件，可以根据该元件所处的位置，保护配置等判断是否对负荷有影响，最终求出负荷的可靠性指标，再由负荷的可靠性指标便可以求出系统的可靠性指标。以下面简单的配电网为例：

对于负荷1来说，最小路上的元件包括断路器QF1、线路1和线路2、熔断器FU1、变压器T1，其中每一个元件停运，都会引起负荷停运，引起负荷的停运时间就是元件的故障恢复时间。非最小路上的元件包括线路3-8，变压器2-4，其中线路4和线路8、变压器2和4存在熔断器保护，因此故障时不会影响负荷1。剩余的元件中，线路3和线路5故障时，断路器QF1动作影响负荷1供电，且引起负荷的停运时间为元件的故障恢复时间；线路6、线路7和变压器3故障时分段开关S会动作，理论上开关动作时负荷1会短暂停电，引起负荷1停电时间就是开关的动作时间。

其余节点的分析和对负荷1的分析完全相同。

算例采用IEEE RBTS BUS6系统，非常经典的配电网可靠性测试系统，数据很全也比较好找：

数据文件如下：

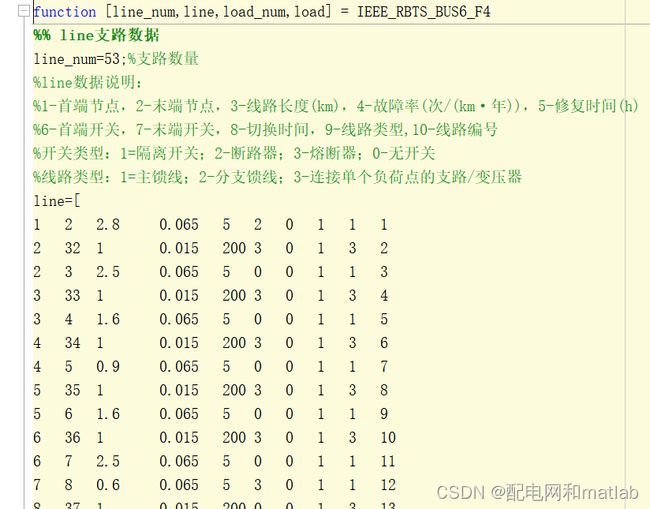
采用matlab编程，应用最小路法求负荷以及系统的可靠性：

clc;clear;
tic
%读取数据
[line_num,line,load_num,load] = IEEE_RBTS_BUS6_F4;
%初始化负荷点可靠性指标
Lambda_load=zeros(1,load_num);
Gamma_load=zeros(1,load_num);
load_users=zeros(1,load_num);
%求每个负荷的可靠性参数
for i=1:load_num
	省略……
end
SAIFI=Lambda_load*(load_users')/(sum(load_users))
SAIDI=U_load*(load_users')/(sum(load_users))
CAIDI=SAIDI/SAIFI
ASAI=1-SAIDI/8760

运行结果如下：

2.模拟法

模拟法就是指蒙特卡洛模拟法。在进行供电可靠性评估时，通过随机抽样获取系统的状态，再结合统计学的方法得到可靠性指标的估计值。解析法求解的可靠性指标是精确值，但模拟法通过仿真求解，得到的结果并不是完全精确的，结果的精确度和抽样次数有很大的关系。蒙特卡洛模拟法又可以分为序贯蒙特卡洛模拟法和非序贯蒙特卡洛模拟法。下面重点介绍非序贯蒙特卡洛模拟法。

非序贯蒙特卡洛模拟法基本原理如下：

首先假设配电系统中的每个元件都存在故障和正常运行两种状态，且每个元件的状态是相互独立的；然后用$s_i$表示第$i$个元件的状态，且该元件故障率为${\lambda }_i$，平均修复时间为${\gamma }_i$；最后，对该元件产生一个在$[0,1]$之间均匀分布的随机数$E_i$，如果$E_i$在$[0,{\lambda }_i]$之间，表示该元件发生故障，否则可以认为元件处于正常工作状态。

元件保持在正常状态的时间记为正常运行时间TTF，元件故障的时间记为修复时间TTR，分段开关切换时间记为开关切换时间TTS，可以近似认为元件的故障修复时间服从指数分布，求出TTF、TTR和TTS。

那么求解的具体步骤就是：首先确定系统中每个元件的状态，再由故障元件确定受影响的负荷和负荷的停运时间，这样一次就完成了一次系统状态抽样的过程，重复多次便可以得到负荷的停电频率和停电持续时间，再进一步求得系统的可靠性指标。
matlab代码如下：

clc;clear;
%读取数据
[line_num,line,load_num,load] = IEEE_RBTS_BUS6_F4;
%生成图
g=digraph(line(:,1),line(:,2),line(:,3));
%初始化影响矩阵
equipment_load=zeros(line_num,load_num);
operator_load=zeros(line_num,load_num);
%利用节点网络分析法确定影响负荷的元件
tic
for i=1:load_num
	省略……
end
load_fault=zeros(1,load_num);%故障次数
load_fault_time=zeros(1,load_num);%故障时间
Lambda=zeros(1,line_num);
Gamma1=zeros(1,line_num);
Gamma2=zeros(1,line_num);
%非序贯蒙特卡洛模拟法
N=1000000;%仿真次数
for i=1:N
	省略……
end
Lambda_load=load_fault/N;
U_load=load_fault_time/N;
Gamma_load=U_load./Lambda_load;
SAIFI=Lambda_load*(load_users')/(sum(load_users))
SAIDI=U_load*(load_users')/(sum(load_users))
CAIDI=U_load*(load_users')/(Lambda_load*(load_users'))
ASAI=1-U_load*(load_users')/(sum(load_users*8760))

运行结果如下：



如果运行过的代码的朋友可以发现，解析法每次求出来的结果是不变的，而模拟法的结果是一直都在变化。所以还需要分析一下模拟法的误差。从下面的图可以看到，在仿真次数取一百万次时，结果还是比较精确的，和精确值的误差数量级在$10^{-3}$。

PS:完整程序见链接：

基于最小路法\蒙特卡洛法的配电网可靠性评估