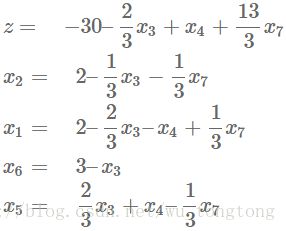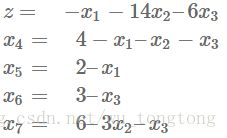线性规划之二 —— 单纯形算法（详解）

鸣谢dalao的教导

单纯形算法是求解线性规划的经典方法
虽然ta的执行时间在最坏的情况下并不是多项式，然而在实际中这个算法通常是相当快速的

实际上也非常简单，主要就三个步骤：

• 找到一个初始的基本可行解
• 不断的进行旋转（PIVOT）操作
• 重复第二步直到结果不能改进为止

单纯形算法的一个例子

考虑下面这个标准型的线性规划：
最小化：
−x1−14x2−6x3 − x 1 − 14 x 2 − 6 x 3
满足约束：
x1+x2+x3<=4 x 1 + x 2 + x 3 <= 4
x1<=2 x 1 <= 2
x3<=3 x 3 <= 3
3x2+x3<=6 3 x 2 + x 3 <= 6
x1,x2,x3>=0 x 1 , x 2 , x 3 >= 0

为了使用单纯形算法，我们必须将此线性规划转换成松弛型：
min
−x1−14x2−6x3 − x 1 − 14 x 2 − 6 x 3
s.t.
x1+x2+x3+x4=4 x 1 + x 2 + x 3 + x 4 = 4

x1+x5=2 x 1 + x 5 = 2

x3+x6=3 x 3 + x 6 = 3

3x2+x3+x7=6 3 x 2 + x 3 + x 7 = 6

x1,x2,x3,x4,x5,x6,x7>=0 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 >= 0

移一下项：
z=−x1−14x2−6x3 z = − x 1 − 14 x 2 − 6 x 3

x4=4−x1−x2−x3 x 4 = 4 − x 1 − x 2 − x 3

x5=2−x1 x 5 = 2 − x 1

x6=3−x3 x 6 = 3 − x 3

x7=6−3x2−x3 x 7 = 6 − 3 x 2 − x 3

x1,x2,x3,x4,x5,x6,x7>=0 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 >= 0

在上述的等式的左边称为基本变量，而右边称为非基本变量

单纯形算法的第一步就是构造一个基本解
我们直接用最简单的方法：
把等式右边的非基本变量设为0，计算出左边基本变量的值
容易得到基本解为： (x1,x2….x7)=(0,0,0,4,2,3,6) ( x 1 , x 2 … . x 7 ) = ( 0 , 0 , 0 , 4 , 2 , 3 , 6 ) ，而目标值z = 0，其实就是把基本变量 xi x i 设置为 bi b i

一般而言，基本解是可行的，我们称其为基本可行解
初始的基本解不可行的情况见后面的讨论
这里假设初始的基本解就是基本可行解，因此三个步骤中第一步完成了

现在我们就可以开始第二个步骤了：
我们每次选择一个在目标函数中的系数为负的非基本变量 xe x e
然后尽可能的增加 xe x e 而不违反约束

并将 xe x e 用基本变量 xl x l 表示， 然后把 xe x e 变为基本变量， xl x l 变为非基本变量

这里，假设我们选择增加 x1 x 1 ，那么在上述的等式（不包括目标函数 z z 那行）中，
第1 1 个等式限制了 x1<=4 x 1 <= 4 （因为 x4>=0 x 4 >= 0 ）
第 2 2 个等式有最严格的限制，它限制了x1<=2 x 1 <= 2
因此我们最多只能将 x1 x 1 增加到 2 2
根据上面的第二个等式，我们有：x1=2–x5 x 1 = 2 – x 5 ，带入上面所有的等式就实现了 xe x e 和 xl x l 的替换：

z=−2+x5−14x2−6x3 z = − 2 + x 5 − 14 x 2 − 6 x 3

x4=2+x5−x2−x3 x 4 = 2 + x 5 − x 2 − x 3

x1=2−x5 x 1 = 2 − x 5

x6=3−x3 x 6 = 3 − x 3

x7=6−3x2−x3 x 7 = 6 − 3 x 2 − x 3

x1,x2,x3,x4,x5,x6,x7>=0 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 >= 0

实际上这就是一个转动的过程，一次转动选取一个非基本变量（也叫替入变量） xe x e 和一个基本变量（也叫替出变量） xl x l ，然后替换二者的角色
执行一次转动的过程与之前所描述的线性规划是等价的

同样的，我们将非基本变量设为0，于是得到： (x1,x2,...,x7)=(2,0,0,2,0,3,6),z=−2 ( x 1 , x 2 , . . . , x 7 ) = ( 2 , 0 , 0 , 2 , 0 , 3 , 6 ) , z = − 2
说明我们的目标减少了 −2 − 2

接下来是单纯形算法的第三步，就是不断地进行转动，直到无法进行改进为止，那我们就继续进行刚才的例子：

我们接着再执行一个转动，这次我们可以选择增大 x2 x 2 或 x3 x 3 ，
但是我们不能选择 x5 x 5 ，因为增大 x5 x 5 之后 z z 也增大，而我们要求最小化z z

那我们就选择 x2 x 2 吧：
从条件中可以看出， x2 x 2 最多能够增加到2

z=−30+8x3+14x4−13x5 z = − 30 + 8 x 3 + 14 x 4 − 13 x 5

x2=2+x5−x4−x3 x 2 = 2 + x 5 − x 4 − x 3

x1=2−x5 x 1 = 2 − x 5

x6=3−x3 x 6 = 3 − x 3

x7=2x3+3x4−3x5 x 7 = 2 x 3 + 3 x 4 − 3 x 5

此时，我们的基本解变为 (x1,x2….x7)=(2,2,0,0,0,3,0)，z=−30 ( x 1 , x 2 … . x 7 ) = ( 2 , 2 , 0 , 0 , 0 , 3 , 0 ) ， z = − 30

我们可以继续的选择增大 x5 x 5 （只能选择系数是负的），第4个等式具有最严格的限制（ 0–3x5>=0 0 – 3 x 5 >= 0 ），我们有 x5=2/3∗x3+x4–1/3∗x7 x 5 = 2 / 3 ∗ x 3 + x 4 – 1 / 3 ∗ x 7

此时，我们的基本解变为 (x1,x2….x7)=(2,2,0,0,0,3,0)，z=−30 ( x 1 , x 2 … . x 7 ) = ( 2 , 2 , 0 , 0 , 0 , 3 , 0 ) ， z = − 30 ，这时候并没有增加
但是这并不是最大值，我们还要继续旋转

这一次我们选择增加 x3 x 3
第2个和第3个有最严格的限制，我们选第2个的话，得： x3=3–3/2∗x1–3/2∗x4+1/2∗x7 x 3 = 3 – 3 / 2 ∗ x 1 – 3 / 2 ∗ x 4 + 1 / 2 ∗ x 7

现在我们好像已经没有可以旋转的值了，算法停止
z=−32 z = − 32 就是我们的解
而此时，基本解为： (x1,x2….x7)=(0,1,3,0,2,0,0) ( x 1 , x 2 … . x 7 ) = ( 0 , 1 , 3 , 0 , 2 , 0 , 0 ) ，看看最开始的目标函数： z=−x1−14x2–6x3 z = − x 1 − 14 x 2 – 6 x 3
我们将 x2=1,x3=3 x 2 = 1 , x 3 = 3 带入得， z=−32 z = − 32 ，说明我们经过一系列的旋转后，得到了目标值

退化

在刚才的例子中，有两次旋转的目标值是一样的，这种现象称为退化

退化可能会导致循环（cycling）的情况，这是使得单纯形算法不会终止的唯一原因
还好上面的例子中，我们没有产生循环的情况，再次旋转，目标值继续降低

如何避免退化？一个方法就是使用 Bland B l a n d 规则：

在选择替入变量和替出变量的时候，我们总是选择满足条件的下标最小值

替入变量 xe x e ：目标条件中，系数为负数的第一个作为替入变量
替出变量 xl x l ：对所有的约束条件中，选择对 xe x e 约束最紧的第一个

在上面的例子中，我们就是这么做的

（另一个方法是加入随机扰动）

无界(unbounded)情况

最小化：
−x1−x2 − x 1 − x 2
约束条件：
x1−x2<=1 x 1 − x 2 <= 1
−x1+x2<=1 − x 1 + x 2 <= 1
x1,x2>=0 x 1 , x 2 >= 0

那这个例子用松弛型怎么表示呢？

z=−x1−x2 z = − x 1 − x 2
x1−x2+x3=1 x 1 − x 2 + x 3 = 1
−x1+x2+x4=1 − x 1 + x 2 + x 4 = 1
x1,x2>=0 x 1 , x 2 >= 0

z=−x1−x2 z = − x 1 − x 2
x3=1−x1+x2 x 3 = 1 − x 1 + x 2
x4=1+x1−x2 x 4 = 1 + x 1 − x 2
x1,x2,x3,x4>=0 x 1 , x 2 , x 3 , x 4 >= 0

选取替入变量 x1 x 1
z=−1−2x2+x3 z = − 1 − 2 x 2 + x 3
x1=1+x2−x3 x 1 = 1 + x 2 − x 3
x4=2−x3 x 4 = 2 − x 3
x1,x2,x3,x4>=0 x 1 , x 2 , x 3 , x 4 >= 0

这时候我们只能选择 x2 x 2 为替入变量，才能使得目标值变小，
但是我们发现，对于 x2 x 2 没有任何的约束，也就是说， x2 x 2 可以无限大，所以这是没有边界的情况

这个情况是我们有一个替入变量，但是找不到一个替出变量导致的，
这时候就是无界的情况了，写算法的时候注意判断一下即可

具体实现

我们回到一开始的例子：

min
z=−x1−14x2−6x3 z = − x 1 − 14 x 2 − 6 x 3
s.t.
x1+x2+x3+x4=4 x 1 + x 2 + x 3 + x 4 = 4

x1+x5=2 x 1 + x 5 = 2

x3+x6=3 x 3 + x 6 = 3

3x2+x3+x7=6 3 x 2 + x 3 + x 7 = 6

x1,x2,x3,x4,x5,x6,x7>=0 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 >= 0

我们得到下面的矩阵：

• 矩阵A：约束条件的系数（等号左边的系数）
• 矩阵B：约束条件的值（等号右边）
• 矩阵C：目标函数的系数值

我们将ta们拼接起来：

可以注意到最左上角多出来一个0，那是什么呢？

这个是 −z − z ，初始时 −z=0 − z = 0

将上面那个矩阵和写成基本变量 = 非基本变量的形式对比：

可以发现，非基本变量符号都与原先的相反，基本变量符号相同

接着以进行第二步吧，
来看看我们的矩阵是如何进行运算的，第二步我们的结果如下（我们选择了 x1 x 1 为替入变量， x5 x 5 为替出变量）：

z=−2−14x2−6x3+x5 z = − 2 − 14 x 2 − 6 x 3 + x 5
x4=2−x2−x3+x5 x 4 = 2 − x 2 − x 3 + x 5
x1=2−x5 x 1 = 2 − x 5
x6=3−x3 x 6 = 3 − x 3
x7=6−3x2−x3 x 7 = 6 − 3 x 2 − x 3

我们选择的式子是x第二个
首先看看约束条件的式子， x1=2–x5 x 1 = 2 – x 5
我们改写成： 2=x1+x5 2 = x 1 + x 5
因此第二个式子对应的矩阵就是： (2,1,0,0,0,1,0,0) ( 2 , 1 , 0 , 0 , 0 , 1 , 0 , 0 )
其它的类推，注意-z，因此我们的矩阵应该是如下形式的：

那么 S1 S 1 是怎么变成 S2 S 2 的呢?

首先是第2行，我们是将 x1 x 1 用 x5 x 5 表示 (x1=x5) ( x 1 = x 5 )
在等式的变换中，就是移项，然后每一个都除以 x1 x 1 的系数
其实用矩阵很简单，这里就是mat[2] /= mat[2][1] ，表示矩阵第二行都除以第二行第一个元素

其它行呢？

只要有 x1 x 1 的，我们都用 x1=2–x5 x 1 = 2 – x 5 来表示，
就是减去该行 x1 x 1 的系数 ∗mat[2] ∗ m a t [ 2 ]
mat[i]=mat[i]–mat[2]∗mat[i][1] m a t [ i ] = m a t [ i ] – m a t [ 2 ] ∗ m a t [ i ] [ 1 ]
这样就实现了约束条件中替入和替出变量的替换

对于目标函数

将 x1 x 1 用 2–x5 2 – x 5 来表示，参照上面的思路，同样的减法： mat[0]=mat[0]–mat[2]∗(C中x1的系数)=mat[0]+mat[2] m a t [ 0 ] = m a t [ 0 ] – m a t [ 2 ] ∗ ( C 中 x 1 的 系 数 ) = m a t [ 0 ] + m a t [ 2 ]
注意到其实我们的 z=−2 z = − 2 ，而左上角的为 2 2 ，也就是−z − z ，这就是我们为啥说左上角是 −z − z 的原因

简单总结一下：

• 首先我们从目标函数中找到一个系数不为0的变量，确定ta为替入变量 e e
• 在所有的约束条件中，找到最苛刻的约束条件l l
• 修改矩阵
  
  • 当前行（变量系数和常数）：该行除以 e e 的系数
    A[l][i]=A[l][i]/A[l][e],A[l][e]=1/A[l][e] A [ l ] [ i ] = A [ l ] [ i ] / A [ l ] [ e ] , A [ l ] [ e ] = 1 / A [ l ] [ e ]
  • 其他行（变量系数和常数）：该行减去该行 e e 的系数∗l ∗ l 行
    A[i][j]=A[i][j]−A[i][e]∗A[l][j],A[i][e]=−A[i][e]∗A[l][e] A [ i ] [ j ] = A [ i ] [ j ] − A [ i ] [ e ] ∗ A [ l ] [ j ] , A [ i ] [ e ] = − A [ i ] [ e ] ∗ A [ l ] [ e ]
  • 目标函数：该行减去 C C 中 e e 的系数 ∗l ∗ l 行
    C[i]=C[i]−C[e]∗A[l][i],C[e]=−C[e]∗A[l][e] C [ i ] = C [ i ] − C [ e ] ∗ A [ l ] [ i ] , C [ e ] = − C [ e ] ∗ A [ l ] [ e ]

初始解 ≠ 基本可行解||无解

我们在一开始例子引入的时候，我们有一个很重要的前提：

初始解是基本可行解

但是有例外，怎么破？

先来个例子（例一）：
min：
x1+2x2 x 1 + 2 x 2
s.t.：
x1+x2<=2 x 1 + x 2 <= 2
x1+x2>=1 x 1 + x 2 >= 1
x1,x2>=0 x 1 , x 2 >= 0

min：
x1+2x2 x 1 + 2 x 2
s.t.：
x1+x2<=2 x 1 + x 2 <= 2
−x1−x2<=−1 − x 1 − x 2 <= − 1
x1,x2>=0 x 1 , x 2 >= 0

z=x1+2x2 z = x 1 + 2 x 2
x1+x2+x3=2 x 1 + x 2 + x 3 = 2
−x1−x2+x4=−1 − x 1 − x 2 + x 4 = − 1
x1,x2,x3,x4>=0 x 1 , x 2 , x 3 , x 4 >= 0

z=x1+2x2 z = x 1 + 2 x 2
x3=2−x1−x2 x 3 = 2 − x 1 − x 2
x4=−1+x1+x2 x 4 = − 1 + x 1 + x 2
x1,x2,x3,x4>=0 x 1 , x 2 , x 3 , x 4 >= 0

我们像之前一样得到一个初始解： (x1,x2,x3,x4)=(0,0,2,−1) ( x 1 , x 2 , x 3 , x 4 ) = ( 0 , 0 , 2 , − 1 )
但是 x4=−1 x 4 = − 1 是不满足条件的，即初始解不是基本可行解

那么再来一个例子（例二）：
min：
x1+2x2 x 1 + 2 x 2
s.t.：
x1+x2>=2 x 1 + x 2 >= 2
x1+x2<=1 x 1 + x 2 <= 1
x1,x2>=0 x 1 , x 2 >= 0

从前两个式子就可以看出来，这个线性规划是无解的

我们来看看初始解的情况：
z=x1+2x2 z = x 1 + 2 x 2
x3=−2+x1+x2 x 3 = − 2 + x 1 + x 2
x4=1−x1−x2 x 4 = 1 − x 1 − x 2
x1,x2,x3,x4>=0 x 1 , x 2 , x 3 , x 4 >= 0

有： (x1,x2,x3,x4)=(0,0,−2,1) ( x 1 , x 2 , x 3 , x 4 ) = ( 0 , 0 , − 2 , 1 ) ，但是 x3=−2 x 3 = − 2 是不满足条件的，即初始解不是基本可行解

最大值<=>最小值

之前我们的不等式都是这个形式： x1+x2<=z x 1 + x 2 <= z ，求解目标函数的最大值
但是如果我们遇到 x1+x2>=z x 1 + x 2 >= z ，求解目标函数的最小值，这要怎么办呢

这种情况下，我们就需要一个很厉害的定理：对偶定理

简单来说，就是：
如果原线性规划的目标函数是最大值，我们可以通过转化，使其变成求取最小值的目标函数
两个线性规划的目标函数最优值相等

如果目标函数的系数构成的矩阵为 C C ——它是一个行向量
约束条件的常数构成的矩阵为B B ——它是一个列向量
约束条件中所有的系数构成的矩阵为 A A

那么我们把A A 的 I,J I , J 转置，再把 B B 和C C 交换，把求最大值变成求最小值（或把求最小值变成求最大值）
就得到了一个新的线性规划
ta和原来的线性规划的基变量个数可能是不同的，但最优解是相同的

举个例子，
对于线性规划： Maximize−Cx(S.T.Ax<=B,x>=0) M a x i m i z e − C x ( S . T . A x <= B , x >= 0 )
我们可以把它转化成等价的线性规划： Minmize−BTx(S.T.ATy<=CT,y>=0) M i n m i z e − B T x ( S . T . A T y <= C T , y >= 0 )

SEE THE CODE

//最大值 

#include
#include
#include

using namespace std;

const double eps=1e-7;
const double INF=1e10;
int n,m; 
double a[10003][1003],b[10003],c[10010],ans,v;
//a:约束条件的系数
//b:约束条件的常数
//c:目标函数的系数

void priov(int l,int e)
{
    b[l]/=a[l][e];
    for (int i=1;i<=m;i++)            //l行中的每一元素都除以e的系数 
        if (i!=e) a[l][i]/=a[l][e];
    a[l][e]=1/a[l][e];
    for (int i=1;i<=n;i++)
        if (i!=l&&fabs(a[i][e])>eps)  //有e这个变量的行 
        {
            b[i]-=b[l]*a[i][e];
            for (int j=1;j<=m;j++)
                if (j!=e) a[i][j]-=a[l][j]*a[i][e];
            a[i][e]=-a[i][e]*a[l][e];
        }
    v+=c[e]*b[l];
    for (int i=1;i<=m;i++)
        if (i!=e) c[i]-=c[e]*a[l][i];
    c[e]=-c[e]*a[l][e];
}

double simple()
{
    int l,i,e;
    double t;
    v=0.0;
    while (1)
    {
        for (i=1;i<=m;i++)
            if (c[i]>eps) break;
        e=i;    //系数不为零的一项 替入变量 
        if (e==m+1) return v;
        t=INF; 
        for (i=1;i<=n;i++)
            if ((a[i][e]>eps)&&(t>b[i]/a[i][e]))
               t=b[i]/a[i][e],l=i;   
        if (t==INF) return INF;    //无界状态 
        priov(l,e);   //l 替入变量限制最紧的一行 
    }
}

int main()
{
    scanf("%d%d",&m,&n);
    for (int i=1;i<=m;i++)
        scanf("%lf",&c[i]);
    for (int i=1;i<=n;i++)
    {
        int l,r;
        scanf("%d%d%lf",&l,&r,&b[i]);
        for (int j=l;j<=r;j++)
            a[i][j]++;
    }
    ans=simple();
    printf("%.0lf",ans);
    return 0;
}