人工智能系列实验(四)——多种神经网络参数初始化方法对比(Xavier初始化和He初始化)
本实验利用Python,搭建了一个用于区分不同颜色区域的浅层神经网络。通过使用三种不同的初始化方法:全0初始化、随机初始化和He初始化,比较改变初始化方法对最终预测效果的影响。
实验原理:
为什么要初始化权重
权重初始化的目的是防止在深度神经网络的正向传播过程中层激活函数的输出损失梯度出现爆炸或消失。如果发生任何一种情况,损失梯度太大或太小,就无法有效地向后传播,并且即便可以向后传播,网络也需要花更长时间来达到收敛。
全0初始化
全0初始化是最差的初始化方法,只适用于单神经元神经网络,如人工智能系列实验(一)——用于识别猫的二分类单层神经网络。对于任何具有隐藏层的神经网络,如果初始化时所有的权重都是相同的,则任意一层多神经元的效果都与单神经元相同,无法对多特征进行学习,白白浪费计算力。
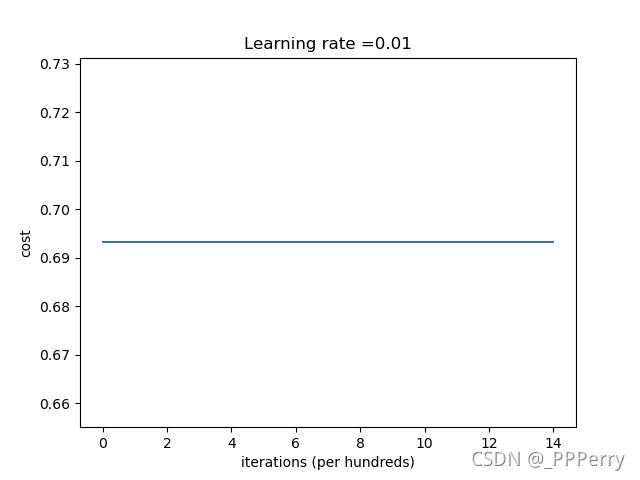
而全0初始化又是相同权重初始化的一种特殊情况,根据反向传播的链式法则,具有隐藏层的神经网络参数将永远不会更新,cost函数永远不会下降。
随机初始化
随机初始化是最常见的一种初始化方法:W参数全部随机初始化,b参数全部初始化为0。
在python中,使用np.random.randn和np.zeros函数初始化即可。
Xavier初始化
条件:正向传播时,激活值的方差保持不变;反向传播时,关于状态值的梯度的方差保持不变。其中,激活值是激活函数输出的值,状态值是输入激活函数的值。
初始化方法为,
W ∼ U [ − 6 n i + n i + 1 , 6 n i + n i + 1 ] W \sim U[-\frac{\sqrt6}{\sqrt{n_{i} + n_{i + 1}}},\frac{\sqrt6}{\sqrt{n_{i} + n_{i + 1}}} ] W∼U[−ni+ni+16,ni+ni+16]Xavier初始化方法主要适用于tanh和sigmoid等S型曲线激活函数。
论文地址:Understanding the difficulty of training deep feedforward neural networks
He初始化(Kaiming初始化)
条件:正向传播时,状态值的方差保持不变;反向传播时,关于激活值的梯度的方差保持不变。
初始化方法为(适用于ReLU),
W ∼ N [ 0 , 2 n ^ i ] W \sim N[0,\sqrt{{\frac{2}{\hat{n}_{i}}}} ] W∼N[0,n^i2]在python中,实现方式是在随机初始化的基础上,乘以np.sqrt(u / layers_dims[l - 1])。layers_dims[l - 1]即上一层神经元的个数,u是一个可调的参数。经实践,对于tanh,u的取值为1;对于relu,u的取值为2。
He初始化方法主要适用于ReLU和Leaky ReLU等激活函数。
论文地址:Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
实验环境: python中numpy、matplotlib和sklearn库
import numpy as np
import matplotlib.pyplot as plt
import sklearn # 用于数据挖掘、数据分析和机器学习
import sklearn.datasets
训练样本: 300个带颜色点的二维坐标
测试样本: 100个带颜色点的二维坐标
训练样本和测试样本均由sklearn.datasets.make_circles函数生成。
train_X, train_Y = sklearn.datasets.make_circles(n_samples=300, noise=.05)
test_X, test_Y = sklearn.datasets.make_circles(n_samples=100, noise=.05)
关于本实验完整代码详见:
https://github.com/PPPerry/AI_projects/tree/main/4.weights_initialize
构建的神经网络模型如下:
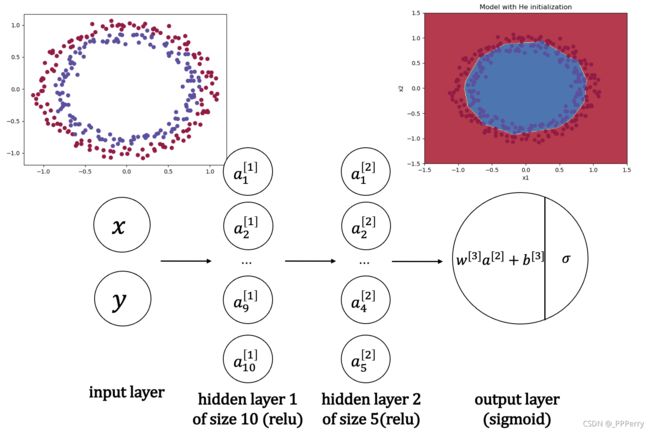
我们的目标就是通过训练这个神经网络来通过坐标值判断在坐标系中某一点可能的颜色,例如坐标(-4, 2)的点最可能是什么颜色,(1, -2)最可能是什么颜色。将红色和蓝色的点的区域区分出来。
基于该神经网络模型,代码实现如下:
其中,搭建网络的部分代码与人工智能系列实验(二)——用于区分不同颜色区域的浅层神经网络类似,这里不再赘述。主要是加载数据和实现不同初始化方法的部分。
首先,加载训练和测试数据。
def load_dataset():
train_X, train_Y = sklearn.datasets.make_circles(n_samples=300, noise=.05)
test_X, test_Y = sklearn.datasets.make_circles(n_samples=100, noise=.05)
plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral)
plt.show()
train_X = train_X.T
train_Y = train_Y.reshape((1, train_Y.shape[0]))
test_X = test_X.T
test_Y = test_Y.reshape((1, test_Y.shape[0]))
return train_X, train_Y, test_X, test_Y
绘制数据集如下:
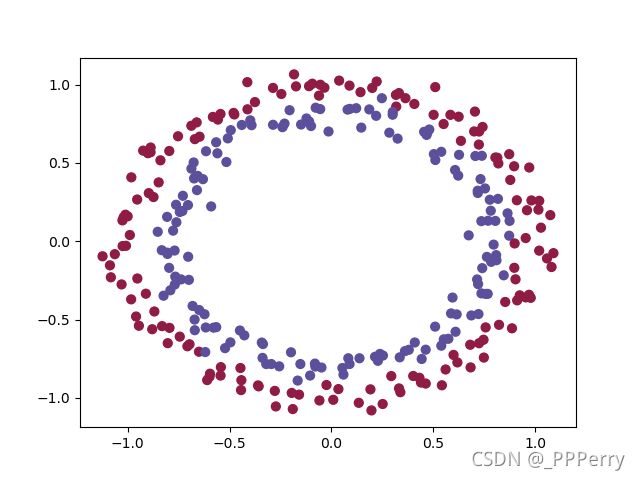
其次,构造神经网络中的初始化函数并依次观察预测结果。
1. 全0初始化
# 第一种方法——全0初始化
def initialize_parameters_zeros(layers_dims):
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
2. 随机初始化
# 第二种方法——随机初始化
def initialize_parameters_random(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
(这里我们故意增大了随机的参数值,方便更明显地比较与其他初始化方法的效果)
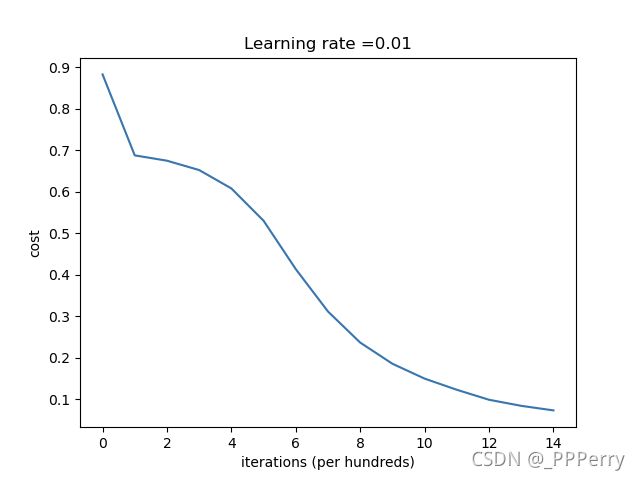
最终效果如下:
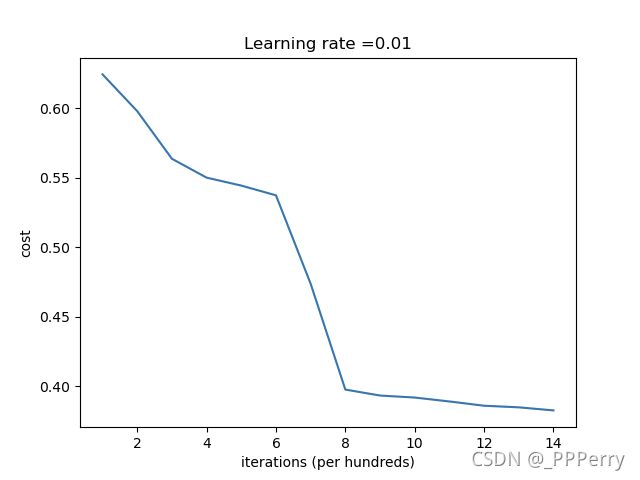
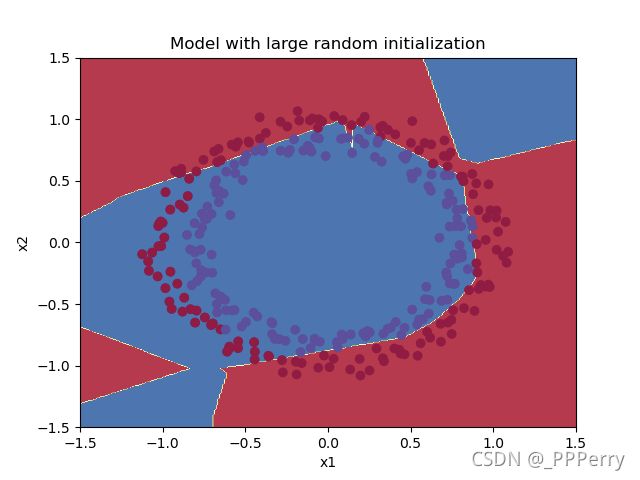
随机初始化的预测效果不是很好,参数初始化得不对会导致训练效率很差,需要训练很长时间才能靠近理想值。
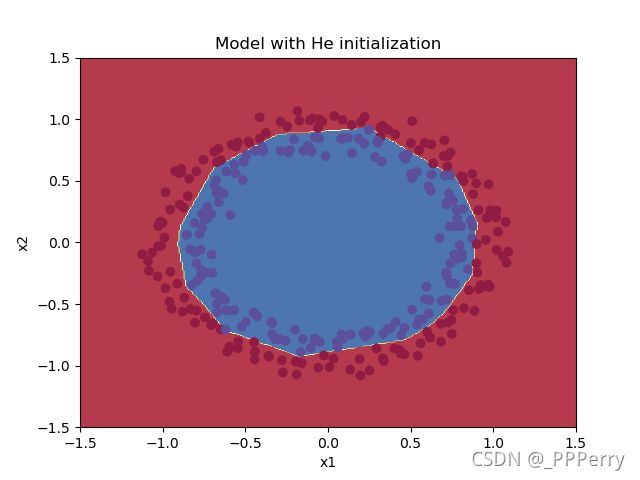
3. He初始化
# 第三种方法——He初始化
def initialize_parameters_he(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1
for l in range(1, L + 1):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
结束语:
在本实验中,我们可以明显看到,神经网络的模型均一致时,只是改变了对参数的初始化方法,预测效果就发生了质的变化。参数初始化方法的选择,对神经网络的预测准确率以及收敛速度等起着至关重要的作用。
往期人工智能系列实验:
人工智能系列实验(一)——用于识别猫的二分类单层神经网络
人工智能系列实验(二)——用于区分不同颜色区域的浅层神经网络
人工智能系列实验(三)——用于识别猫的二分类深度神经网络