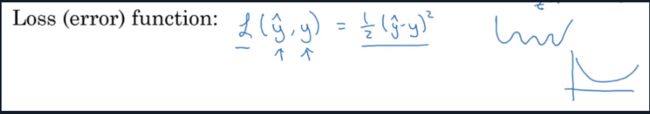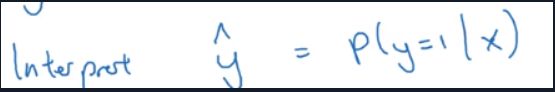Andrew Ng 神经网络与深度学习 week2

神经网络与深度学习

Logistic回归

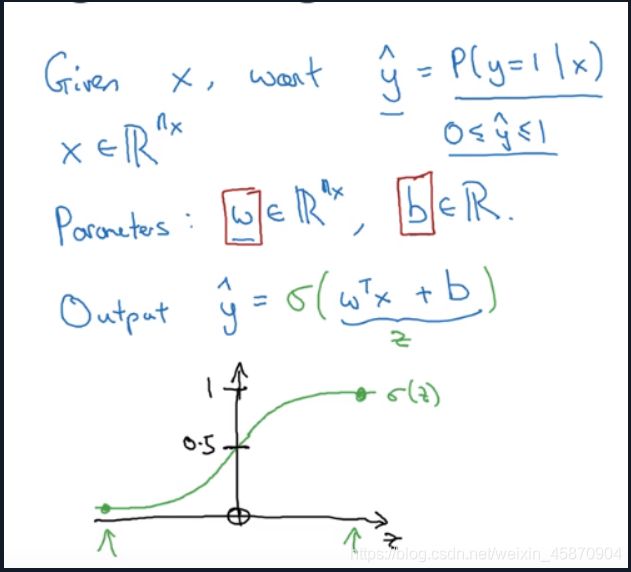
在Logistic回归中，我们需要得到的是y=1的概率 $$\hat{y}=p(y=1|x)$$，所以我们需要对线性回归拟合出的结果加一个激活函数(active function)-sigma function,来使得$$\hat{y}$$ 的取值范围位于[0,1]之间.

sigma

Logistic回归

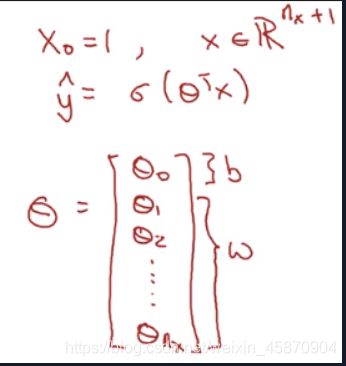
另一种表示法

Logistic回归的损失函数(cost function)

notation：

用i来关联每一个样本的数据

为什么convex function 被译作凸函数？

凹凸函数本质是描述函数斜率增减的。
语义上凸为正，代表斜率在增加（单调不减）。凹为负，代表斜率在减少。

Loss function（用于单个训练样本 ($$x^i,y^i$$))

用平方误差函数会是一个比较普遍的操作，但对于Logistic回归，用平方误差函数会造成损失函数不是凸函数的问题，所以对其使用梯度下降算法难以得到全局最优解，所以我们采用一种新的更够得到凸函数的loss function.

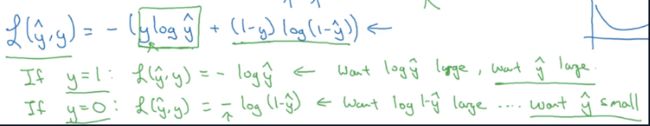
为什么Loss function是这样？

log函数是严格单调递增的函数，所以加上它并无影响

-是因为对于损失函数我们想要最小化它，而目前的函数我们需要最大化它

所以就得到了我们的loss function：

$$-[y^{(i)}log{\hat{y}}^{(i)}+(1-y^{(i)}log(1-{\hat{y}}^{(i)})]$$

cost function(衡量的在整个训练集上的表现)

cost function:
$$J(w,b)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log{\hat{y}}^{(i)}+(1-y^{(i)}log(1-{\hat{y}}^{(i)})]$$
训练就是为了得到能够使得其最小化的参数W和b

为什么cost function是这样？

训练样本都是IID（独立同分布的）

什么是独立同分布？

独立同分布independent and identically distributed (i.i.d.)

在概率统计理论中，如果变量序列或者其他随机变量有相同的概率分布，并且互相独立，那么这些随机变量是独立同分布。

在西瓜书中解释是：输入空间中的所有样本服从一个隐含未知的分布，训练数据所有样本都是独立地从这个分布上采样而得。

每一个特征都是一个$$\chi$$随机变量

在不少问题中要求样本数据采样自同一个分布，是因为希望用训练数据集得到的模型可以合理的用于测试数据集，使用独立同分布假设能够解释得通

使用独立同分布我目前的理解较为浅显的含义就是每个特征的采样都是独立同分布的

p(labels in traning set)=$$\prod p(y^{(i)}|x^{(i)})$$

我们使用最大似然估计的角度，得到一组参数使得给定样本的观测值概率最大

所以两边同取对数

梯度下降(gradient descent)

这里的图像我们假设的w和b都是实数 实际上 w可以是更高维的.

我们的cost function画出来是一个凸函数，所以我们达到了我们的目的

notation:

process:

这里偏导数没有用$$\alpha$$的原因是防止混淆 实际上在代码的编写中对于$$\frac{dj(w,b)}{dw}$$我们一般用dw进行代替

对于$$\frac{dj(w,b)}{db}$$我们一般用db进行代替

神经网络的基础表示-计算图(computation graph)

神经网络的建立基础就是正向传播和反向传播(bp)不断迭代的过程

在代码编写过程中 我们常常用 dvar来表示 最终变量(J或L)对于过程中某个变量的导数

例如 ：$$\frac{dFinaloutputvar}{dvar}=dvar$$

反向传播计算过程中，常用的是链式法则(chain rule): $$\frac{dj}{da}=\frac{dj}{dv}\frac{dv}{da}$$

Logistic regression中的梯度下降

Logistic regression中单个样本的导数计算图计算

logistic regression中m个样本的导数计算图计算

理论基础

一次梯度下降的过程

notation：

$$x_i$$代表的是第i个特征是一个随机变量 $$x^i$$代表的是某个特征的第i个样本

缺点： 这里我们需要双层for循环，导致时间复杂度大幅度增加从而变得很低效

第一层for循环需要遍历整个训练集（m次）

第二层for循环需要遍历所有的特征（n次）

所以我们需要用到向量化(Vectorization)

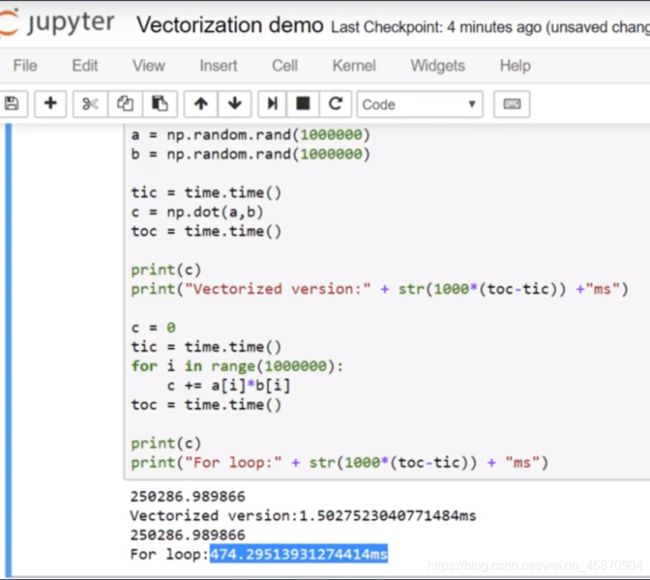
向量化

为什么向量化能够更快？

经过对比，我们可以看到 向量化的矩阵元素相乘速度要远远快于遍历相乘

之所以向量化能够更快的深层原因是编写向量化代码后 numpy能够充分地利用Gpu或者cpu提供的并行化计算功能

经验法则：只要有其他可能 就不要使用显式for循环

向量化的更多例子

经验法则：每次调用for循环的时候都想一下是否能够使用numpy的内置函数去替代它

向量化的Logistic regression

注意这里 W的维度是(nx,1)

注意每一个样本只有一个b 但可能有多个w和x 因为有多个特征向量

注意这里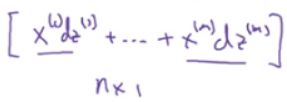
这个向量确实应该是n*1维度的，因为有n个特征 每一个样本已经相加成一个元素了 学过线性代数的应该明白 X的维度永远是(nx,m)

和以前的两个显式for循环的计算过程的对比

我们已经能够做到在一次梯度下降的过程中不用到任何for循环，当然做多次梯度下降的迭代for循环还是逃不掉

python中的广播

经验法则：多多使用reshape命令来得到你想要的矩阵的形状是不错的选择 其时间复杂度仅为O(1)

关于广播的法则：在前面的数据分析文章里面我有进行详细说明

这里我进行部分摘录：

1. 如果两个数组的维度数不相同，那么小维度数组的形状将会在最左边补1.
2. 如果两个数组的形状在任何一个维度上都不匹配，那么数组的形状会沿着维度为1的维度扩展以匹配另外一个数组的形状.
3. 如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于1，那么会引发异常

编写python代码时的小技巧

编写代码的时候要避免出现rank为1的向量，而需要显示地去定义其是列向量还是行向量

为了保证不会出错 后面可以加入assert 或者 reshape命令来保证我们的代码的安全性

*np.dot()是矩阵乘法 和np.multiply是元素乘法 numpy.outer(a, b)用来求外积

1、dot

①一维，计算内积，得到一个值

②多维，满足矩阵相乘

2、outer

①对于多维向量，全部展开变为一维向量

②第一个参数表示倍数，使得第二个向量每次变为几倍。

③第一个参数确定结果的行，第二个参数确定结果的列

编程作业tips：

1. np.exp(x) works for any np.array x and applies the exponential function to every coordinate

2. the sigmoid function and its gradient

3. image2vector is commonly used in deep learning

4. np.reshape is widely used. In the future, you’ll see that keeping your matrix/vector dimensions straight will go toward eliminating a lot of bugs.

5. numpy has efficient built-in functions

6. broadcasting is extremely useful

7. Vectorization is very important in deep learning. It provides computational efficiency and clarity.

8. You have reviewed the L1 and L2 loss.

9. You are familiar with many numpy functions such as np.sum, np.dot, np.multiply, np.maximum, etc…

正则化

L2范数

正则化中一般都采用L2范数，最多的度量距离欧氏距离就是一种L2范数

$$||x|{|}_2=\sqrt{\sum _{i=1}^n{x_i}^2}$$

还有平方差和等.L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力

python中用numpy计算范数

x_norm = np.linalg.norm(x,ord=2,axis=1,keepdims=True) #keepdims主要用于保持矩阵的二维特性

axis=1表示对列进行聚合计算每一行的范数 然后再用x/x_norm即可

来个栗子:

# GRADED FUNCTION: normalizeRows

def normalizeRows(x):
    """
    Implement a function that normalizes each row of the matrix x (to have unit length).
    
    Argument:
    x -- A numpy matrix of shape (n, m)
    
    Returns:
    x -- The normalized (by row) numpy matrix. You are allowed to modify x.
    """
    
    ### START CODE HERE ### (≈ 2 lines of code)
    # Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, axis = ..., keepdims = True)
    x_norm = np.linalg.norm(x,ord=2,axis=1,keepdims=True)
    
    # Divide x by its norm.
    x = x/x_norm
    ### END CODE HERE ###

    return x
    
Input:   x = np.array([
    [0, 3, 4],
    [1, 6, 4]])
print("normalizeRows(x) = " + str(normalizeRows(x))) 
Output:
    normalizeRows(x) = [[ 0.          0.6         0.8       ]
 [ 0.13736056  0.82416338  0.54944226]]

编程作业第二周：

每一张图片的数值化

each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).

每一张图片的像素值矩阵类型一般为(64,64,3)

3代表红黄蓝 64 64代表宽和高 所以后面我们flatten以后

一张图片就是(12288,1)的矩阵

把矩阵flatten的一种方法

A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b∗c∗d, a) is to use:

X_flatten = X.reshape(X.shape[0], -1).T      # X.T is the transpose of X

-1就是不知道有多少列，让计算机帮我算算有多少列

对于视觉图片我们需要将像素值标准化

To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.

One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).

Let’s standardize our dataset.

train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.

每一个像素值都是一个有三个属于[0,255]像素值的数字(红黄蓝)组成的向量

这里我们将其标准化 直接除以255(对每一行除以255)，从而使得所有的数字都位于[0,1]之间

向量化的参数计算代码

# GRADED FUNCTION: propagate

def propagate(w, b, X, Y):
    """
    Implement the cost function and its gradient for the propagation explained above

    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of size (num_px * num_px * 3, number of examples)
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)

    Return:
    cost -- negative log-likelihood cost for logistic regression
    dw -- gradient of the loss with respect to w, thus same shape as w
    db -- gradient of the loss with respect to b, thus same shape as b
    
    Tips:
    - Write your code step by step for the propagation. np.log(), np.dot()
    """
    
    m = X.shape[1]
    
    # FORWARD PROPAGATION (FROM X TO COST)
    ### START CODE HERE ### (≈ 2 lines of code)
    A = sigmoid(np.dot(w.T,X)+b)                                   # compute activation
    cost = (-1/m)*np.sum((Y*np.log(A))+(1-Y)*np.log(1-A))                              # compute cost
    ### END CODE HERE ###
    
    # BACKWARD PROPAGATION (TO FIND GRAD)
    ### START CODE HERE ### (≈ 2 lines of code)
    dw = (1/m)*(np.dot(X,(A-Y).T))
    db = (1/m)*np.sum(A-Y)
    ### END CODE HERE ###

    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost) #利用squeeze()函数将表示向量的数组转换为秩为1的数组
    assert(cost.shape == ())
    
    grads = {"dw": dw,
             "db": db}
    
    return grads, cost

值得注意的是 cost function这里我们使用的是元素乘法而不是矩阵乘法

A的维度是(12288.209) Y的维度是(1.209) 因为有209张图片 所以当然这里不应该利用矩阵乘法

而应该利用python广播进行元素相乘

编程作业中学到的知识

1. 调整学习率对于能够训练出一个好的模型是十分重要的

   [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qV6DWNUS-1612238136033)(C:\Users\QXY\AppData\Roaming\Typora\typora-user-images\image-20210130175956895.png)]

2. 对数据集进行预处理是十分重要的，例如居中和标准化

3. 函数式编程对于构建一个模型是十分重要的

4. cost算出来很低不一定是一件好事，也可能只是说明发生了过拟合而已

附录几个重要的函数源码：

def sigmoid(z):
    """
    参数：
        z  - 任何大小的标量或numpy数组。
    
    返回：
        s  -  sigmoid（z）
    """
    s = 1 / (1 + np.exp(-z))
    return s

def initialize_with_zeros(dim):
    """
        此函数为w创建一个维度为（dim，1）的0向量，并将b初始化为0。
        
        参数：
            dim  - 我们想要的w矢量的大小（或者这种情况下的参数数量）
        
        返回：
            w  - 维度为（dim，1）的初始化向量。
            b  - 初始化的标量（对应于偏差）
    """
    w = np.zeros(shape = (dim,1))
    b = 0
    #使用断言来确保我要的数据是正确的
    assert(w.shape == (dim, 1)) #w的维度是(dim,1)
    assert(isinstance(b, float) or isinstance(b, int)) #b的类型是float或者是int
    
    return (w , b)

def propagate(w, b, X, Y):
	"""
    实现前向和后向传播的成本函数及其梯度。
    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 矩阵类型为（num_px * num_px * 3，训练数量）
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据数量)

    返回：
        cost- 逻辑回归的负对数似然成本
        dw  - 相对于w的损失梯度，因此与w相同的形状
        db  - 相对于b的损失梯度，因此与b的形状相同
    """
	m = X.shape[1]
    
    #正向传播
    A = sigmoid(np.dot(w.T,X) + b) #计算激活值，请参考公式2。
    cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) #计算成本，请参考公式3和4。
    
    #反向传播
    dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
    db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。
	
	#使用断言确保我的数据是正确的
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    #创建一个字典，把dw和db保存起来。
    grads = {
                "dw": dw,
                "db": db
             }
    return (grads , cost)

def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
    """
    此函数通过运行梯度下降算法来优化w和b
    
    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数组。
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据的数量)
        num_iterations  - 优化循环的迭代次数
        learning_rate  - 梯度下降更新规则的学习率
        print_cost  - 每100步打印一次损失值
    
    返回：
        params  - 包含权重w和偏差b的字典
        grads  - 包含权重和偏差相对于成本函数的梯度的字典
        成本 - 优化期间计算的所有成本列表，将用于绘制学习曲线。
    
    提示：
    我们需要写下两个步骤并遍历它们：
        1）计算当前参数的成本和梯度，使用propagate（）。
        2）使用w和b的梯度下降法则更新参数。
    """
    
    costs = []
    
    for i in range(num_iterations):
        
        grads, cost = propagate(w, b, X, Y)
        
        dw = grads["dw"]
        db = grads["db"]
        
        w = w - learning_rate * dw
        b = b - learning_rate * db
        
        #记录成本
        if i % 100 == 0:
            costs.append(cost)
        #打印成本数据
        if (print_cost) and (i % 100 == 0):
            print("迭代的次数: %i ， 误差值： %f" % (i,cost))
        
    params  = {
                "w" : w,
                "b" : b }
    grads = {
            "dw": dw,
            "db": db } 
    return (params , grads , costs)

def predict(w , b , X ):
    """
    使用学习逻辑回归参数logistic （w，b）预测标签是0还是1，
    
    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数据
    
    返回：
        Y_prediction  - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组（向量）
    
    """
    
    m  = X.shape[1] #图片的数量
    Y_prediction = np.zeros((1,m)) 
    w = w.reshape(X.shape[0],1)
    
    #计预测猫在图片中出现的概率
    A = sigmoid(np.dot(w.T , X) + b)
    for i in range(A.shape[1]):
        #将概率a [0，i]转换为实际预测p [0，i]
        Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
    #使用断言
    assert(Y_prediction.shape == (1,m))
    
    return Y_prediction

def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
    """
    通过调用之前实现的函数来构建逻辑回归模型
    
    参数：
        X_train  - numpy的数组,维度为（num_px * num_px * 3，m_train）的训练集
        Y_train  - numpy的数组,维度为（1，m_train）（矢量）的训练标签集
        X_test   - numpy的数组,维度为（num_px * num_px * 3，m_test）的测试集
        Y_test   - numpy的数组,维度为（1，m_test）的（向量）的测试标签集
        num_iterations  - 表示用于优化参数的迭代次数的超参数
        learning_rate  - 表示optimize（）更新规则中使用的学习速率的超参数
        print_cost  - 设置为true以每100次迭代打印成本
    
    返回：
        d  - 包含有关模型信息的字典。
    """
    w , b = initialize_with_zeros(X_train.shape[0])
    
    parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
    
    #从字典“参数”中检索参数w和b
    w , b = parameters["w"] , parameters["b"]
    
    #预测测试/训练集的例子
    Y_prediction_test = predict(w , b, X_test)
    Y_prediction_train = predict(w , b, X_train)
    
    #打印训练后的准确性
    print("训练集准确性："  , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
    print("测试集准确性："  , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
    
    d = {
            "costs" : costs,
            "Y_prediction_test" : Y_prediction_test,
            "Y_prediciton_train" : Y_prediction_train,
            "w" : w,
            "b" : b,
            "learning_rate" : learning_rate,
            "num_iterations" : num_iterations }
    return d