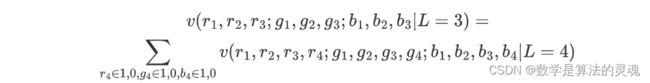MATLAB 图像处理大作业

1、基础知识

利用 MATLAB 提供的 Image file/IO 函数完成以下处理：

（a）以测试图像中心为圆心，图像长宽中较小值一半为半径画一个红颜色的圆；

（b）将测试图像涂成国际象棋状的‘黑白格’样子；

用一种看图软件浏览上述两个图，看是否达到目标。

第一题通过 rectangle 函数在图像上画圆，设置‘Curvature’为 1，即对应为圆；

load('hall.mat');
temp1 = hall_color;

imshow(temp1);
hold on;
[h,w,d] = size(temp1);              
r = min(h,w)/2;                 %取半径
rectangle('Position',[w/2-r,h/2-r,2*r,2*r],'Curvature',1,'LineWidth',1,'EdgeColor','r');
%画圆
saveas(gca,'temp1.png');

效果如图：

将图片涂成黑白棋盘形状，可以通过将图片分块，根据不同块的坐标决定是否进行涂黑操作。代码与效果如下：

block = 10;                 %单个格子的长度
for i = 0:floor(h/block)
    for j = 0:floor(w/block)
        if(mod(i+j,2)==1)
            i_end = (i+1)*block;
            j_end = (j+1)*block;
            if(h<(i+1)*block)
                i_end = h;
            end
            if(w<(j+1)*block)
                j_end = w;
            end 
            temp2(block*i+1:i_end,block*j+1:j_end,1) = 0;          
            temp2(block*i+1:i_end,block*j+1:j_end,2) = 0;
            temp2(block*i+1:i_end,block*j+1:j_end,3) = 0;
            %对三个通道进行涂黑
        end
    end
end
imwrite(temp2,'黑白.png','PNG');%写入文件

2、图像压缩编码

---

1）图像的预处理是将每个灰度值减去 128，这个步骤是否可以在变换域中进行？请选择一块进行验证

可以在变换域执行。由于对每个像素点减 128，相当于减去一个直流分量，也就相当于零频点强度减 128*x（x 未定）。

从数学上验证，设 A 为 N*N 的待处理矩阵，D 为 DCT 算子，O 为全 1 矩阵，则减去 128 后得到的 C 为：

从而，即将 C~0,0~ 减去 128*N 即可；

代码验证如下：

load('hall.mat');%载入数据A=double(hall_gray(1:8,1:8));%转换类型，便于处理D_1=0:7;D_1=D_1';D_2=1:2:15;D=D_1*D_2;D=cos(D*pi/2/8);D(1,:)=D(1,:)/sqrt(2);DD=D/2;%生成8*8的DCT算子C=D*(A-128*ones(8,8))*D';%所有元素减去128后的DCT变换C2=D*A*D';C2(1,1)=C2(1,1)-128*8;%直接在变换域做处理p=my_equal(C2,C);%判断是否相等all(p)

结果显示 C 与 C2 相等，得证。

2）

请编程实现二维 dct，并与 MATLAB 自带的库函数 dct2 比较是否一致

由指导书中知识，只需构造 DCT 算子 D，随后对矩阵 A 进行运算，变换域矩阵 C=DAD^T^。若 A 不为方阵，由构造原理，先对 A 的每列进行 DCT 变换，在对变换后的矩阵的每行进行 DCT 变换，即

$$ C=D_{M*M}A_{M*N}D_{N*N}^T; $$

故而在代码中，通过自定义的 DCT_operator 函数可以方便地生成 N 维 DCT 算子，随后进行如上计算即可。

代码如下：

function B = my_dct2(A)
%对A做dct变换[M,N]=size(A);D1=DCT_operator(M);D2=DCT_operator(N);B=D1*A*D2';

DCT_operator 函数定义如下：

function D = DCT_operator(N)
%返回DCT算子D[r,c]=size(N);if(r~=1&&c~=1)error('Input must be a single number');endD=zeros(N);D1=0:N-1;D2=1:2:2*N-1;D=D1'*D2;D=cos(D*pi/2/N);D(1,:)=D(1,:)/sqrt(2);D=D*sqrt(2/N);

随意构造一个随机矩阵 A，计算 my_dct2 与 dct2 的结果，可以发现结果一致；

3）如果将 DCT 系数矩阵中右侧四列的系数全部置零，逆变换后的图像会发生什么变化？验证你的结论。如果左侧四列变为 0 呢？

选取 hall_gray 的 120 列、120 行作为测试图像，做 DCT 变换后得到系数矩阵 C。将 C 的右 4 列、左 4 列分别置为 0，随后做逆变换，显示图像结果如下：

可以看出，将 DCT 系数矩阵右 4 列变为 0 后，图像没有明显变换，但是将左 4 列变为 0，图像明显变黑。从中可以看出人眼对于低频分量的变化较为敏感。且将左 4 列变为 0，相当于去掉了直流分量及低频分量，整体图像变暗。当然，N 越大，则右边 4 列变为 0 的影响越小。

代码如下：

N=120;A=double(hall_gray(1:N,1:N))-128;%预处理B=my_dct2(A);C=dct2(A);C2=C;C2(:,N-4:N)=0;%右边4列为0D=DCT_operator(N);%N阶DCT算子A2=D'*C2*D;%DCT逆变换A2=uint8(A2);%数据类型变换subplot(1,3,1);%绘图imshow(A2);title('右4列变0');subplot(1,3,2);C3=C;C3(:,1:4)=0;%左4列变0A3=D'*C3*D;%DCT逆变换imshow(uint8(A3));title('左四列变0');subplot(1,3,3);imshow(uint8(A));title('原图');

4）若对 DCT 系数分别做转置、选择 90 度和旋转 180 度操作，逆变换后恢复的图像有何变化？请选择一块图验证你的结论。

对 DCT 系数做转置，相当于对原图片进行转置。证明如下：

$$ A'=D^TC^TD=D^T*(D*A^T*D^T)*D=A^T $$

对 DCT 矩阵旋转 90 度，180 度，猜测逆变换后图像也有旋转，但不好从数学上说明；

效果图、代码如下：

A=double(hall_gray(1:N,1:N))-128;D=DCT_operator(N);C=dct2(A);%转置C1=C';A1=D'*C1*D+128;%旋转90度C2=rot90(C);A2=D'*C2*D+128;%旋转180度C3=rot90(C,2);A3=D'*C3*D+128;

可以看出，旋转后逆变换的图像，除了旋转，相较于原图变化很大，但还是可以大致看出大礼堂的形状。

5）如果认为差分编码是一个系统，请绘出这个系统的频率响应，说明它是一个滤波器。DC 系数先进行差分编码再进行熵编码，说明 DC 系数的频率分量更多。

差分系统表达式可写为：

$$ y(n)= \begin{cases} x(n-1)-x(n),&\text{n！=1；}\

x(1),&\text{n=1;}\

\end{cases} $$

故而

$$ H(z)=\frac{1}{z^{-1}-1} $$

代码如下：

b = [-1 1];
a = 1;
freqz(b,a,2001);

图像如下：

由此可见，差分编码系统为高通滤波器。DC 系数先进行差分编码，说明高频率分量更多。

6）DC 预测误差的取值和 Category 值有何关系？如何利用预测误差算出其 Category？

观察 Category 的计算表，可以得知，每个 Category 的值对应于区间：

$$ [-2^n-1,-2^{n-1}], [2^{n-1},2^n-1]\

n为category,n>0; $$

由此 Category 的计算公式为：

$$ Category = \begin{cases} floor(log_2|x|)+1, &x!=0;\

0,&x=0; \end{cases} \x为预测误差 $$

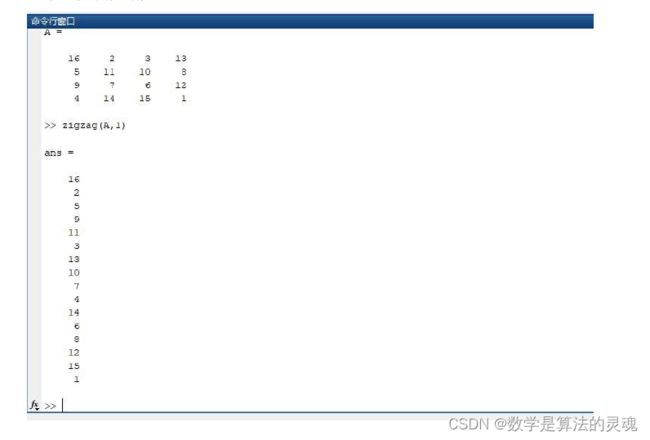
7)你知道哪些 zigzag 扫描的方法？请利用 MATLAB 的强大功能设计一种最佳方法。

要实现 zig_zag，有以下两种思路：

1.打表法，通过写出 zigzag 扫描得到的列向量对应的 8*8 矩阵转为的列向量中的下标，即可方便地进行 zigzag 扫描。然而该方法只适用于固定大小矩阵。

2.扫描法：通过程序直接模拟 zigzag 扫描，从而可以进行任意大小矩阵的 zigzag 扫描。具体方法为，定义一个方向指示变量 dir，每次循环都会为列向量 y 添加元素。定义 i，j 代表矩阵元素下标，每次判断该位置元素是否为边界终止点，从而确定下一次扫描的点的下标所在。

综上，定义了 zigzag()函数来进行 zigzag 扫描，扫描方法作为参数传入，详见 zigzag.m 文件；

%模拟zigzag扫描
    dir = 1;        %方向变量，1代表向上扫描，0代表向下扫描
    i = 1;
    j = 1;
    num = 1;
    normal_move = 0;
    for index = 1:r*c
        i,j
        y(index) = A(i,j);
        if(i==1 | j==1 | i==r | j==c) %到达边界
            if( dir & j==c ) %于右边界到达终点
                i = i+1;
                dir = ~dir; %改变方向
            elseif( dir & i==1 )%于上边界到达终点
                j = j+1;
                dir = ~dir;
            elseif( ~dir & i==r )%于下边界达到终点
                j = j+1;
                dir = ~dir;
            elseif( ~dir & j==1 )%于左边界达到终点
                i = i+1;
                dir = ~dir;
                
            else    %说明是起点
                if(dir==1)  %正常移动
                    i=i-1; j=j+1;
                else 
                    i=i+1; j=j-1;
                end
            end
            
        else
            if(dir==1)  %正常移动
                i=i-1; j=j+1;
            else 
                i=i+1; j=j-1;
            end
        end
    end

打表方法如下：

if(r~=8 | c~= 8)
    error('A must be an 8*8 matrix,otherwise you should use method 1');
end
    
index = [1,9,2,3,10,17,25,18,11,4,5,12,19,26,33,41,...
        34,27,20,13,6,7,14,21,28,35,42,49,57,50,43,36,...      	29,22,15,8,16,23,30,37,44,51,58,59,52,45,38,31,24,32,39,46,53,...
        60,61,54,47,40,48,55,62,63,56,64];
x = A(:);
for i = 1:64
    y(i) = x(index(i));
end

通过验证可知程序正确性：

8）对测试图像分块、DCT 和量化，将量化后的系数写成矩阵形式，其中每一列为一个块的 DCT 系数经过 zigzag 扫描后形成的列矢量，第一行为各个块的 DCT 系数。

将测试图像分块，DCT，量化后结果写入矩阵中，每列为一块 DCT 系数结果 zigzag 扫描后的列矢量。代码思路大致分为如下步骤：

1. 对图像进行补全，使得行、列数正好为 8 的倍数；

2. 利用 for 循环进行分块，每次选取一个块作为变量 block，用于后续处理；

3. 对 block 做减去 128 的预处理；

4. 对 block 进行 DCT 变换； . 对 DCT 系数进行 zigzag 扫描后，结果写入对应的结果矩阵中。

具体代码如下（详见 ex2_8.m)，结果存于 ex2_8_result 中：

A=double(hall_gray);%先对测试图像进行补全[rc]=size(A);if(mod(r,8)~=0)A(r+1:(floor(r/8)+1)*8,:)=0;endif(mod(c,8)~=0)A(:,c+1:(floor(c/8)+1)*8)=0;end%随后开始分块[rc]=size(A);result=zeros(64,r*c/64);fori=1:r/8forj=1:c/8block=A(8*(i-1)+1:8*i,8*(j-1)+1:8*j);%分块完成block=block-128;%预处理D=dct2(block);%DCT变换D=round(D./QTAB);%量化result(:,(i-1)*c/8+j)=zigzag(D,2);%zigzag扫描endend

9）请事先本章介绍的 JPEG 编码（不包括写 JFIF 文件），输出为 DC 系数的码流、AC 系数码流、图像高度和宽度，将四个变量写入 jpegcodes.mat 中。

为了实现 JPEG 编码，首先定义两个函数 DC_coeff（）与 AC_coeff（），分别用于求出每个块的 DC 码与 AC 码；

函数代码如下：

function DC_code = DC_coeff(DC_vector)
%输入直流分量的向量DC_vector%输出DC为其对应的二进制码流D=zeros(length(DC_vector),1);D(2:length(DC_vector))=-diff(DC_vector);D(1)=DC_vector(1);%差分编码DC_code='';load('JpegCoeff.mat');fori=1:length(D)DC_code=strcat(DC_code,DC_translate(D(i),DCTAB));endend

其中调用到自定义的子函数 DC_translate（），用于将预测误差通过已知的 DCTAB 表进行翻译。其代码如下：

function y = DC_translate(c,DCTAB)
%y为DC系数翻译的二进制字符串%c为预测误差%DCTAB即为对应的码表y='';cor=0;%cor为Categoryif(c~=0)cor=floor(log2(abs(c)))+1;ends_length=DCTAB(cor+1,1);fori=1:s_lengthy=strcat(y,DCTAB(cor+1,1+i)+'0');end%查表，Huffman编码s=dec2bin(abs(c));if(c<0)fori=1:length(s)if(s(i)=='1')s(i)='0';elseif(s(i)=='0')s(i)='1';endendend%预测误差的二进制码       y=strcat(y,s);end

随后用课件中的例子进行简单验证，大致没有问题。

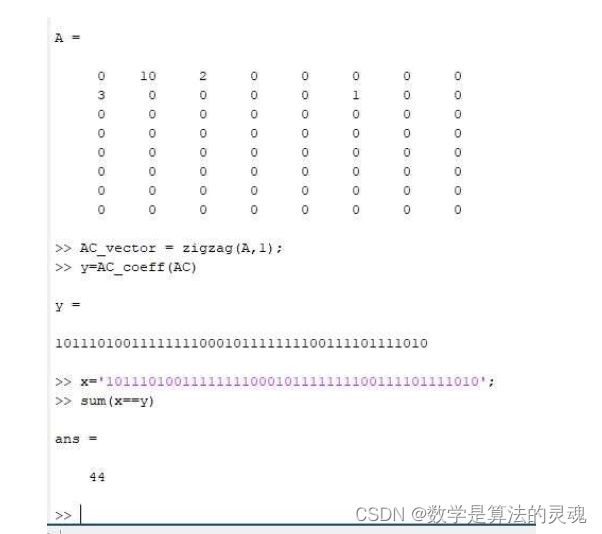
AC_coeff()函数同理，代码以及验证（同课件上的例子）如下:

function y = AC_coeff(AC_vector)
%输入AC_vector为经过量化的待处理的AC系数%输出y为对应的二进制码流load('JpegCoeff.mat');run=0;y='';ZRL='11111111001';%16连0EOB='1010';%块结束符fori=1:length(AC_vector)if(AC_vector(i)==0)run=run+1;elseif(run<16)y=strcat(y,AC_translate(run,AC_vector(i),ACTAB));%添加该非0系数的二进制码run=0;elsewhile(run>=16)y=strcat(y,ZRL);run=run-16;endy=strcat(y,AC_translate(run,AC_vector(i),ACTAB));endendendy=strcat(y,EOB);%在结尾增加EOBendfunction y = AC_translate(run,c,ACTAB)
%该函数为子函数%run为游程数%c为非零AC系数%ACTAB为Huffman对照表%返回值y对应AC系数二进制码size=0;if(c~=0)size=floor(log2(abs(c)))+1;end%确定该系数的sizeamplitude=dec2bin(abs(c));if(c<0)fori=1:length(amplitude)if(c(i)=='0')c(i)='1';elseif(c(i)=='1')c(i)='0';endendend%确定amplitudehuffman='';row=run*10+size;l=ACTAB(row,3);fori=1:lhuffman=strcat(huffman,ACTAB(row,3+i)+'0');end%确定run/size的huffman编码y=strcat(huffman,amplitude)%返回值end

随后需要对整幅图像进行 jpeg 编码，由于在之前的题目中已经得到了 DCT 系数的结果矩阵 result，该矩阵的第一行即为 DC 系数，该矩阵每列第二道末尾为 AC 系数。故只需进行循环即可得到 DC 与 AC 的二进制码。于是在结构上采用上一题的程序，增加以下语句完成整幅图像的编码：

DC=result(1,:);%第一行即为DC系数H=r;%高W=c;%图像宽度DC_code=DC_coeff(DC);%DC码AC_code='';%AC码fori=1:r*c/64%逐块翻译AC码AC_code=strcat(AC_code,AC_coeff(result(2:end,i)));end%将结果写入结构体中jpegcodes=struct('DC_code',{DC_code},'AC_code',AC_code,'H',H,'W',W);save'jpegcodes.mat'jpegcodes

结果通过一个结构体 jpegcodes 存入 jpegcodes.mat 中。

10）计算压缩比（输入文件长度/输出码流长度），注意转换为相同进制。

在灰度图中，一个像素占一字节，由测试图像的长宽可计算出图像文件大小为 20160B。

DC 码流与 AC 码流均为二进制码，其长度即为其 bit 数。

代码如下：

[r,c]=size(hall_gray);pic_size=r*c;%计算原始图像字节数code_length=length(jpegcodes.DC_code)+length(jpegcodes.AC_code);%计算码流长度ratio=pic_size*8/code_length%字节数乘8后除于码流长度即为压缩比

结果如下：

若考虑上写入文件中的图像长度、宽度数据，每个数据假设为 int8 型，则相当于码流长度再加上 16bits，计算出的压缩比为 6.4107。由此可见，JPEG 编码方式可以节省许多内存空间。

11）请实现本章介绍的 JPEG 解码，输入是你生成的 jpegcodes.mat 文件，分别用客观和主观方式评价。

对生成的压缩信息做解压，主要分为以下几个步骤：

5. 对 DC、AC 码进行熵解码，虽然 MATLAB 自带 Huffman 编码，但是由于 DC、AC 码流中除了 Huffman 码外还有二进制数，故不能直接将码进行处理；若想采用逐个输入解码的话，MATLAB 会报错，综上考虑，决定自己根据已有的编码表构造出 Huffman 二叉树，从而进行解码的工作。每个 Huffman 码解码后再将二进制数还原，最终将（8）问中的 result 矩阵还原出来。构建 Huffman 树的工作写于函数文件 build_huffmantree.m 中，关键代码如下：

fori=1:r%共有r个编码row=encode_table(i,:);value_number=row(1);%值的个数code_number=row(2+value_number);%编码长度index=1;code=row(3+value_number:3+value_number+code_number-1);%获取codefork=1:length(code)%对tree进行构造if(code(k)==0)if(tree(index).left~=0)%若存在left节点index=tree(index).left;%读取下一个节点indexelsetree(length(tree)+1)=struct('left',0,'right',0,'value',-1);%创建新节点tree(index).left=length(tree);%对left进行赋值index=length(tree);%disp(strcat('create a new node, index:',num2str(index)));endelseif(code(k)==1)if(tree(index).right~=0)%若存在right节点index=tree(index).right;%读取下一个节点indexelsetree(length(tree)+1)=struct('left',0,'right',0,'value',-1);%创建新节点tree(index).right=length(tree);%创建新节点index=length(tree);endelseerror('code should not contain numbers otherwise 1,0');endendtree(index).value=row(2:value_number+1);%定义节点的value即为解码结果end

由以上代码即可构造出一课 Huffman 编码树，每个叶子节点的 value 值对应于该 Huffman 码的数值。故而每次从根节点开始遍历，直达节点到达叶子节点，即可找到这段码对应的数值。

随后对整段 DC 码流进行解码，每次解码完后，根据 Category 解出后面几位二进制码代表的预测误差，随后继续循环 Huffman 解码。如此便可解出 DC 码流。

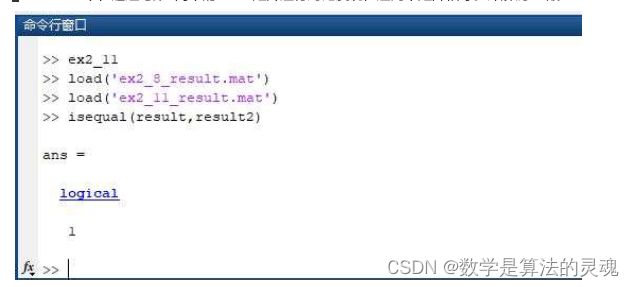
index=1;tree_index=1;%用于指示树中节点位置find_end=0;%用于指示是否完成一段的解码while(index

对于 AC 码同理，不再赘述。但是在 AC 码的还原中出现了许多 bug，由此发现前面进行 AC 码编码函数就存在着些许 bug，经过修改后整个部分终于得以成功运转。综上得到原有的 result 矩阵。将该 result 矩阵存在 ex2_11_result.mat 下，通过与第 8 问中的 result 矩阵进行对比发现，这两个矩阵相等。即解码正确。

6. 对该 result 矩阵的每列进行反 zigzag 还原，还原成 8*8 矩阵。

为了简单起见，采用打表法，由于之前已经存在下标对照表，只需将赋值的顺序发过来即可，关键代码如下：

index=[1,9,2,3,10,17,25,18,11,4,5,12,19,26,33,41,...34,27,20,13,6,7,14,21,28,35,42,49,57,50,43,36,...29,22,15,8,16,23,30,37,44,51,58,59,52,45,38,31,24,32,39,46,53,...60,61,54,47,40,48,55,62,63,56,64];%zigzag的对应索引y=zeros(64,1);fori=1:64y(index(i))=s(i);			%反过来对应endy=reshape(y,8,8);%变为矩阵

7. 随后对每块矩阵进行反量化，随后进行 DCT 逆变换；

代码如下：

column=result2(:,i);%取一列block=anti_zigzag(column);%还原图像块block=block.*QTAB;%反量化pic_block=idct2(block);%逆DCT2

8. 将各块进行拼接；

r_index=ceil(i/c);c_index=mod(i,c);if(c_index==0)c_index=c;end%确定图像块所处的位置pic(8*r_index-7:8*r_index,8*c_index-7:8*c_index)=pic_block;%拼接

综上，将各步骤合成为单个函数 picture_recover()，从而可以方便地调用函数进行解码。解码结果以及 PSNR 计算结果如下：

PSNR = 34.8975，可以看出在 30——40dB 间，查询维基百科可知，一般的图像压缩 PSNR 值就在 30——40dB 间，可以看出压缩效果较好。

从主观上来看，这两幅图看不出明显差别，但是解压后的图像显得更加顺畅平缓（图中大礼堂门口的柱子处）由此可见，Jpeg 的确是一种优秀的图像压缩方式。

12）将量化步长减小为原来的一半，重做编解码。同标准量化步长的情况比较压缩比与图像质量。

此步只需将 JpegCoeff.mat 中的 QTAB 矩阵改为原来的一半后计算压缩比与 PSNR 即可。故在每步使用到 QTAB 时将 QTAB 减半即可。

更改后结果如下：

QTAB	压缩比	PSNR	主观感受
原版	6.4188	34.8975	看不出明显变化
一半	4.4081	37.3897	看不出明显变化

由此可见，将 QTAB 减半后，压缩比减小到 4.4，PSNR 则有所增大。但是由于本来的图像质量就较好，故而外面倾向于选择压缩比更大的量化矩阵。

13）看电视时偶尔可以看到美丽的雪花图像（见 snow.mat），请对其进行编码，和测试图像压缩比与图像质量进行比较，并解释比较结果。

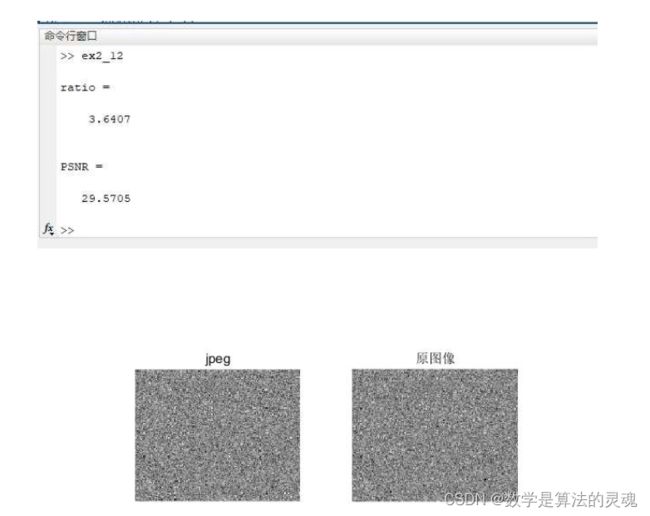
将图像压缩的过程组合成函数 JPEG_encoder，输出结构体 jpegcodes，压缩比、PSNR 以及解压图像结果如下：

可以看出，与之前的测试图像结果进行对比，压缩比减小了许多，同时，PSNR 也下降了许多，说明对于这种雪花图像的压缩效果并不好。原因在于雪花图像是随机图像，与我们日常看到的图像存在不同，图像上并不连续，而 jpeg 是根据人眼对连续亮度的东西较为敏感而设计的，故而压缩效果很差。

3、信息隐藏

---

1）实现本章介绍的空域隐藏方法和提取方法。验证其抗 JPEG 编码能力

首先，需要得到待隐藏信息。在这里为了简单起见，将字符串设置为待隐藏信息，并且转化为其对应的 ascii 码（二进制），从而得到一个二进制的数组，数组结尾带 8 个 0，代表到达字符结尾。待隐藏信息存于'msg.mat'中。

%generate messagemessage='Tsinghua University';bin_msg=[];fori=1:length(message)msg=binstr2array(dec2bin(abs(message(i))))';%转为二进制数组msg=[zeros(1,8-length(msg)),msg];%每个字符对应8位bin_msg(end+1:end+8)=msg;endbin_msg(end+1:end+8)=zeros(1,8);savemsg.matbin_msg

要实现空域隐藏方法，只需将图像每个像素中最低位换为信息即可。由于每个像素最低位代表其是否为奇数，故只需对待接收信息的像素先减去最低位，再加上信息大小即可。相关代码如下：

[r,c]=size(hall_gray);hall=double(hall_gray(:));%将信息载体先转为列向量l=length(bin_msg);if(r*c

由上图可见，修改最低位对于图像基本没有影响。完全无法看出图片中隐藏着信息。若要对该图进行信息提取，只需将该图每个像素的最低位提取出来，随后根据之前的约定，当某一位为全 0 时，即找到了结尾位，由此可以得到每个字符的信息，从而还原出字符串。

%信息提取code=mod(hall2(:),2);%取最低位recover_msg=[];%字符数组fori=1:floor(length(code)/8)zifu=code(8*i-7:8*i);%取连续8位zifu=zifu.*(2.^(7:-1:0)');%乘对应的幂if(sum(zifu)~=0)recover_msg(end+1)=sum(zifu);elsebreak;%说明到达结尾endendrecover_msg=char(recover_msg)%转为字符串

结果如图，可见还原成功。

随后对隐藏信息的图像进行 JPEG 编码以及解码，对解码后的图像进行提取信息操作，结果如下：

由于 JPEG 编码为有损编码，故提取信息为乱码。可见空域信息隐藏非常不抗 JPEG 编码。

2）依次实现本章介绍的三种变换域信息隐藏方法与提取方法，分析嵌密方法的隐蔽性以及嵌密后图像的质量变化和压缩比变化

a.同空域方法，用信息为逐一替换掉每个量化后的 DCT 系数的最低位，在进行熵编码

要将每一位 DCT 系数都进行替换，但是要隐藏的信息可能没有那么长，在此不妨做如下规定：对于要隐藏的文本信息，最后面全部补为 0，从而使得信息长度与图像 DCT 系数（像素个数）一致，从而对每个 DCT 系数都作出修改。

但是还有一个问题需要考虑，DCT 系数不同于像素，其值存在负值。考虑到负数的二进制 2 补码表示中，最低位为 1 时为奇数。故而可以采用判定其是否为奇数来推断最低位。

综上所述，将以上功能封装成函数 msg_hide()与 msg_take()，详细定义参见该两个函数文件。其中该两个函数均有参数 method 代表采用的是第几种 DCT 域信息隐藏方法。同时为了方便地得到图片的全部块的 DCT 系数矩阵，自定义函数 DCT_result()；

关键代码如下：

result=result(:);%result变为列向量result=result-mod(result,2);%使每个DCT系数的最后一位都为0if(length(msg_array)

随后对得到的 result 矩阵进行熵编码，代码与之前一致，在此略去。

图像质量与压缩比评价如下：

可以看出加密后压缩比变小，且相比于正常图片 JPEG 编码后的结果，加密后图像质量下降较多。

b.同方法 1，用信息位逐一替换掉每个量化后的 DCT 系数的最低位，在进行熵解码。注意不是每个 DCT 系数都嵌入了信息。

此种方法减少了对 DCT 系数的修改。要实现只对部分 DCT 系数做修改，且能提取信息，需要做一些规定。在此处我进行的规定是当读取到停止位（即 8 个 0）时，说明信息已经提取完毕。当然也可以采取在开头写入信息的长度之类的方式。做此修改后即可实现方法 2。

关键代码如下：

result=result(:);%result变为列向量l=length(msg_array);if(l>length(result))l=length(result);endresult(1:l)=result(1:l)-mod(result(1:l),2);%使每个DCT系数的最后一位都为0result(1:l)=msg_array(1:l)+result(1:l);%修改部分result=reshape(result,r,c);

图像质量与压缩比评价如下：

可以看出，图像质量较于第一种方法有了明显的上升。但是由于此时要隐藏的信息大小较小，如果信息量很大的话，那就需要修改更多的 DCT 系数甚至修改全部的 DCT 系数，此时与第一种方法无异。故此种算法会使得图像质量随着信息量增大而变差。在信息量较小时的确不失为一种好方法。

c.先将待隐藏信息用 1,-1 的序列表示，再逐一将信息为追加在每个快 zigzag 顺序的最后一个非零 DCT 系数之后，若原本该图像块的最后一个系数就不为零，那就用信息为替换该系数。

用此方法只能实现一个块隐藏 1bit 信息，相对之前的方法来说可隐藏信息量大幅减少。实现上较为简单，关键代码如下：

l=size(result,2);%图像的块数if(l>length(msg_array))l=length(msg_array);endfori=1:l
	column=result(:,i);index=length(column);%最后一个非0系数的下标find=0;
  	while(~find)if(column(index)~=0)
    	find=1;
  	elseindex=index-1;endend%由此找到最后一个非零系数indexif(index==length(column))
	column(index)=msg_array(i);elsecolumn(index+1)=msg_array(i);end%将信息写入result(:,i)=column;

图像质量与压缩比信息如下：

可以看出此种方法对图像质量的影响较小，但是与第二种方法相比较并没有明显优势，甚至稍微劣势于第二种方法。且能隐藏的信息量

取决于图像块的数量，与前两种方法相比，差距还是较大的。

但是我们不妨将得到的图片展示出来，从主观上判断：

从图像上来看，前两种方法获得的图像的左上角都有很明显的噪声块，且第一种方法导致的图像失真较明显。而第三种方法从肉眼上看并没有明显的噪声块存在。由此可以判定，方法 3 的隐蔽性远远高于前两种方法。原因在于方法 3 只是选取高频的 DCT 系数进行改变，而人眼对于高频分量并不敏感，所以并不能看出明显的差别。而前两种方法对于低频 DCT 系数都存在修改，故而较为容易发现其隐藏了信息。综上列出如下评价表：

method	压缩比	图像质量	隐蔽性
1	变小	变差	差
2	稍微变小（信息量较少时）	稍微变差（信息量较小时）	差
3	稍微变小	稍微变差	良好

3）（选做）请设计实现新的隐藏算法并分析其优缺点。

没想好，暂时空着。

4、人脸识别

---

1）所给资料 Faces 目录下包含从网图中截取的 28 张人脸，试以此作为样本训练人脸标准 v

a)、样本人脸大小不一，是否需要首先将图像调整为相同大小？

不需要。因为训练方法只是对图像中的所有像素点的颜色，计算其中各个颜色出现的频率，得到特征 u(R)，与图像大小没有关系。

b)、假设 L 分别取 3、4、5，所得的三个 v 之间有何关系？

当 L 选取 3/4/5 时，意味着对于每个 uint8 只选取其前 3/4/5 位作为特征。故而 L 越大，v 中每个元素包含的信息量越大。而 L 越小，v 中每个点对应的颜色数目就越多。例如：L 为 3 的 v 中每个元素（即该颜色的概率密度）对应于 L 为 4 的 v 中，RGB 前 3 位相同的颜色的概率密度之和。对于 L 为 5 同理。数学表达如下：

2)设计一种从任意大小的图片中检测任意多张人脸的算法并编程实现（输出图像在判定为人脸的位置加上红色的方框）。随意选取一张多人照片（比如支部活动或者足球比赛），对程序进行调试。尝试 L 分别取不同的值，评价检测结果有何区别。

设计算法各个步骤如下：

1. 根据训练集训练出特征标准 v；

2. 输入图像并对图像做分块处理（类似于 JPEG 编码）;

3. 对于每块图像块 R，计算其特征 u(R)；

4. 计算 u(R)与 v 的度量系数系数，与阈值比较，判定该块是否为人脸；

5. 将相邻的人脸块统一并进行标识（用方框围住）；

以下进行该算法的程序实现与结果测试：

（1）训练特征标准

观察 Faces 中的训练样本，每张图片基本都是人脸，仅有少数的其它干扰，故我们可以认为训练集中的图片仅由人脸构成。故而我们定义函数 feature_extract()来对单张图片进行特征提取，编写 train.m 脚本实现训练，并将得到的标准特征 v 存入文件 face_standard.mat 中。

feature_extract()的关键代码如下：

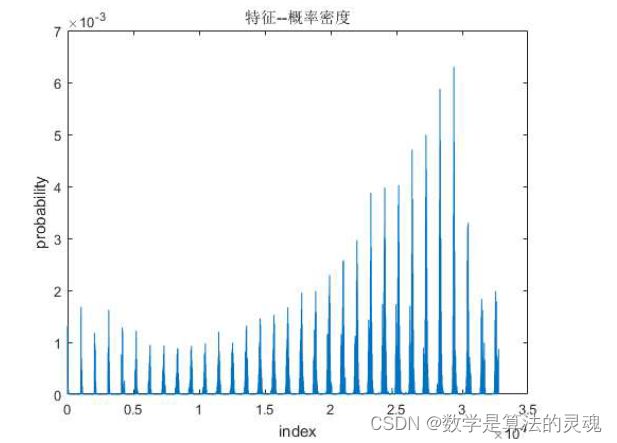
pic=double(reshape(pic,size(pic,1)*size(pic,2),1,3));v=zeros(2^(3*L),1);basic=2^(8-L);%初始化fori=1:size(pic,1)a=[pic(i,1,1),pic(i,1,2),pic(i,1,3)];%取出像素index=sum(floor(a/basic).*(2.^(2*L:-L:0)))+1;%计算该颜色对应的下标v(index)=v(index)+1;%次数+1endv=v/size(pic,1);%循环统计每个颜色出现的次数并求出频率

train.m 关键代码如下：

fori=1:numv=v+feature_extract('Faces/',strcat(num2str(i),'.bmp'),L);endv=v/num;

得到的结果 v 如图（L=5）:

(2) 输入图像并对其分块处理

不妨尝试取 block_l 长的正方形大小的图像块进行处理（16<=block_l<=50,依图像不同而有变化），取图像块顺序为逐行取（同 JPEG 编码），但有一点不同，此处若每行最后一块大小不足 block_l*block_l 大小，并不进行补全，而是直接取剩下的即可。此块代码较简单，且类似于 JPEG 编码中的分块，不在此赘述。详见 face_detect()函数。

(3) 计算图像块特征

与训练特征标准中的对单张图片求特征的方法一致。不再赘述。

(4) 计算度量系数，从而进行检测

u=feature_extract(block,L);		%提取图像块特征cor=sqrt(u).*sqrt(v);				%计算系数ifcor>=threshold					%大于阈值identify(i,j)=1;				%对应图像块判定为人脸end

但是在此处阈值需要设定的较好，方可有较好的识别效果。为此写了一个脚本来对不同阈值的效果进行对比（即效果图全部显示），随后用手工的方法挑选最佳阈值。效果图大致如下：

(5) 将相邻的方块统一并进行标识

此处只需将相邻的方块进行合并，忽略单独的小方块即可。合并代码可以见文 face_detect.m 修改后效果图如下（好看多了）：

(6) 测试

此处我们选择一张多人照片进行测试：

可以看出，虽然检测出人脸，但是方框的范围过大，总的来说 L=6 的情况似乎较好一些。此处问题的原因在于，合并各块结果并画方框时，我采用的是只要相邻就判定为同一张人脸，故而对于多人图来说，极有可能造成几张人脸最终被合成一个方框的惨剧。故而我们在测试多人图时将画方框的代码注释后再进行测试。

由上面结果可以看出，其实算法的确将人脸部分检测出（还包含一些皮肤部分），但是由于这些方块相邻，故而合并方框的代码并不能很好地执行。所以在接下来的演示中依旧采用不合并方框的代码。对于不同 L，只要阈值设置好，结果基本相近。但个人更喜欢 L=4/5 。

3.对上述图像分别进行如下处理后

（a）顺时针旋转 90 度

（b）保持高度不变，宽度拉伸为原来的 2 倍（imresize）

（c）适当改变颜色（imadjust）

再试试你的算法检测结果如何？并分析所得结果。

代码如下：

L=4;threshold=0.27;subplot(2,2,1);img=imread('test.jpg');[y,num,identify]=face_detect(img,L,thresholds(L-2));title('原图');subplot(2,2,2);img2=rot90(img);[y,num,identify]=face_detect(img2,L,thresholds(L-2));title('旋转90度');subplot(2,2,3);img3=imresize(img,[size(img,1)2*size(img,2)],'nearest');[y,num,identify]=face_detect(img3,L,thresholds(L-2));title('调整图像宽度');subplot(2,2,4);img4=imadjust(img,[.2.30;.6.71],[]);[y,num,identify]=face_detect(img4,L,thresholds(L-2));title('调整图像颜色');

结果如下：

可以看出，对图像旋转、更改大小后，对于检测没有什么影响。但是对于颜色做出修改后，无法检测出人脸。原因就在于算法是基于训练出的颜色的，若将颜色改变较多，则无法有效地进行识别。而颜色与旋转、改变大小等操作无关，故而结果基本一致。

（4）如果可以重新选择人脸样本训练标准，你觉得该如何选取？

个人认为可以增加人脸样本数量。并且可以针对不同人种设定不同的人脸训练集合（例如黄种人、白种人、黑人训练集分开），从而得到不同的人脸肤色标准，从而可以对一张图中不同肤色的人脸有较好的识别能力。

（5） 人脸识别部分感想：

感觉人脸识别部分通过肤色来进行人脸识别，虽然可以识别到人脸，但是皮肤等部分也会被包括进去，故而存在一些局限性。 同时，在检测后，对识别出的人脸进行方框标识的算法也较简单，比较适用于单人图或者多人但是人脸隔得较远的图。 总的来说，通过本章部分，对人脸识别有了个初步的认识。

5、文件列表

---

文件	说明
pic	报告中使用到的图片
Faces	人脸识别训练集
temp1.png	练习 1_2 结果图
黑白.png	练习 1_2 结果图
ex2_8_result.mat	存储 DCT 系数矩阵（每列为一个图像块经 zigzag 扫描后的一列）
jpegcodes.mat	存储经过 JPEG 编码信息的结构体（有 4 个变量域：DC_code,AC_code,H,W）
ex2_11_result.mat	经过解码后得到的 DCT 系数矩阵，用于与 2_8 中的矩阵进行对比来验证解码函数的正确性
msg.mat	用于给 ex3_1 提供待隐藏信息
face_standard.mat	储存 L=3 到 6 所训练出的人脸判别标准矢量
test.jpg/test2.jpg/test3.jpg	人脸识别用的测试图像
AC_coeff.m	对一列向量进行 AC 编码
AC_decoder.m	对 AC 码进行解码
anti_zigzag.m	对数组进行反 zigzag 还原（限 8*8 矩阵）
binstr2array.m	将 0,1 组成的字符数组转化为数组
build_huffmantree.m	由编码表建立 Huffman 树
DC_coeff.m	用于 DC 编码
DC_decoder.m	用于 DC 解码
DCT_operator.m	构建 DCT 算子
DCT_result.m	将图像转为 DCT 系数矩阵（量化后的）
face_detect.m	检测图像中的人脸并标注
feature_extract.m	从图像块中提取颜色特征
JPEG_decoder.m	对 JPEG 文件进行解码
JPEG_encoder.m	对图片进行 JPEG 编码
msg_generate.m	产生 msg.mat
msg_hide.m	将信息隐藏进图片
msg_take.m	提取信息
my_dct2.m	实现 DCT 变换
my_equal.m	在误差范围内判断是否相等
picture_recover.m	从 jpegcodes 恢复图像
result_recover.m	从 jpegcodes 恢复 DCT 系数矩阵
train.m	训练人脸识别标准
zigzag.m	对图像块进行 zigzag 扫描
exx_x.m	对应练习题 x_x
MATLAB 图像处理大作业.md	Markdown 版实验报告（推荐用 Typora 阅览）

完整代码：

https://mp.csdn.net/mp_download/manage/download/UpDetailed