分类器评价指标 ROC,AUC,precision,recall,F-score,多分类评价指标
目录
一、定义
二、ROC曲线
三、如何画ROC曲线
详解ROC/AUC计算过程(roc计算非常详细)
四、AUC
AUC值的计算
AUC的计算方法(两个公式并且都举了例子)
为什么使用ROC曲线
五:准确率,召回率,F值
六、K-S 曲线、Lift 曲线、PR 曲线
七、 多分类评价指标
kappa系数
一、定义
ROC (Receiver Operating Characteristic) 曲线和 AUC (Area Under the Curve) 值常被用来评价一个二值分类器 (binary classifier) 的优劣
多分类问题评价指标:precision,recall,F-score
在分类任务中,人们总是喜欢基于错误率来衡量分类器任务的成功程度。错误率指的是在所有测试样例中错分的样例比例。实际上,这样的度量错误掩盖了样例如何被分错的事实。在机器学习中,有一个普遍适用的称为混淆矩阵(confusion matrix)的工具,它可以帮助人们更好地了解分类中的错误。
比如有这样一个在房子周围可能发现的动物类型的预测,这个预测的三类问题的混淆矩阵如下表所示:
一个三类问题的混淆矩阵
利用混淆矩阵可以充分理解分类中的错误了。如果混淆矩阵中的非对角线元素均为0,就会得到一个近乎完美的分类器。
二、ROC曲线
ROC曲线:接收者操作特征曲线(receiver operating characteristic curve),是反映敏感性和特异性连续变量的综合指标,roc曲线上每个点反映着对同一信号刺激的感受性。
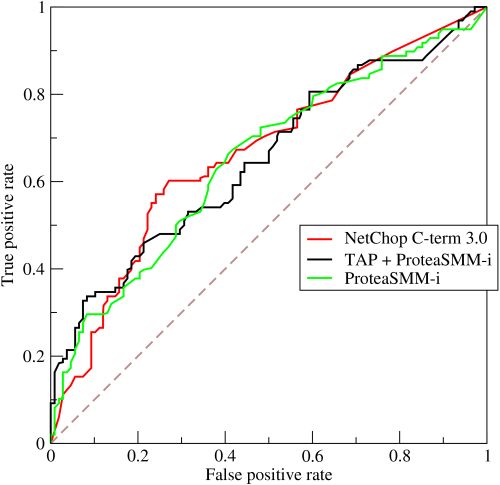
对于分类器,或者说分类算法,评价指标主要有precision,recall,F-score等,以及这里要讨论的ROC和AUC。下图是一个ROC曲线的示例:
- 横坐标:1-Specificity,伪正类率(False positive rate, FPR),预测为正但实际为负的样本占所有负例样本的比例;
- 纵坐标:Sensitivity,真正类率(True positive rate, TPR),预测为正且实际为正的样本占所有正例样本的比例。
在一个二分类模型中,假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
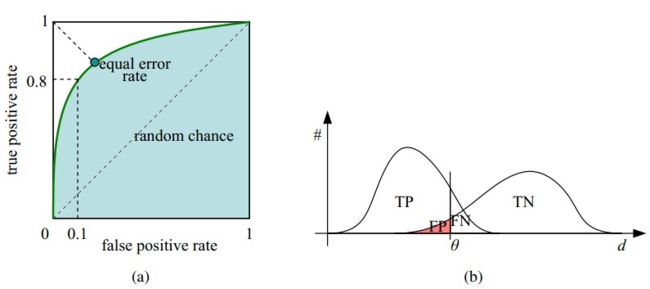
如下面这幅图,(a)图中实线为ROC曲线,线上每个点对应一个阈值。
(a) 理想情况下,TPR应该接近1,FPR应该接近0。ROC曲线上的每一个点对应于一个threshold,对于一个分类器,每个threshold下会有一个TPR和FPR。比如Threshold最大时,TP=FP=0,对应于原点;Threshold最小时,TN=FN=1,对应于右上角的点(1,1)。
(b) P和N得分不作为特征间距离d的一个函数,随着阈值theta增加,TP和FP都增加。
- 横轴FPR:1-TNR,1-Specificity,FPR越大,预测正类中实际负类越多。
- 纵轴TPR:Sensitivity(正类覆盖率),TPR越大,预测正类中实际正类越多。
- 理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好,Sensitivity、Specificity越大效果越好。
三、如何画ROC曲线
详解ROC/AUC计算过程(roc计算非常详细)
http://www.voidcn.com/article/p-yyudlykx-cb.html
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值,这又是如何得到的呢
我们忽略了分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。通过更深入地了解各个分类器的内部机理,我们总能想办法得到一种概率输出。通常来说,是将一个实数范围通过某个变换映射到(0,1)区间。
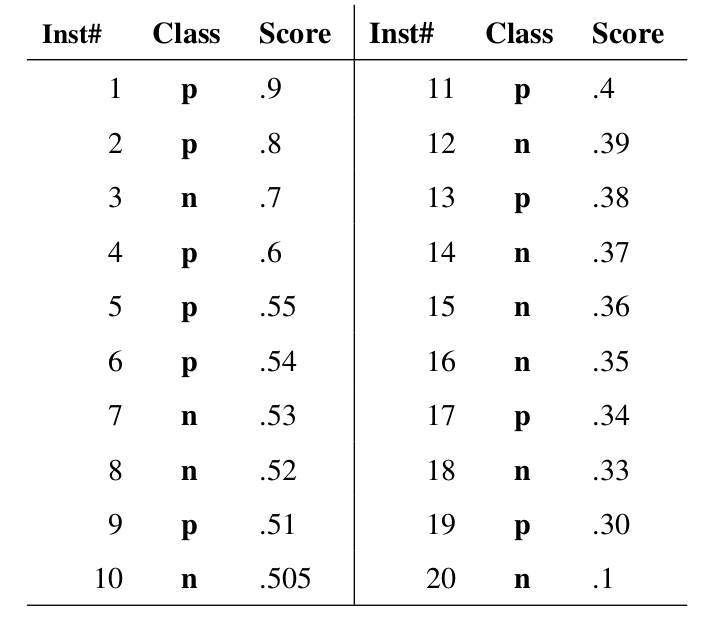
假如我们已经得到了所有样本的概率输出(属于正样本的概率),现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
其实,我们并不一定要得到每个测试样本是正样本的概率值,只要得到这个分类器对该测试样本的“评分值”即可(评分值并不一定在(0,1)区间)。评分越高,表示分类器越肯定地认为这个测试样本是正样本,而且同时使用各个评分值作为threshold。我认为将评分值转化为概率更易于理解一些。
四、AUC
AUC值的计算
AUC (Area Under Curve) 被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
AUC的计算有两种方式,梯形法和ROC AUCH法,都是以逼近法求近似值,具体见wikipedia。
AUC的计算方法(两个公式并且都举了例子)
https://blog.csdn.net/qq_22238533/article/details/78666436
这句话有些绕,我尝试解释一下:首先AUC值是一个概率值,当你随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然,AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
从AUC判断分类器(预测模型)优劣的标准:
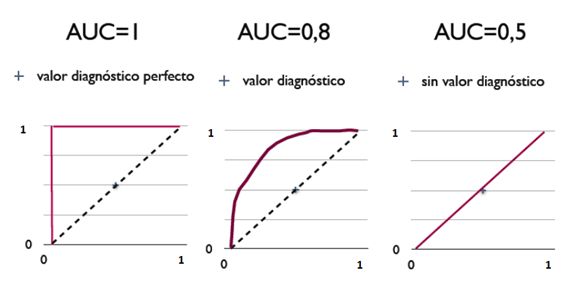
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
三种AUC值示例:
简单说:AUC值越大的分类器,正确率越高。
为什么使用ROC曲线
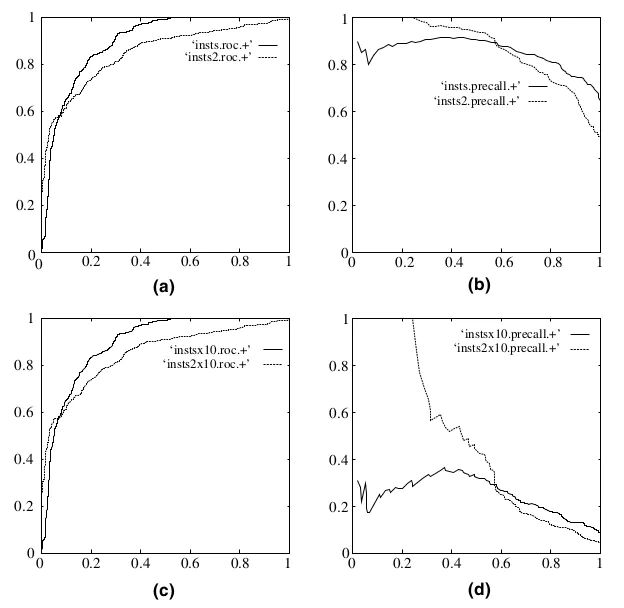
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比:
在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
五:准确率,召回率,F值
TP-将正类预测为正类
FN-将正类预测为负类
FP-将负类预测位正类
TN-将负类预测位负类
- 准确率(正确率)=所有预测正确的样本/总的样本 (TP+TN)/总
- 精确率= 将正类预测为正类 / 所有预测为正类 TP/(TP+FP)
- 召回率 = 将正类预测为正类 / 所有正真的正类 TP/(TP+FN)
精确率、精度(Precision)
精确率(precision)定义为:![]()
表示被分为正例的示例中实际为正例的比例。
召回率(recall)
召回率是覆盖面的度量,度量有多个正例被分为正例,recall=TP/(TP+FN)=TP/P=sensitive,可以看到召回率与灵敏度是一样的。
综合评价指标(F-Measure)
P和R指标有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score)。
F-Measure是Precision和Recall加权调和平均:![]()
当参数α=1时,就是最常见的F1,也即![]()
可知F1综合了P和R的结果,当F1较高时则能说明试验方法比较有效。(F 值即为正确率和召回率的调和平均值)
六、K-S 曲线、Lift 曲线、PR 曲线
ROC、K-S 曲线、Lift 曲线、PR 曲线
https://www.zhihu.com/search?type=content&q=Lift%E6%9B%B2%E7%BA%BF
七、 多分类评价指标
https://blog.csdn.net/wf592523813/article/details/95202448
kappa系数
kappa系数是用在统计学中评估一致性的一种方法,取值范围是[-1,1],实际应用中,一般是[0,1],与ROC曲线中一般不会出现下凸形曲线的原理类似。这个系数的值越高,则代表模型实现的分类准确度越高。![]()
- P0表示总体分类精度
- Pe表示SUM(第i类真实样本数*第i类预测出来的样本数)/样本总数平方

from sklearn.metrics import cohen_kappa_score
kappa = cohen_kappa_score(y_true,y_pred,label=None) #(label除非是你想计算其中的分类子集的kappa系数,否则不需要设置)
海明距离
海明距离也适用于多分类的问题,简单来说就是衡量预测标签与真实标签之间的距离,取值在0~1之间。距离为0说明预测结果与真实结果完全相同,距离为1就说明模型与我们想要的结果完全就是背道而驰。
from sklearn.metrics import hamming_loss
ham_distance = hamming_loss(y_true,y_pred)
杰卡德相似系数
它与海明距离的不同之处在于分母。当预测结果与实际情况完全相符时,系数为1;当预测结果与实际情况完全不符时,系数为0;当预测结果是实际情况的真子集或真超集时,距离介于0到1之间。我们可以通过对所有样本的预测情况求平均得到算法在测试集上的总体表现情况。
from sklearn.metrics import jaccard_similarity_score
jaccrd_score = jaccrd_similarity_score(y_true,y_pred,normalize = default)
#normalize默认为true,这是计算的是多个类别的相似系数的平均值,normalize = false时分别计算各个类别的相似系数
铰链损失
铰链损失(Hinge loss)一般用来使“边缘最大化”(maximal margin)。损失取值在0~1之间,当取值为0,表示多分类模型分类完全准确,取值为1表明完全不起作用。
from sklearn.metrics import hinge_loss
hinger = hinger_loss(y_true,y_pred)