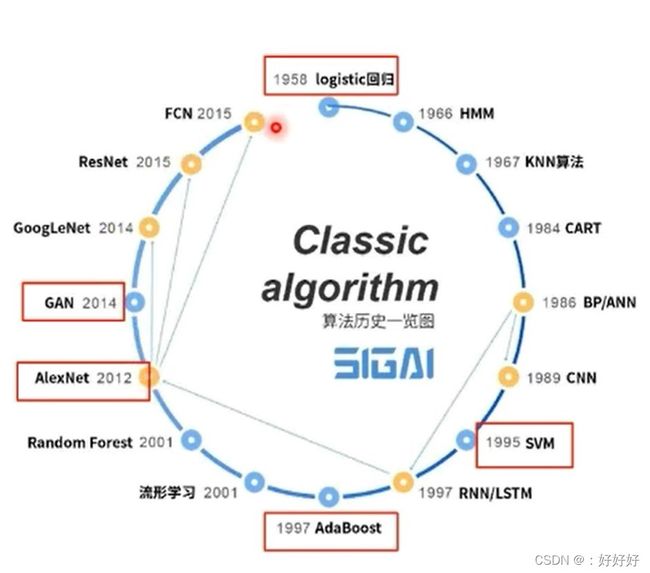
毕业设计Week1
图片源于网络,若有侵权,联系删除。
这次学习分为了2个部分。第一个部分是视频学习部分,第二个部分是代码学习部分。
Part1 视频学习
视频1 引论
1️⃣ 图灵测试
在黑盒外判断盒内是一个人还是一个机器。
Ex:验证码系统。
2️⃣ GAN
二战中盟军破解了德国的Enigma系统:通过模拟Enigma密码生成的过程来破解,这种思路体现在了今天的对抗式生成网络(GAN)中。
Keywords:深度学习模型,无监督学习,(至少)两个模块(生成模型(Generative Model)、判别模型(Discriminative Model))
原始 GAN 理论中,并不要求 G 和 D 都是神经网络,只需要是能拟合相应生成和判别的函数即可。但实用中一般均使用深度神经网络作为 G 和 D。
判别模型:给定一张图,判断这张图里的动物是猫还是狗
生成模型:给一系列猫的图片,生成一张新的猫咪(不在数据集里)
3️⃣ 人工智能的三个层面
5️⃣ 逻辑演绎 与 归纳总结

6️⃣ 机器学习
keywords:解出一个 近似解。
实际应用中,特征往往比分类器更重要。
- 模型、策略、方法。
模型(对要学习问题映射的假设)
根据已有的数据集,知道输入和输出结果之间的关系。根据这种已知的关系,训练得到一个最优的模型。
什么是有监督、无监督、强化学习?
参数指的是数据分布的参数。参数模型能预先对数据分布进行假设。
生成模型对输入和输出的联合分布建模
判别模型对输入条件下输出的条件分布建模
特征提取:从原始数据中提取一些有效的特征。
特征转换:对特征进行一定的加工,如升维降维。
特征抽取:PCA,LDA
特征选择:互信息,TF-IDF
- 传统机器学习 与 深度学习
A.Rule-based systems
Hand-designed program
B.Classic machine learning
Hand-designed feature
Mapping from features
C.Simple representation learning
Features
Mapping from features
D.Deep learning
Simple features
More complex features
Mapping from features
从上至下,人的作用在削弱,机器自主学习的能力在增强。
视频2 深度学习概述
1️⃣ 深度学习的“不能”
1.算法输出不稳定,容易被“攻击”
Ex:对抗样本,改变一个像素值。
2. 模型复杂度高,难以纠错和调试
3. 模型层级复合程度高,参数不透明
Ex:Inception(GoogLeNet),残差,门结构
Inception

残差(ResNet)
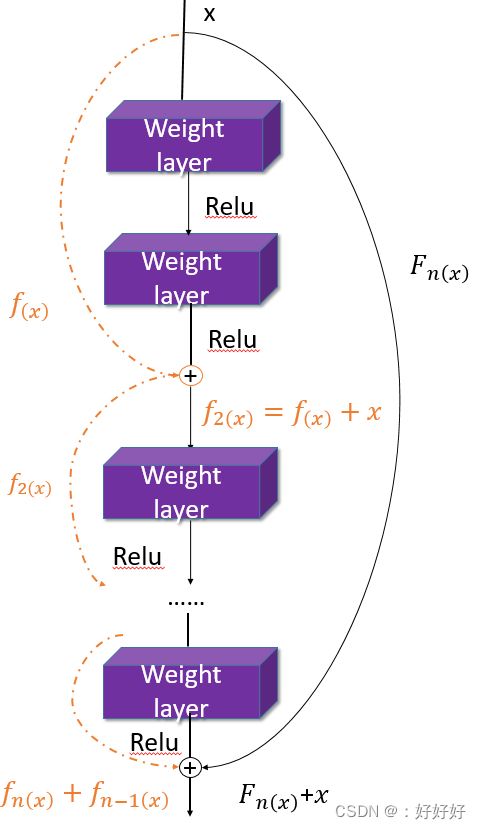
4.端到端训练方式对数据依赖性强,模型增量性差
T e s t l o s s − T r a i n i n g l o s s ≤ N m Test loss - Training loss ≤ \sqrt{\frac{N}{m}} Testloss−Trainingloss≤mN
m:训练样本
N:模型有效容量
5. 专注直观感知类问题,对开放性推理问题无能为力
6. 人类无法有效引入进行监督,机器偏见难以避免
2️⃣ 解释性 与 泛化性
 3️⃣ M-P神经元
3️⃣ M-P神经元
y = f( ∑ 1 n \sum_1^n ∑1nwixi - Θ \Theta Θ)
4️⃣ 激活函数
1.线性函数(Ex:恒等函数)
2.斜面函数
3.阈值函数(Ex:阶跃函数)
4.符号函数
5️⃣ Sigmoid函数
y(x) = 1 1 + e < s u p > − x < / s u p > \frac{1}{1+{e{-x}}} 1+e<sup>−x</sup>1
y(x)’ = y(x)(1 - y(x))
6️⃣ 单层感知机
我自己理解为,可以学习的MP神经元,参数w不是预先设置的。
6️⃣ 多层感知机
具有多个神经元层
有多个隐层的感知机
7️⃣ 万有逼近定理
如果一个隐层包含足够多的神经元,三层前馈神经网络(输入-隐层-输出)能以任意精度逼近任意预定的连续函数。
y = a(W * x + b)
完成输入->输出空间变换
W * x:升维/降维;放大/缩小;旋转
+b:平移
a(·):弯曲
更深、更宽,并不一定能增强效果。
8️⃣ 梯度消失
连续求导以后,每个导数的值都非常小,导致最终结果接近于0。
9️⃣ 误差反向传播
F(x) = fn(fn-1…f2(f(x) * Θ \Theta Θ1 + b) * Θ \Theta Θ2 +b)…)
比较实际与最终结果的差,差为正则降低权重;反之则增加权重。
可以通过Learning Rate来调整
所以BP算法很容易过拟合(在训练集上表现很好,但是在新数据集上不佳),可以采用提前停止的方法来改善,用训练集调整参数,用验证集调整误差。
Part2 代码学习
Pytorch中的基本操作
import torch
x = torch.tensor(666)
print(x)
# 一维
x = torch.tensor([1, 2, 3, 4, 5, 6])
# 二维
# 二行三列的矩阵
x = torch.ones(2, 3)
# 任意维度
x = torch.ones(2,3, 4)
# 创建一个空张量, x行y列
x = torch.empty(x, y)
# 创建一个随机初始化的张量
x = torch.rand(5, 3)
# 创建一个全0的张量,里面的数据类型为 long
x = torch.zeros(5,3,dtype=torch.long)
# 用已知的张量初始化一个新的张量
y = x.new_ones(5,3)
# 重新定义原来tensor的类型
z = torch.randn_like(x, dtype = torch.float)
# 输出
print(m\[0][2])
print(m[:, 1])
# 矩阵相乘
m @ v
# 矩阵转置(3种方法)
print(m.t())
print(m.transpose(0, 1))
print(m.permute(1, 0))
Spiral classifciation
import random
import torch
from torch import nn, optim
import math
from IPython import display
from plot_lib import plot_data, plot_model, set_default
# 因为colab是支持GPU的,torch 将在 GPU 上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('device: ', device)
# 初始化随机数种子。神经网络的参数都是随机初始化的,
# 不同的初始化参数往往会导致不同的结果,当得到比较好的结果时我们通常希望这个结果是可以复现的,
# 因此,在pytorch中,通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)
N = 1000 # 每类样本的数量
D = 2 # 每个样本的特征维度
C = 3 # 样本的类别
H = 100 # 神经网络里隐层单元的数量
torch.manual_seed(seed)的使用是为了方便复现
设置随机种子后,是每次运行文件的输出结果都一样
将所有最开始读取数据时的tensor变量copy一份到device所指定的GPU上去,之后的运算都在GPU上进行。
多GPU时
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model = Model()
if torch.cuda.device_count() > 1:
model = nn.DataParallel(model,device_ids=[0,1,2])
model.to(device)
转:多GPU情况下的代码
X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
index = 0
t = torch.linspace(0, 1, N) # 在[0,1]间均匀的取10000个数,赋给t
# 下面的代码不用理解太多,总之是根据公式计算出三类样本(可以构成螺旋形)
# torch.randn(N) 是得到 N 个均值为0,方差为 1 的一组随机数,注意要和 rand 区分开
inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
# 每个样本的(x,y)坐标都保存在 X 里
# Y 里存储的是样本的类别,分别为 [0, 1, 2]
for ix in range(N * c, N * (c + 1)):
X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
Y[ix] = c
index += 1
print("Shapes:")
print("X:", X.size())
print("Y:", Y.size())
torch.linspace(0, 1, N),将区间(0,1)均分为N份