Pytorch——线性回归和逻辑回归学习笔记
回归
线性回归
线性回归是利用数理统计中的回归分析来确定两种或两种以上变量间相互依赖的定量关系的一种统计方法。
一元线性回归
回归分析中只包含一个自变量和因变量,且二者的关系可用一 条直线近似表达,直线为全部数据点的一元线性回归分布
损失函数
是用来拟合直线和真实值之间的距离的,损失函数越小,说明训练数据与直线拟合的越好。
某预测值^y 与真实值y之间的距离就是该点的损失(loss ——如图红线标记)

计算所有数据点与拟合直线的距离之和的函数为损失函数
loss = ∑(f(xi) - yi)^2
一元线性回归的代码实现
线性回归属于监督学习,其实思路为先给定一个训练集,根据这个训练集学习出一个线性函数,然后检测这个函数训练的好不好,从而选择最好的函数,最后用这个最好的函数完成训练。
#导入包,导入Torch模块库和Matplotlib画图模块库
import torch as t
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from torch.autograd import Variable
#定义超参数——超参数:在开始学习前设置的参数,相应的,其他参数的值是通过训练得出的
input_size = 1
output_size = 1
num_epochs = 1000#迭代的次数,迭代一次相当于使用训练集中地全部样本训练一次
learning_rate = 0.001#学习率:每次参数更新的制度大小
#制造数据,即生成矩阵数据
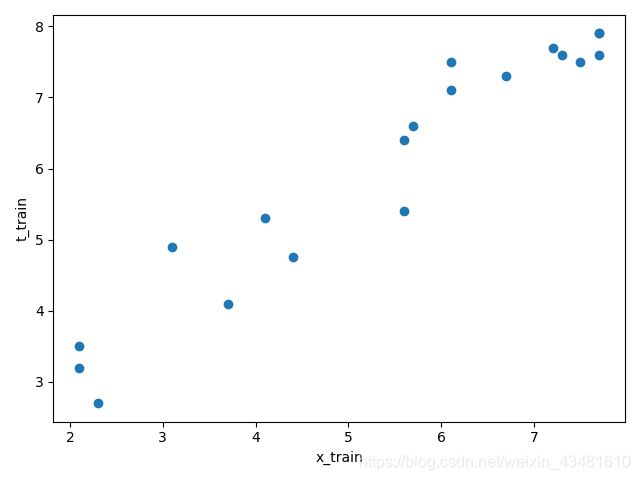
x_train = np.array([[2.3],[4.4],[3.7],[6.1],[7.3],[2.1],[5.6],[7.7],[7.7],[4.1],[6.7],[6.1],[7.5],[2.1],[7.2],[5.6],[5.7],[7.7],[3.1]],dtype = np.float32)
#xtrain生成矩阵数据
y_train = np.array([[2.7],[4.76],[4.1],[7.1],[7.6],[3.5],[5.4],[7.6],[7.9],[5.3],[7.3],[7.5],[7.5],[3.2],[7.7],[6.4],[6.6],[7.9],[4.9]],dtype = np.float32)
plt.figure()#画散点图
plt.scatter(x_train,y_train)
plt.xlabel('x_train')#x轴的名称
plt.ylabel('y_train')#y轴的名称
plt.show()
#第三步,建立回归模型
# nn.Linear表示的是y = wx + b
# input_size 表示的是自变量x的尺寸,是一维
# output_size 表示的是因变量y的尺寸,是一维
class LinearRegression(nn.Module):
def __init__(self,input_size,output_size):#构造函数
super(LinearRegression,self).__init__()
self.linear = nn.Linear(input_size,output_size)
def forward(self,x):#前向传播函数
out = self.linear(x)
return out
#实例化LinearRegression类
model = LinearRegression(input_size,output_size)
#第四步:定义损失函数。
# 使用均方差函数MSELoss()定义损失函数criterion,即对每个训练样本的预测值与真实值之差的平方求和。
# 需要将model的参数model.parameters()传进去
criterion = nn.MSELoss()
#第五步 定义优化函数
# 优化函数代表通过什么方式去优化需要学习值,即本例中的w和b。
#torch.optim.SGD(params, lr=)随机梯度下降算法
# params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
# lr (float) – 学习率
optimizer = t.optim.SGD(model.parameters(),lr=learning_rate)
print('optimizer',optimizer)
#第六步 训练模型
# 首次定义迭代次数,这里为1000次,先进行前向传到计算损失函数,然后进行反向传播计算梯度。
# 注:每次计算梯度前都要将梯度归零,否则梯度会累加到一起造成结果不收敛。
for epoch in range(num_epochs):
#将NumPy转成Tensor
inputs = Variable(t.from_numpy(x_train))
targets = Variable(t.from_numpy(y_train))
#前向传播
optimizer.zero_grad()
outputs = model(inputs)
#反向传播
loss = criterion(outputs,targets)
loss.backward()
#优化
optimizer.step()
#更新参数
if(epoch+1)%50 == 0:
print('Epoch[%d/%d],loss:%.4f'%(epoch+1,num_epochs,loss.item()))#原代码loss.data[0]报错,它在提醒用户下个版本这将成为一个错误
#第七步:测试模型。
model.eval()
predicted = model(Variable(t.from_numpy(x_train))).data.numpy()
plt.plot(x_train,y_train,'ro')
plt.plot(x_train,predicted,label = 'predict')
plt.legend()
plt.show()
梯度及梯度下降法
梯度
在单变量函数中,梯度就是晚熟的微分,代表函数在某个给定点上的切线的斜率
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向或反方向指明了函数在给定点上上升或下降最快的方向。
例如:函数f(x,y),分别对x,y求偏导,那么梯度向量就是(∂f/∂x,∂f/∂y),简称grad f(x,y)或▽f(x,y)
从几何角度来说,梯度其实就是函数图像变化最快的地方,沿着梯度向量的方向会更容易找到函数的最大值,相反是最小值。
因此,最小化损失函数时就可以通过梯度下降法进行不断迭代求解。
梯度下降法
将梯度下降想象成下山,寻找最快的下山路线, 每走一步思考下一步走的方向,保证下山的速度最快。挪动的步伐的大小称为学习率,步伐大,不容易找到更适合的下山方向,步伐小,速度太慢。
在深度学习中,需要寻找让损失函数值下降最多的参数组合计算损失函数,找到下降最多的参数数组,直到找到一个局部最小值。需要尝试全部的初始参数组合,才可找到不同的局部最小值。在特征较少的情况下,这种方法可能会导致算法陷入某个局部最优解。但当特征足够多时,出现的概率几乎为0。
在深度学习中有两种不同的梯度下降法,随机梯度下降法和批量梯度下降法。
(1)步长:又称学习率,决定了迭代过程中每一步沿梯度向量方向前进的长度。
(2)初始值:随机选取的初始参数组合,当损失函数是非凸函数时,可能会是局部最优解,需要多次测试,从局部解中找出全局最优解。当损失函数为凸函数时,得到的解就是全局最优解。
(3)归一化:归一化能够加快梯度下降的速度。若不进行归一化,会导致收敛的速度很慢。从而形成“之”字形的路线。
逻辑回归概述
逻辑回归实际上是分类问题。其与线性回归模型有很多相似的地方,模型形式基本相同,y = w^Tx + b其中x可以是一个多维的特征。唯一的不同点在于逻辑回归会对y作用一个逻辑函数,将其转化成概率问题。(概率问题,就像是Sigmoid函数可以将数字转化0~1区间内的数,将其分为两个类型。)
逻辑回归中的损失函数
逻辑回归使用Sigmoid函数将结果转化成0~1之间的值,对于任意一个数据点,将其经过Sigmoid函数的作用后的结果记为y^,表示这个数据点属于第二类的概率,那么属于第一类的概率为1 - y^。属于第一类的越接近于0,第二类的越接近于1。设计损失函数:
loss = -(ylog(y^) + (1-y)log(i-y^))
其中y为真实值,只能取0,1这两个值,y^ 表示逻辑回归模型的计算的 预测值 ,是一个0~1之间的值。
(1)如果y是0,表示该数据点属于第一类,希望预测值越小( 在训练模型时希望loss小,根据log函数的单调性,也就是最小化y尖。),则loss = -(log(1-y^))
(2)若y是1,表示属于第二类,希望y^大,则 loss = -(log(y^))