matlab梯度下降法_svm与梯度下降法

首先还是回顾一下原理。

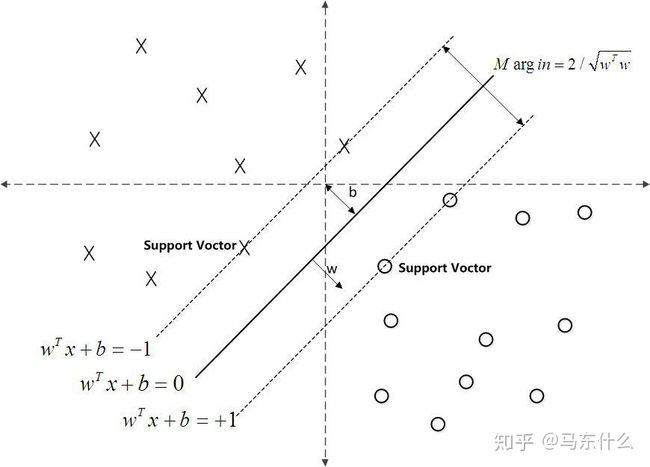
先了解一下最简单的线性svm向量机，个人认为从hinge loss的角度来解释线性svm比使用几何意义来说更加简单快速并且扩展性更好。

首先我们令：

这是一个简单的线性回归的形式，此时我们来定义损失函数：

可以看到，这是一个通用的损失函数的形式，当损失函数l为二元交叉熵的时候，上面的L(x)表示的就是逻辑回归的损失函数，当损失函数l为mse的时候，上面的L(x)表示的就是线性回归的损失函数，当l为hinge loss的时候，上面的L(x)表示的就是线性svm的损失函数。

此时我们令

,其中

为了简单起见我们令

，和逻辑回归、线性回归推导过程中的矩阵形式表达是一样的。

那么这个时候我们就可以得到线性svm的损失函数了：

，l定义如上，这称之为硬间隔线性svm的损失函数；而加入正则项之后：

,这称之为软间隔线性svm的损失函数。进一步的我们把hinge loss的表达式带入，可得（下面统一以软间隔线性svm的损失函数为例，硬间隔的推导基本类似）：

这就是线性svm的最终的损失函数，这玩意儿居然是凸函数。。。真没看出来。。。

然后就是常规的梯度下降法来求解参数了，

分别对这两个式子进行求导：

当

时，上式等于0

否则，上式等于

(这也是为什么svm要把正负样本分别定义为+1和-1的原因，如果把类别定义为0则上面这个式子的梯度永远为0)

所以，最终的梯度更新公式为：

（1）、当

时，即

时，梯度更新为0，即模型权重不进行更新。从回归的角度来说很好理解，当样本的类别为1时，用样本的特征x和权重w的乘积大小与1比较，如果大于1，表示分类正确，此样本在分界面w*x-1=0下方；当样本的类别为-1时，用样本的特征x和权重w的乘积大小与-1比较，如果小于-1，表示分类正确，此样本在分界面w*x+1=0上方。此时，svm的分类间隔为：w*x+1=0与w*x-1=0，也就是我们熟悉的图：

从上述的推导也可以看出，在分界间隔之外的样本对svm的模型来说是没有梯度贡献的，这也是为什么svm在小样本的情况下效果就可以比较好的原因，因为我们最终的分界间隔可能仅仅受少部分样本影响。

（2）、当

时，即

时，梯度更新为

,即

这样，svm的推导就完成了。

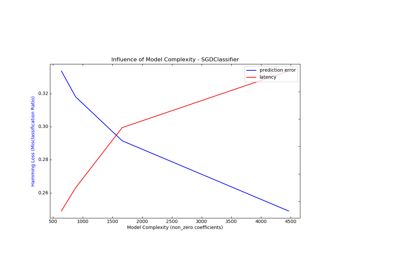
这也是sklearn中sgdclassifier的loss 为hinge的时候，svm的计算方式。

sklearn.linear_model.SGDClassifier - scikit-learn 0.21.3 documentation​scikit-learn.org

这样理解起来方便多了。

sklearn.svm.LinearSVC - scikit-learn 0.21.3 documentation​scikit-learn.org

sklearn 的linearsvc用的也是上面的求解方法，而sklearn.svm则使用的是传统的smo的求解方法，这种方法的问题难以扩展到数量巨大的样本上，而使用这种梯度下降法求解的svm则可以比较容易的扩展到海量的样本上，毕竟内存不够可以增量训练。

这就是在海量数据上使用的求解svm的pegasos算法，具体可见：

https://blog.csdn.net/sinat_27612639/article/details/70037499​blog.csdn.net

---

关于非线性svm，目前没有找到什么很准确的推导，不过在实现上倒是在sklearn的官网上发现了一个非常有意思的东西：

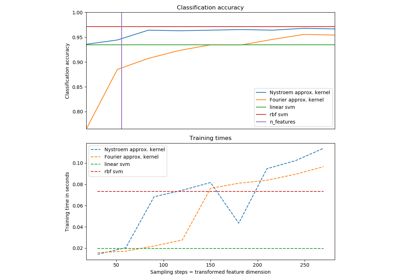
5.7. Kernel Approximation​scikit-learn.org

传统的svm的低维到高维的映射是隐式的，直接通过核技巧来规避了高维空间的复杂运算，

与隐式使用特征图的内核技巧相比，使用近似显式特征图的优势在于显式映射可以更好地适合在线学习，并且可以极大地减少使用超大型数据集的学习成本。标准的内核化SVM不能很好地适应大型数据集，但是使用近似的内核图，可以使用效率更高的线性SVM。特别是，将内核映射近似与组合 SGDClassifier可以使在大型数据集上进行非线性学习成为可能

from sklearn.kernel_approximation import RBFSampler
from sklearn.linear_model import SGDClassifier
X = [[0, 0], [1, 1], [1, 0], [0, 1]]
y = [0, 0, 1, 1]
rbf_feature = RBFSampler(gamma=1, random_state=1)
X_features = rbf_feature.fit_transform(X)
clf = SGDClassifier(max_iter=5, tol=1e-3)
clf.fit(X_features, y)

这是官方给到的一段代码，就是显式隐射然后直接上线性svm。而线性svm使用梯度下降法来求解的版本可以适用于在线学习，并且很容易并行，很容易上规模，处理大量的数据这种处理方式比较方便。

如果不是看了李宏毅的svm核技巧的讲解估计我一脸懵逼。

https://blog.csdn.net/oldmao_2001/article/details/95719629#Dual_Representation_106​blog.csdn.net

不同的核函数决定了不同的低维到高维的映射关系，而 在kernel A决定的映射关系 A下才能用kernel A实施核技巧的运算（比如你不可能用rbf核来计算原始特征空间 的多项式核的映射）。

比如：

机器学习有很多关于核函数的说法，核函数的定义和作用是什么？​www.zhihu.com

最高赞举的例子：

上述使用的多项式核函数实际上显式的映射就是把(x,y)映射为:

也就是一个二维到三维的映射。

因为原始的RBF核的映射关系实际上是映射到无穷维度的：

具体的原因可见：

https://blog.csdn.net/oldmao_2001/article/details/95719629#Dual_Representation_106​blog.csdn.net

对指数部分做了无限的泰勒展开。

sklearn.kernel_approximation.RBFSampler - scikit-learn 0.21.3 documentation​scikit-learn.org

所以sklearn中的RBFsamler做了简化，只取展开式前的N项，N可由用户自行指定。