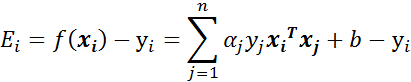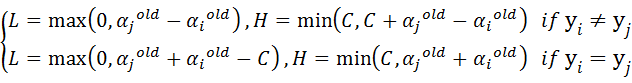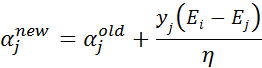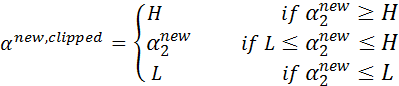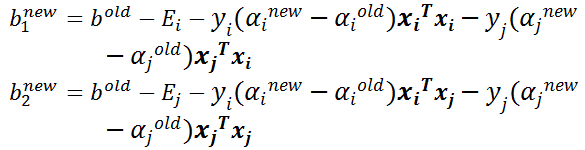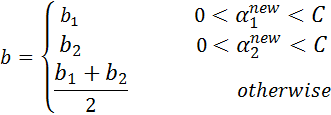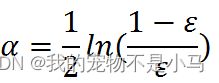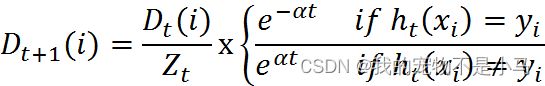机器学习实战 学习记录 （6-7章）

 参考：机器学习实战Peter Harrington

(11条消息) 机器学习实战教程(13篇)_chenyanlong_v的博客-CSDN博客_机器学习实战

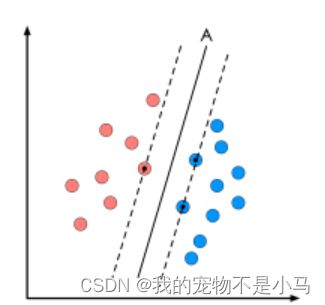
六、支持向量机 （SVM）：每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为"支持向量"。（在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置，越过该位置就会产生错分现象，如虚线所示。）

优点：泛化错误率低，计算开销不大，结果易解释

缺点：对参数调节和核函数的选择敏感，原始分类器不加修饰只适合处理二类问题

适用数据类型：数值型和标称型数据

求解这个"决策面"的过程，就是最优化。最优化问题通常有两个基本的因素：①目标函数，也就是你希望什么东西的什么指标达到最好；②优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中，目标函数显然就是那个"分类间隔"，而优化对象则是决策面。

→SMO算法：求出一系列alpha和b，一旦求出了这些alpha，就很容易计算出权重向量w并得到分隔超平面。每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha，那么就增大其中一个同时减小另一个。这里所谓的"合适"就是指两个alpha必须符合以下两个条件，条件之一就是两个alpha必须要在间隔边界之外，而且第二个条件则是这两个alpha还没有进行过区间化处理或者不在边界上。

梳理下SMO算法的步骤：

• 步骤1：计算误差：

• 步骤2：计算上下界L和H：

• 步骤3：计算η：

• 步骤4：更新αj：

• 步骤5：根据取值范围修剪αj：

• 步骤6：更新αi：

• 步骤7：更新b1和b2：

• 步骤8：根据b1和b2更新b：

示例1：简易版SMO 

ime import sleep
import matplotlib.pyplot as plt
import numpy as np
import random
import types

def loadDataSet(fileName):
    dataMat = [];labelMat = []
    fr = open(fileName)
    for line in fr.readlines(): #逐行读取，滤除空格
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])]) #添加数据
        labelMat.append(float(lineArr[2])) #添加标签
    return dataMat,labelMat

def selectJrand(i,m): #随机选择alpha，i是alpha,m是alpha参数个数
    j = i
    while(j==i): #选择一个不等于i的j
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L): #修建alpha，aj是alpha值，H是alpha上界，L是下界
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

def smoSimple(dataMatIn,classLabels,C,toler,maxIter): #C为惩罚参数，toler为松弛变量
    dataMatrix = np.mat(dataMatIn);labelMat=np.mat(classLabels).transpose() #转化为numpy的mat存储
    b = 0;m,n = np.shape(dataMatrix) #初始化参数b，统计dataMatrix的维度
    alphas=np.mat(np.zeros((m,1))) #初始化alphas参数，设为0
    iter_num = 0 #初始化迭代次数
    while(iter_num < maxIter): #最多迭代maxIter次
        alphaPairsChanged = 0 #用于记录alphas是否已经进行优化
        for i in range(m):
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b #步骤1：计算误差Ei
            Ei = fXi-float(labelMat[i])
            if((labelMat[i] * Ei < -toler)and(alphas[i] < C)) or ((labelMat[i]*Ei > toler)and(alphas[i] > 0)): #优化alpha,设置一定的容错率

                j = selectJrand(i,m) #随机选择另一个与alpha_i成对优化的alpha_j
                fXj = float(np.multiply(alphas,labelMat).T * (dataMatrix*dataMatrix[j,:].T)) + b #计算误差Ej
                Ej = fXj - float(labelMat[j])
                alphaIold=alphas[i].copy(); #保存更新前的aplpha值，使用深拷贝
                alphaJold=alphas[j].copy();
                if (labelMat[i] != labelMat[j]): #步骤2：计算上下界L和H
                    L = max(0,alphas[j] - alphas[i])
                    H = min(C,C + alphas[j]-alphas[i])
                else:
                    L = max(0,alphas[j] + alphas[i] - C)
                    H = min(C,alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                eta = 2.0 * dataMatrix[i,:] * dataMatrix[j,:].T - dataMatrix[i,:] * dataMatrix[i,:].T - dataMatrix[j,:] * dataMatrix[j,:].T #计算eta
                if eta >= 0:print("eta>=0");continue
                alphas[j] -= labelMat[j] * (Ei - Ej)/eta #步骤4：更新aj
                alphas[j] = clipAlpha(alphas[j],H,L) #步骤6：更新ai
                if (abs(alphas[j] - alphaJold) < 0.00001):print("j not moving enough");continue
                alphas[i] += labelMat[j]*labelMat[i] * (alphaJold-alphas[j])
                b1 = b - Ei - labelMat[i]*(alphas[i] - alphaIold) * dataMatrix[i,:] * dataMatrix[i,:].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i,:] * dataMatrix[j,:].T #更新b1和b2
                b2 = b - Ej - labelMat[i]*(alphas[i] - alphaJold) * dataMatrix[i,:] * dataMatrix[j,:].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j,:] * dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b=b1 #根据b1和b2更新b
                elif (0 < alphas[j]) and (C > alphas[j]): b=b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("第%d次迭代 样本：%d,alphas优化次数：%d" % (iter_num,i,alphaPairsChanged))
        if (alphaPairsChanged==0): iter_num += 1 #更新迭代次数
        else: item_num =0
        print("迭代次数：%d" % iter_num)
    return b,alphas

def showClassifer(dataMat,w,b):
    #绘制样本点
    data_plus = [] #正样本
    data_minus = [] #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus) #转化为numpy矩阵
    data_minus_np = np.array(data_minus) #转化为numpy矩阵
    plt.scatter(np.transpose(data_plus_np)[0],np.transpose(data_plus_np)[1],s=30,alpha=0.7) #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0],np.transpose(data_minus_np)[1],s=30,alpha=0.7) #负样本散点图
    #绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1,a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1,y2 = (-b - a1*x1)/a2,(-b - a1 * x2)/a2
    plt.plot([x1,x2],[y1,y2])
    #找出支持向量点
    for i,alpha in enumerate(alphas):
        if alpha > 0:
            x,y = dataMat[i]
            plt.scatter([x],[y],s=150,c='none',alpha=0.7,linewidths=1.5,edgecolor='red')
    plt.show()

def get_w(dataMat,labelMat,alphas):
    alphas,dataMat,labelMat = np.array(alphas),np.array(dataMat),np.array(labelMat)
    w = np.dot((np.tile(labelMat.reshape(1,-1).T,(1,2)) * dataMat).T,alphas)
    return w.tolist()

if __name__ == '__main__':
    dataMat,labelMat = loadDataSet('testSet.txt')
    b,alphas = smoSimple(dataMat,labelMat,0.6,0.001,40)
    w = get_w(dataMat,labelMat,alphas)
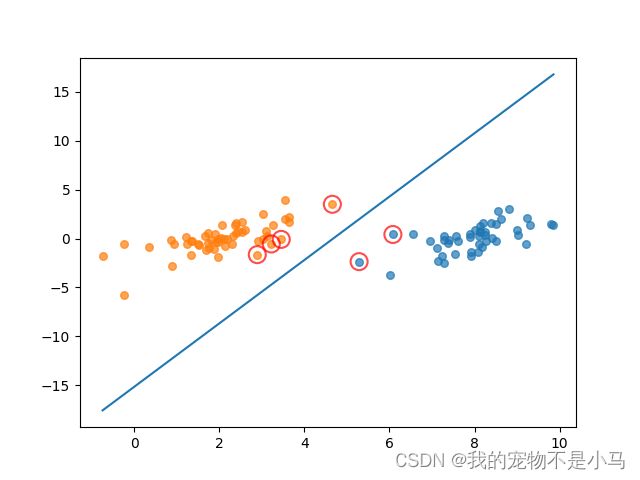
    showClassifer(dataMat,w,b)

示例2：在几百个点组成的小规模数据集上，简化版SMO算法的运行是没有什么问题的，但是在更大的数据集上的运行速度就会变慢。简化版SMO算法的第二个α的选择是随机的，针对这一问题，我们可以使用启发式选择第二个α值，来达到优化效果。 

完整Platt SMO算法是通过一个外循环来选择第一个alpha值的，并且其选择的方式会在两种方式中交替进行：一种是在所有数据集上进行单遍扫描，另一种则是在非边界的alpha中进行单遍扫描（非边界alpha即那些不等于边界0或C的alpha值）。对于整个数据集的扫描相对容易，而实现非边界alpha值的扫描时，首先需建立这些alpha值的列表，然后再对这个表进行遍历（该步骤会跳过那些已知的不会改变的alpha值。

在选择第一个alpha值之后，算法会通过第一个内循环来选择第二个alpha值。在优化过程中，会通过最大化步长的方式来获得第二个alpha值。在简化版SMO算法中，我们会在选择j之后计算错误率Ej。但在这里，我们会建立一个全局的缓存用于保存误差值，并从中选择使得步长或Ei-Ej最大的alpha值。

核函数：

七、利用AdaBoost算法提高分类性能

前面的文章已经介绍了五种不同的分类器，它们各有优缺点。我们可以很自然地将不同的分类器组合起来，而这种组合结果则被成为集成方法或者元算法。使用集成方法时会有多种形式：可以是不同算法的集成，也可以是同一种算法在不同设置下的集成，还可以是数据集不同部分分配给不同分类器之后的集成。

集成方法主要包括Bagging和Boosting两种方法，Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器，更准确的说这是一种分类算法的组装方法，即将弱分类器组装成强分类器的方法。

1.bagging（自举汇聚法）

（1）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练，（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中），共进行k轮抽取，得到k个训练集（k个训练集之间是相互独立的）。

（2）每次使用一个训练集得到一个模型，k个训练集共得到k个模型（这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法）。

（3）①对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；②对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

Bagging + 决策树 = 随机森林

2.boosting

（1）每一轮的训练数据样本赋予一个权重，并且每一轮样本的权值分布依赖上一轮的分类结果。

（2）基分类器之间采用序列式的线性加权方式进行组合。

3、Bagging、Boosting二者之间的区别

（1）样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

（2）样例权重：

Bagging：使用均匀取样，每个样例的权重相等。

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

（3）预测函数：

Bagging：所有预测函数的权重相等。

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

（4）并行计算：

Bagging：各个预测函数可以并行生成。

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

4.AdaBoost(自适应Boosting):AdaBoost算法是基于Boosting思想的机器学习算法。

优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整

缺点：对离群点敏感

适用数据类型：数值型和标称型数据

（1）计算样本权重：训练数据中的每个样本，赋予其权重，即样本权重，用向量D表示，这些权重都初始化成相等值。

（2）先在数据集上训练出一个弱分类器，①计算该分类器的错误率，错误率的定义如下：

②算法为每个分类器都分配了一个权重值alpha，alpha的定义：

 （3）权重更新：然后在同一数据集上再次训练弱数据集（重新调整每个样本的权重，其中第一次分对的样本的权重将会降低，第一次分错的样本权重将会提高）。

其中，ht(xi) = yi表示对第i个样本训练正确，不等于则表示分类错误。Zt是一个归一化因子：

不断重复训练和调整权重的过程，直到错误率为0或弱分类器的数目达到用户的指定值为止。

示例1：基于单层决策树构建弱分类器

单层决策树：它基于单个特征来做决策，只有一次分裂过程。

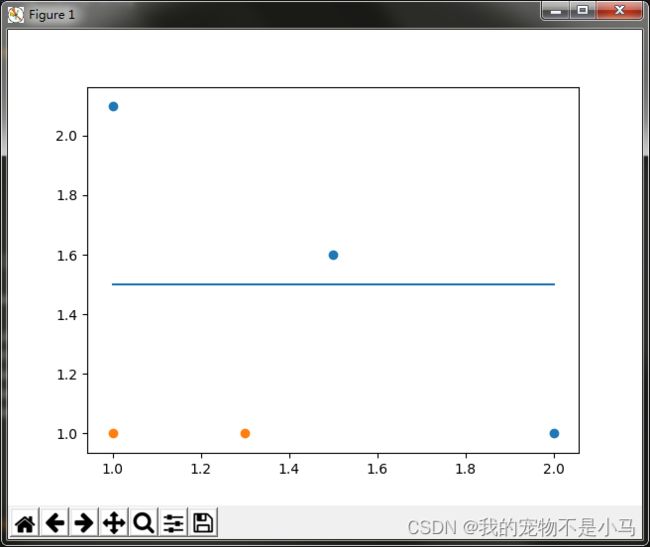
如果想要试着从某个坐标轴上选择一个值（即选择一条与坐标轴平行的直线）来将所有的蓝色圆点和橘色圆点分开，这显然是不可能的。这就是单层决策树难以处理的一个著名问题。通过使用多颗单层决策树，我们可以构建出一个能够对该数据集完全正确分类的分类器。 

蓝横线上边的是一个类别，蓝横线下边是一个类别。显然，此时有一个蓝点分类错误，计算此时的分类误差，误差为1/5 = 0.2。这个横线与坐标轴的y轴的交点，就是我们设置的阈值，通过不断改变阈值的大小，找到使单层决策树的分类误差最小的阈值。同理，竖线也是如此，找到最佳分类的阈值，就找到了最佳单层决策树。

import numpy as np
import matplotlib.pyplot as plt

def loadSimpData():
    dataMat = np.matrix([[1.,2.1],[1.5,1.6],[1.3,1.],[1.,1.],[2.,1.]])
    classLabels = [1.0,1.0,-1.0,-1.0,1.0]
    return dataMat,classLabels

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): #单层决策树分类函数
    retArray = np.ones((np.shape(dataMatrix)[0],1)) #初始化retArray为1
    if threshIneq == 'lt': #threshIneq为标志，threshVal为阈值
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 #如果小于阈值,则赋值为-1。第dim列即第几个特征
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray #返回分类结果

def buildStump(dataArr,classLabels,D): #找到数据集上最佳单层决策树，D为样本权重
    dataMatrix = np.mat(dataArr);labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0;bestStump = {};bestClasEst = np.mat(np.zeros((m,1))) #bestStump储存最佳单层决策树信息，bestClasEst为最佳分类结果
    minError = float('inf') #最小误差初始化为正无穷大
    for i in range(n): #遍历所有特征
        rangeMin = dataMatrix[:,i].min();rangeMax = dataMatrix[:,i].max(); #找到特征中最小值和最大值
        stepSize = (rangeMax - rangeMin)/numSteps #计算步长
        for j in range(-1,int(numSteps) + 1):
            for inequal in ['lt','gt']: #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize) #计算阈值
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) #计算分类结果
                errArr = np.mat(np.ones((m,1))) #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0 #分类正确的，赋值为0
                weightedError = D.T * errArr #计算误差
                print("spilt:dim %d,thresh %.2f,thresh ineqal: %s,the weighted error is %.3f" % (i,threshVal,inequal,weightedError))
                if weightedError < minError: #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    D = np.mat(np.ones((5,1))/5)
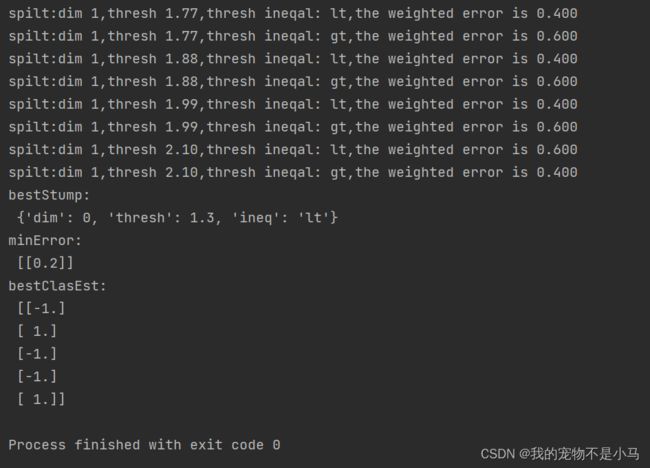
    bestStump,minError,bestClasEst = buildStump(dataArr,classLabels,D)
    print('bestStump:\n',bestStump)
    print('minError:\n',minError)
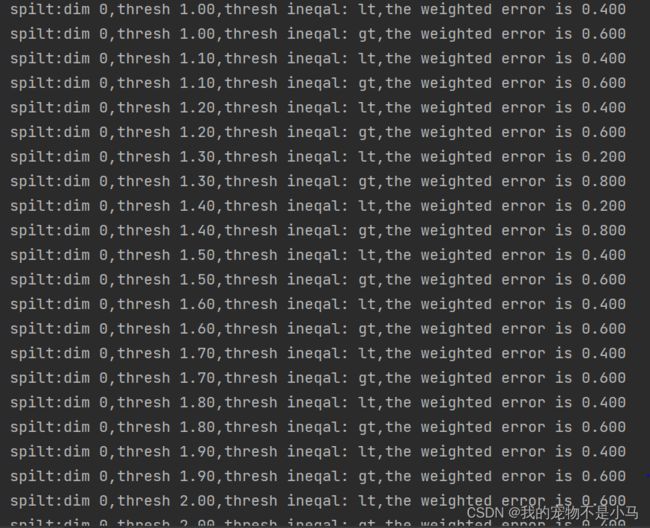
    print('bestClasEst:\n',bestClasEst)

上述程序包含两个函数。第一个函数stumpClassify()是通过阈值比较对数据进行分类的。所有在阈值一边的数据会分到类别-1，在另一边的分到类别+1。该函数通过数组过滤实现，首先将返回数组的全部元素设置为1，不满足等式要求的设置为-1。

第二个函数buildStump()会遍历stumpClassify()函数所有可能的输入值，并找到数据集上最佳单层决策树。这里的最佳是根据权重D来衡量的。

三层嵌套for循环是程序最主要的部分，第一层for循环在数据集的所有特征上遍历，考虑到数值型的特征，我们就可以通过计算最小值和最大值来了解应需要多大的步长。第二层for循环再在这些值上遍历，最后一个for循环则是在大于和小于之间切换不等式。

在循环之内，调用stumpClassify()函数返回分类预测结果。然后构建一个errArr，若predictedVals中的值不等于labelMat中真正类别标签值，则表示分类错误，errArr的值赋为1。数值weightedError为errErr和权重向量D的相应元素相乘并求和。最后将当前的错误率与已有的最小错误率进行比较，如果当前的较小，就在bestStump中保存该决策树。

 示例2：使用AdaBoost提升分类器性能

import numpy as np
import matplotlib.pyplot as plt

def loadSimpData():
    dataMat = np.matrix([[1.,2.1],[1.5,1.6],[1.3,1.],[1.,1.],[2.,1.]])
    classLabels = [1.0,1.0,-1.0,-1.0,1.0]
    return dataMat,classLabels

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): #单层决策树分类函数
    retArray = np.ones((np.shape(dataMatrix)[0],1)) #初始化retArray为1
    if threshIneq == 'lt': #threshIneq为标志，threshVal为阈值
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 #如果小于阈值,则赋值为-1。第dim列即第几个特征
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray #返回分类结果

def buildStump(dataArr,classLabels,D): #找到数据集上最佳单层决策树，D为样本权重
    dataMatrix = np.mat(dataArr);labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0;bestStump = {};bestClasEst = np.mat(np.zeros((m,1))) #bestStump储存最佳单层决策树信息，bestClasEst为最佳分类结果
    minError = float('inf') #最小误差初始化为正无穷大
    for i in range(n): #遍历所有特征
        rangeMin = dataMatrix[:,i].min();rangeMax = dataMatrix[:,i].max(); #找到特征中最小值和最大值
        stepSize = (rangeMax - rangeMin)/numSteps #计算步长
        for j in range(-1,int(numSteps) + 1):
            for inequal in ['lt','gt']: #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize) #计算阈值
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) #计算分类结果
                errArr = np.mat(np.ones((m,1))) #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0 #分类正确的，赋值为0
                weightedError = D.T * errArr #计算误差
                print("spilt:dim %d,thresh %.2f,thresh ineqal: %s,the weighted error is %.3f" % (i,threshVal,inequal,weightedError))
                if weightedError < minError: #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

def adaBoostTrainDS(dataArr,classLabels,numIt = 40):
    weakClassArr = []
    m = np.shape(dataArr)[0]
    D = np.mat(np.ones((m,1))/m) #初始化权重
    aggClassEst = np.mat(np.zeros((m,1))) #记录每个数据点的类别估计值
    for i in range(numIt):
        bestStump,error,classEst = buildStump(dataArr,classLabels,D) #构建单层决策树
        print("D:",D.T)
        alpha = float(0.5 * np.log((1.0 - error)/max(error,1e-16)))  #计算弱学习算法权重alpha,使error不等于0,因为分母不能为0
        bestStump['alpha'] = alpha #存储弱学习算法权重
        weakClassArr.append(bestStump) #存储单层决策树
        print("classEst:",classEst.T)
        expon = np.multiply(-1 * alpha * np.mat(classLabels).T,classEst) #计算e的指数项
        D = np.multiply(D,np.exp(expon))
        D = D/D.sum() #根据样本权重公式，更新样本权重
        # 计算AdaBoost误差，当误差为0的时候，退出循环
        aggClassEst += alpha * classEst
        print("aggClassEst:",aggClassEst.T)
        aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1)))
        errorRate = aggErrors.sum()/m
        print("total error:",errorRate,"\n")
        if errorRate == 0.0: break  #误差为0，退出循环
    return weakClassArr,aggClassEst

if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    weakClassArr,aggClassEst = adaBoostTrainDS(dataArr,classLabels)
    print(weakClassArr)
    print(aggClassEst)

​​​​​​​ 

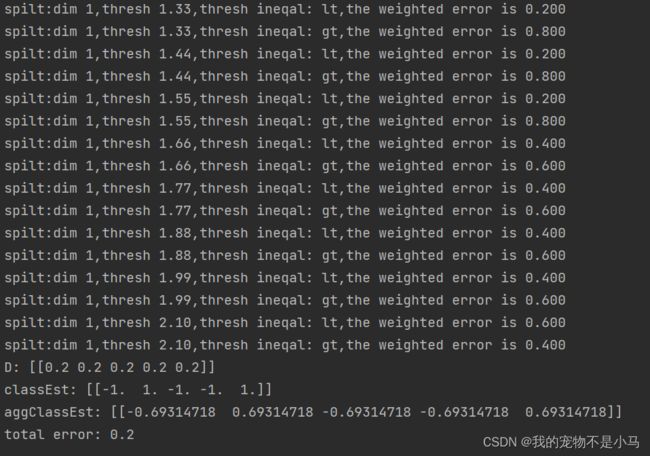
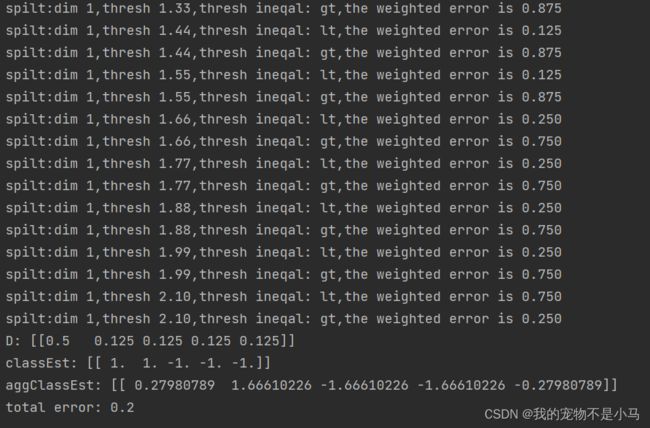
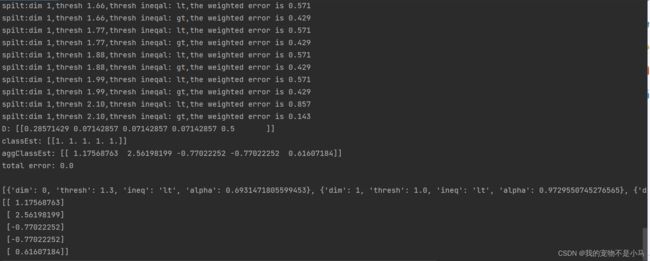
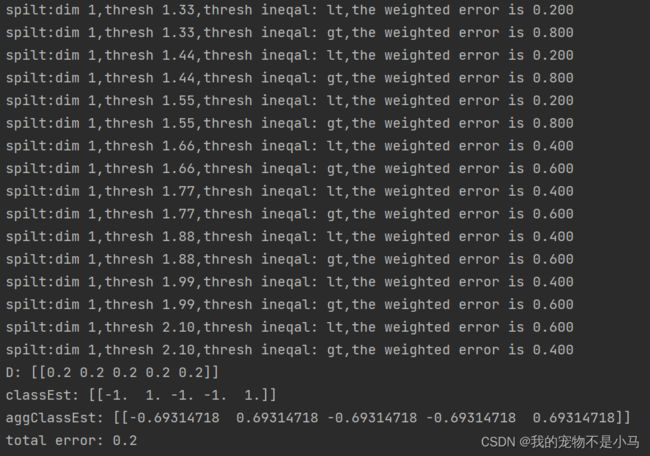
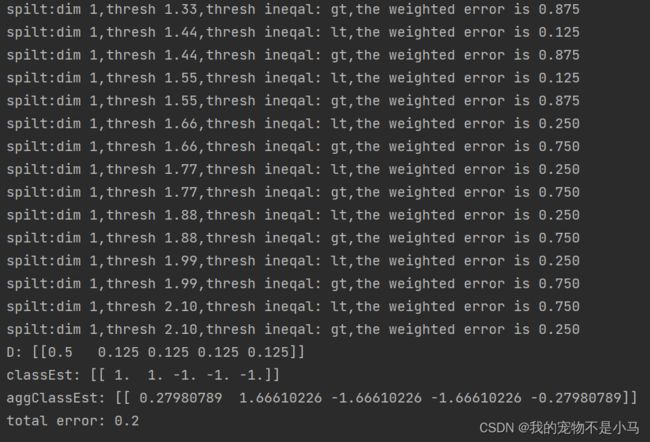
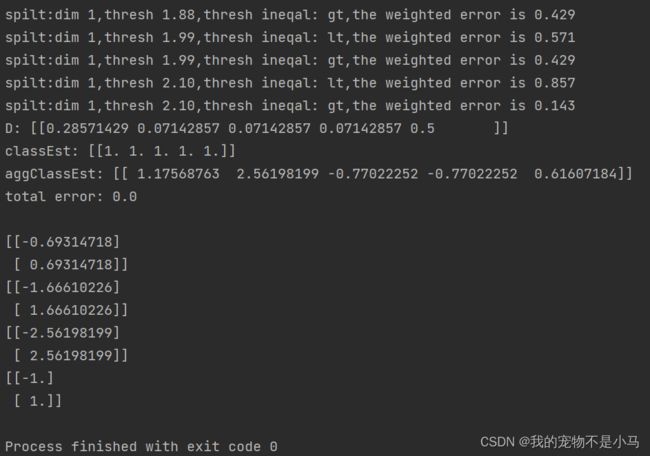
在第一轮迭代中，D中的所有值都相等。于是，只有第一个数据点被错分了。在第二轮迭代中，D向量给第一个数据点0.5的权重，第二次迭代之后，我们发现第一个数据点已经正确分类了，但此时最后一个数据点却错分了。所以在第三轮迭代中，给最后一个向量0.5的权重，第三次迭代之后aggClassEst所有值的符号和真是类别标签都完全吻合，训练错误率为0，程序终止运行。

最后训练结果包含了三个弱分类器，其中包含了分类所需要的所有信息。一共迭代了3次，所以训练了3个弱分类器构成一个使用AdaBoost算法优化过的分类器，分类器的错误率为0。 

一旦拥有了多个弱分类器以及其对应的alpha值，进行测试就变得想当容易了。

import numpy as np
import matplotlib.pyplot as plt

def loadSimpData():
    dataMat = np.matrix([[1.,2.1],[1.5,1.6],[1.3,1.],[1.,1.],[2.,1.]])
    classLabels = [1.0,1.0,-1.0,-1.0,1.0]
    return dataMat,classLabels

def showDataSet(dataMat,labelMat):
    data_plus = [] #正样本
    data_minus =[] #负样本
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus) #转化为numpy矩阵
    data_minus_np = np.array(data_minus)
    plt.scatter(np.transpose(data_plus_np)[0],np.transpose(data_plus_np)[1]) #正样本散点图
    plt.scatter(np.transpose(data_minus_np)[0],np.transpose(data_minus_np)[1]) #负样本散点图
    plt.show()

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): #单层决策树分类函数
    retArray = np.ones((np.shape(dataMatrix)[0],1)) #初始化retArray为1
    if threshIneq == 'lt': #threshIneq为标志，threshVal为阈值
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 #如果小于阈值,则赋值为-1。第dim列即第几个特征
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray #返回分类结果

def buildStump(dataArr,classLabels,D): #找到数据集上最佳单层决策树，D为样本权重
    dataMatrix = np.mat(dataArr);labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0;bestStump = {};bestClasEst = np.mat(np.zeros((m,1))) #bestStump储存最佳单层决策树信息，bestClasEst为最佳分类结果
    minError = float('inf') #最小误差初始化为正无穷大
    for i in range(n): #遍历所有特征
        rangeMin = dataMatrix[:,i].min();rangeMax = dataMatrix[:,i].max(); #找到特征中最小值和最大值
        stepSize = (rangeMax - rangeMin)/numSteps #计算步长
        for j in range(-1,int(numSteps) + 1):
            for inequal in ['lt','gt']: #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize) #计算阈值
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) #计算分类结果
                errArr = np.mat(np.ones((m,1))) #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0 #分类正确的，赋值为0
                weightedError = D.T * errArr #计算误差
                print("spilt:dim %d,thresh %.2f,thresh ineqal: %s,the weighted error is %.3f" % (i,threshVal,inequal,weightedError))
                if weightedError < minError: #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

def adaBoostTrainDS(dataArr,classLabels,numIt = 40):
    weakClassArr = []
    m = np.shape(dataArr)[0]
    D = np.mat(np.ones((m,1))/m) #初始化权重
    aggClassEst = np.mat(np.zeros((m,1))) #记录每个数据点的类别估计值
    for i in range(numIt):
        bestStump,error,classEst = buildStump(dataArr,classLabels,D) #构建单层决策树
        print("D:",D.T)
        alpha = float(0.5 * np.log((1.0 - error)/max(error,1e-16)))  #计算弱学习算法权重alpha,使error不等于0,因为分母不能为0
        bestStump['alpha'] = alpha #存储弱学习算法权重
        weakClassArr.append(bestStump) #存储单层决策树
        print("classEst:",classEst.T)
        expon = np.multiply(-1 * alpha * np.mat(classLabels).T,classEst) #计算e的指数项
        D = np.multiply(D,np.exp(expon))
        D = D/D.sum() #根据样本权重公式，更新样本权重
        # 计算AdaBoost误差，当误差为0的时候，退出循环
        aggClassEst += alpha * classEst
        print("aggClassEst:",aggClassEst.T)
        aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1)))
        errorRate = aggErrors.sum()/m
        print("total error:",errorRate,"\n")
        if errorRate == 0.0: break  #误差为0，退出循环
    return weakClassArr,aggClassEst

def adaClassify(datToClass,classifierArr): #dataToClass为待分类样例，classifierArr为训练好的分类器
    dataMatrix = np.mat(datToClass)
    m = np.shape(dataMatrix)[0] #得到待分类样例的个数m
    aggClassEst = np.mat(np.zeros((m,1)))
    for i in range(len(classifierArr)): #遍历所有分类器，进行分类
        classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],classifierArr[i]['thresh'],classifierArr[i]['ineq'])
        aggClassEst += classifierArr[i]['alpha']*classEst
        print(aggClassEst)
    return np.sign(aggClassEst)


if __name__ == '__main__':
    dataArr,classLabels = loadSimpData()
    weakClassArr,aggClassEst = adaBoostTrainDS(dataArr,classLabels)
    print(adaClassify([[0,0],[5,5]],weakClassArr))

 

 

 

通过sign函数最终的结果。可以看到，分类没有问题，(5,5)属于正类，(0,0)属于负类。 

 示例3：在一个难数据集上应用AdaBoost

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))
    dataMat = [];labelMat =[]
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat-1):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): #单层决策树分类函数
    retArray = np.ones((np.shape(dataMatrix)[0],1)) #初始化retArray为1
    if threshIneq == 'lt': #threshIneq为标志，threshVal为阈值
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 #如果小于阈值,则赋值为-1。第dim列即第几个特征
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray #返回分类结果

def buildStump(dataArr,classLabels,D): #找到数据集上最佳单层决策树，D为样本权重
    dataMatrix = np.mat(dataArr);labelMat = np.mat(classLabels).T
    m,n = np.shape(dataMatrix)
    numSteps = 10.0;bestStump = {};bestClasEst = np.mat(np.zeros((m,1))) #bestStump储存最佳单层决策树信息，bestClasEst为最佳分类结果
    minError = float('inf') #最小误差初始化为正无穷大
    for i in range(n): #遍历所有特征
        rangeMin = dataMatrix[:,i].min();rangeMax = dataMatrix[:,i].max(); #找到特征中最小值和最大值
        stepSize = (rangeMax - rangeMin)/numSteps #计算步长
        for j in range(-1,int(numSteps) + 1):
            for inequal in ['lt','gt']: #大于和小于的情况，均遍历。lt:less than，gt:greater than
                threshVal = (rangeMin + float(j) * stepSize) #计算阈值
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) #计算分类结果
                errArr = np.mat(np.ones((m,1))) #初始化误差矩阵
                errArr[predictedVals == labelMat] = 0 #分类正确的，赋值为0
                weightedError = D.T * errArr #计算误差
                print("spilt:dim %d,thresh %.2f,thresh ineqal: %s,the weighted error is %.3f" % (i,threshVal,inequal,weightedError))
                if weightedError < minError: #找到误差最小的分类方式
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

def adaBoostTrainDS(dataArr,classLabels,numIt = 40):
    weakClassArr = []
    m = np.shape(dataArr)[0]
    D = np.mat(np.ones((m,1))/m) #初始化权重
    aggClassEst = np.mat(np.zeros((m,1))) #记录每个数据点的类别估计值
    for i in range(numIt):
        bestStump,error,classEst = buildStump(dataArr,classLabels,D) #构建单层决策树
        print("D:",D.T)
        alpha = float(0.5 * np.log((1.0 - error)/max(error,1e-16)))  #计算弱学习算法权重alpha,使error不等于0,因为分母不能为0
        bestStump['alpha'] = alpha #存储弱学习算法权重
        weakClassArr.append(bestStump) #存储单层决策树
        print("classEst:",classEst.T)
        expon = np.multiply(-1 * alpha * np.mat(classLabels).T,classEst) #计算e的指数项
        D = np.multiply(D,np.exp(expon))
        D = D/D.sum() #根据样本权重公式，更新样本权重
        # 计算AdaBoost误差，当误差为0的时候，退出循环
        aggClassEst += alpha * classEst
        print("aggClassEst:",aggClassEst.T)
        aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1)))
        errorRate = aggErrors.sum()/m
        print("total error:",errorRate,"\n")
        if errorRate == 0.0: break  #误差为0，退出循环
    return weakClassArr,aggClassEst

def adaClassify(datToClass,classifierArr): #dataToClass为待分类样例，classifierArr为训练好的分类器
    dataMatrix = np.mat(datToClass)
    m = np.shape(dataMatrix)[0] #得到待分类样例的个数m
    aggClassEst = np.mat(np.zeros((m,1)))
    for i in range(len(classifierArr)): #遍历所有分类器，进行分类
        classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],classifierArr[i]['thresh'],classifierArr[i]['ineq'])
        aggClassEst += classifierArr[i]['alpha']*classEst
        print(aggClassEst)
    return np.sign(aggClassEst)


if __name__ == '__main__':
    dataArr,LabelArr = loadDataSet('horseColicTraining2.txt')
    weakClassArr,aggClassEst = adaBoostTrainDS(dataArr,LabelArr)
    testArr,testLabelArr = loadDataSet('horseColicTest2.txt')
    print(weakClassArr)
    predictions = adaClassify(dataArr,weakClassArr)
    errArr = np.mat(np.ones((len(dataArr),1)))
    print('训练集的错误率：%.3f%%' % float(errArr[predictions != np.mat(LabelArr).T].sum()/len(dataArr) * 100))
    predictions = adaClassify(testArr,weakClassArr)
    errArr = np.mat(np.ones((len(testArr),1)))
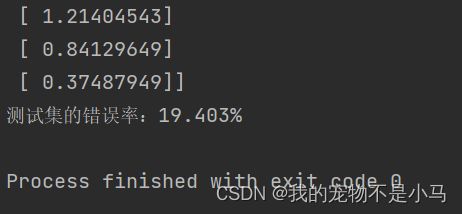
    print('测试集的错误率：%.3f%%' % float(errArr[predictions != np.mat(testLabelArr).T].sum()/len(testArr) * 100))

 

训练集错误率未显示。

 5.非均衡问题

至此，本书都是基于错误率来衡量分类器任务的成功程度的，这样的度量错误掩盖了样例如何被分错的事实。

（1）

正确率 ：TP/(TP+FP)，预测为正例的样本中真正正例的比例

召回率：TP/(TP+FN),预测为正例的真实正例占所有真实正例的比例

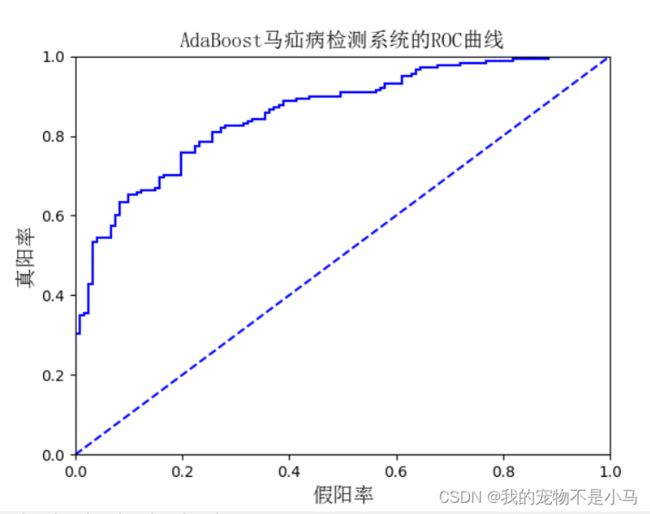
（2）ROC曲线 

图中的横坐标是伪正例的比例（假阳率=FP/（FP+TN）），而纵坐标是真正例的比例（真阳率=TP/（TP+FN））。ROC曲线给出的是当阈值变化时假阳率和真阳率的变化情况。左下角的点所对应的将所有样例判为反例的情况，而右上角的点对应的则是将所有样例判为正例的情况。虚线给出的是随机猜测的结果曲线。 

在理想的情况下，最佳的分类器应该尽可能地处于左上角，这就意味着分类器在假阳率很低的同时获得了很高的真阳率。

对不同的ROC曲线进行比较的一个指标是曲线下的面积（Area Unser the Curve，AUC）。AUC给出的是分类器的平均性能值，当然它并不能完全代替对整条曲线的观察。一个完美分类器的ACU为1.0，而随机猜测的AUC则为0.5。

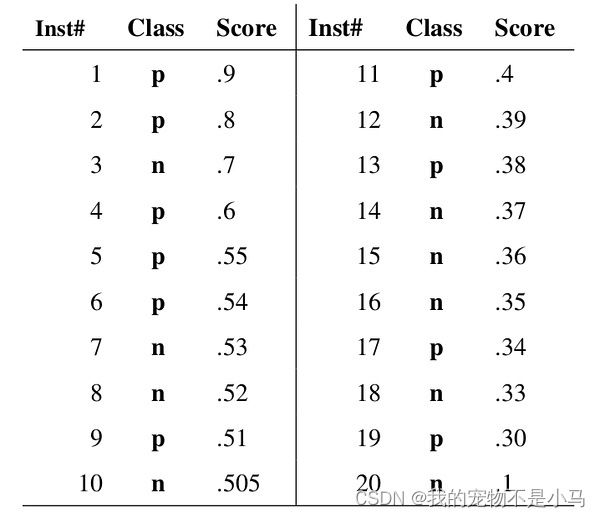
→ROC曲线原理：

 

• 当阈值为0.9时，样本1的“Score”值为0.9，大于等于阈值，那么样本1为正类，其余为负类，则TPR=TP/（TP+FN）=1/10=0.1，FPR=FP/（FP+TN）=0/10=0；
• 当阈值为0.8时，样本1的“Score”值为0.9，样本2的“Score”值为0.8，大于等于阈值，那么样本1，2为正类，其余为负类，则TPR=2/10=0.2，FPR=0/10=0；
• 当阈值为0.7时，样本1，2，3的"Score"值大于等于阈值，那么样本1，2，3为正类，其余为负类，则TPR=2/10=0.2，FPR=1/10=0.1；
• 当阈值为0.6时，样本1，2，3，4的"Score"值大于等于阈值，那么样本1，2，3，4为正类，其余为负类，则TPR=3/10=0.3，FPR=1/10=0.1；

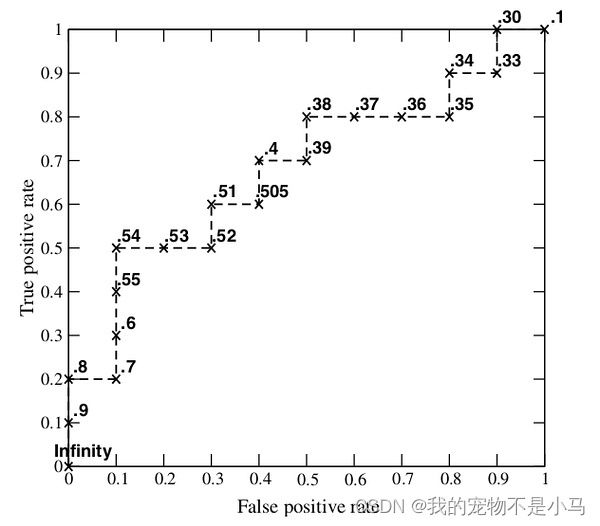
结果如下图： 

 

ROC越靠拢于左上角，分类器性能越好。同理AUC越接近于1，分类器性能越好。 

（3）处理非均衡问题的数据抽样问题：对分类器的训练数据进行改造，可以通过欠抽样（删除样例）或过抽样（复制样例）来实现。