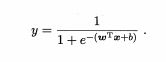机器学习面试——逻辑回归和线性回归
1、什么是广义线性模型（generalize linear model）？
普通线性回归模型是假设X为自变量，Y为因变量，当X是一维的，y是一维的，共进行n次观测，则
其中，w是待估计的参数，称为回归系数，b是随机误差（统计学相关书籍会写
）,服从正态分布，称该模型为一元线性回归。当X为多维时，y是一维，称模型是多元线性回归，公式为
因为b是服从正态分布的，重要假设：因变量也服从正态分布。
广义线性模型是做了两点补充，一是因变量不一定是服从正态分布，而是推广到一个指数分布族（包含正态分布、二项分布、泊松分布等）；二是引入联接函数g，g满足单调，可导，自变量和因变量通过联接函数进行关联。常见联接函数有对数函数、幂函数，平方根等。
Logits 回归就是广义线性模型，随机误差项服从二项分布。
2、介绍LR（线性回归），原理推导
线性回归的推导通常有两种方式：正规方程求解，梯度下降法
线性模型：
均方误差是求解线性回归的评估指标，则损失函数为均方损失，公式为
求解偏导数：
最终化简为
局部加权线性回归：为解决欠拟合问题，通过核方法进行局部加权。
当特征比样本数量多时，输入数据X矩阵的逆可能不存在，因此引入正则化。
Lasso回归：引入L1正则化项，L1比L2更稀疏，目标函数为
Ridge回归：引入L2正则化项
3、介绍LR（逻辑回归），原理推导
概念：
几率：是指一个事件发生的概率和该事件不发生的概率比值。
线性模型是可以进行回归学习的，常见的模型是线性回归，但是如果进行分类任务呢？找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。考虑到二分类，其输出标记是[0,1],可以将线性模型的预测值转换为0或1，首先考虑单位阶跃函数
但是单位阶跃函数不连续，可以考虑换一个近似单位阶跃函数的替代函数，并单调可微，则考虑对数几率函数（sigmoid函数），将预测值转换为接近0,1的值
经过函数变形，可得：
称
为几率，反映了x作为正例的相对可能性，
为对数几率（logit），在用线性回归模型的预测结果去逼近 真实标记的对数几率，因此，其对应的模型称为"对数几率回归" (logistic regression ，亦称 逻辑回归) 。
因为y只取0,1，则条件概率分布如下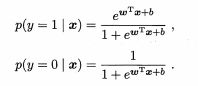
，假设
=h(z)，则
=1-h(z)，可以通过极大似然估计来求解w,b。
似然函数为：![\prod \left [h(z)) \right ]^{y_{i}}\left [1-h(z)) \right ]^{1-y_{i}}](http://img.e-com-net.com/image/info8/1a3756f8554844c5aaf2fb669386523c.gif){kind=small}
,其中，
,
，解释z是可以转换为,将b值加入到矩阵中，一下计算
对数化，求得对数似然函数，问题变成了以对数似然函数为目标函数的最优化问题：
。
对数似然函数进行求偏导（链式法则），
组合为：
优化策略：梯度下降法、牛顿法
每次迭代对参数进行更新：
梯度下降法(一阶导信息)：
，
是步长。
牛顿法（二阶到信息）：
4、常见优化算法？
梯度下降法：分为随机梯度下降，批量梯度下降，mini-batch梯度下降
随机梯度下降：局部最优解，随机选取样本进行优化，收敛速度慢，不支持并行
批量梯度下降：一次迭代，对所有样本进行计算，当函数时凸函数时，容易求得最小值，但是收敛速度较慢。
mini-batch梯度下降：是随机梯度下降和批量梯度下降的折中，
牛顿法：在迭代时，需要计算Hessian矩阵，当维度较高时，计算Hessian矩阵较困难。
拟牛顿法：不用二阶偏导数而构造出可以近似海塞矩阵（或海塞矩阵的逆）的正定对称阵。
5、介绍一下L0,L1,L2
模型选择的典型方法是正则化，正则化是结构风险最小化策略的实现，在经验风险后边加一个正则化项或罚项。正则化的作用就是选择经验风险与模型复杂度同时较小的模型。常见的正则化方式有：
L0:是指向量中非0的元素的个数
L1:先验服从拉普拉斯分布，是向量各个元素的绝对值之和，可以使得学习得参数具有稀疏性。
L2:先验服从高斯分布，是向量各个元素的平方和的1/2方，防止模型过拟合。
6、逻辑回归和线性回归的区别和联系？
联系：都是线性模型，在求解超参数时，都可以使用梯度下降等优化方法
区别：
- 逻辑回归是解决分类问题，线性回归解决回归问题，即逻辑回归的因变量是离散值，线性回归的因变量是连续值
- 逻辑回归是用极大似然估计建模（交叉熵损失函数），线性回归是最小二乘法（均方误差）
- 逻辑回归是假设y服从0-1分布，线性回归假设y服从正态分布
7、逻辑回归和SVM对比
联系：都是线性模型
区别：
LR的损失函数是交叉熵损失函数，SVM是合页损失函数（hinge loss）
SVM只考虑支持向量，需要样本数较少。
8、LR的优缺点
优点： 1）速度快。 2）简单易于理解，直接看到各个特征的权重。 3）能容易地更新模型吸收新的数据。 4）如果想要一个概率框架，动态调整分类阀值。
缺点： 特征处理复杂。需要归一化和较多的特征工程
4、比较LR和GBDT？
(1) LR是一种线性模型，而GBDT是一种非线性的树模型，因此通常为了增强模型的非线性表达能力，使用LR模型之前会有非常繁重的特征工程任务；
(2) LR是单模，而GBDT是集成模型，通常来说，在数据低噪的情况下，GBDT的效果都会优于LR；
(3) LR采用梯度下降方法进行训练，需要对特征进行归一化操作，而GBDT在训练的过程中基于gini系数选择特征，计算最优的特征值切分点，可以不用做特征归一化。