每日一课 | 详解数据分析中违背常理的悖论:辛普森悖论
Python大本营每日一课
大家好,本期7日专栏内容,营长将为大家分享新的内容知识,“数据分析”,营长邀请的是宿永杰,某知名互联网公司数据挖掘工程师,小伙伴们别忘记打卡哦。
数据分析中违背常理的悖论:辛普森悖论
DAY03
上期我们分享了每日一课 | 详解数据分析最爱用的估算法,不清楚的小伙伴可以点击查看详情哦!
在现实生活中,我们常常会遇到这样一种现象,当尝试研究两个变量是否具有相关性的时候,会分别对此进行分组研究。
然而,在分组比较中都显示非常有优势的一方,在总评时却成了失势的一方。直到 1951 年,英国统计学家 E.H.辛普森发表论文对此现象做了描述解释,后来人们就以他的名字命名该现象,即辛普森悖论。
思考下,辛普森悖论为什么成立?
辛普森悖论的原理
下面给出辛普森悖论的数学原理:
从数学表达式上,我们可以看出,对 a、b、c、d 四个变量,分成 1 组和 2 组,在 1 组比率占优势的情况下,总体占优势却不成立。
看一个例子:抖音 6 月与 7 月活跃人群得活跃时长对比,发现男性活跃时长上升,女性也上升,但是整体上 7 月活跃时长比 6 月降低是什么原因?
从数学表达式上,我们可以看出,对 a、b、c、d 四个变量,分成 1 组和 2 组,在 1 组比率占优势的情况下,总体占优势却不成立。
看一个例子:抖音 6 月与 7 月活跃人群得活跃时长对比,发现男性活跃时长上升,女性也上升,但是整体上 7 月活跃时长比 6 月降低是什么原因?
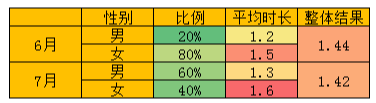
为了让结果更直观,我做了一个数据图,不是很标准,但是足以解释。
假设 6 月,活跃男生占比 20%,使用平均时长 1.2h;活跃女生占比 80%,使用平均时长 1.5h,则可以计算 6 月整体使用时长为 1.44h。同理,假设 7 月,活跃男生占比 60%,使用平均时长 1.3h;活跃女生占比 40%,使用平均时长 1.6h,则可以计算 7 月整体使用时长为 1.42h。
这样就可以非常清晰地看出,7 月比 6 月男女生的平均观看时长确实增加了,但是整体的反而降低,问题出现在活跃男女生的比例上。
所以,上述抖音案例的解释,应该是 6 月活跃人群女性占比较大,而七月男生占比较大,虽然 7 月男女生观看时长都增长了,但是由于一天 24 小时,除掉工作吃饭睡觉时间,男女生活跃时长的提升幅度并不是很大,这样就导致,虽然 7 月男女生活跃观看时长都有提升,但是整体 7 月的活跃时长低于 6 月,本质还是活跃人群结构男女比例发生变化。
所以在运营的时候,在活跃时长增长幅度有限的条件下,如果想增加整体的时长,先保证人群结构中女生占较大比例,再引导男女行增长活跃时长。
如何避免出现辛普森悖论
关于如何避免出现辛普森悖论,我个人觉得,辛普森悖论无法完全避免的,很多问题,完全依靠统计学推导因果关系无法实现。就拿生产环境数据来说,虽然我们做了各种画像,但是其他分类方式依然存在,理论上的潜在变量会无穷无尽。
我们能做的,就是仔细认真地研究各种影响因素,不要笼统概括地看问题,尤其数据分析问题,拆解得越细,最终得到的效果越好。
关于避免辛普森悖论的出现,目前比较流行的一种做法,就是需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必须了解该情境是否存在其他潜在因素,需要进行综合性考虑。
这段话看完有点晕圈,在实际中斟酌权重和判断其他因素,大多数还是更多依赖经验。
虽然不能根本上避免辛普森悖论,但我们至少应该明白:在因果关系里,量与质是不等价的,但是量比质更容易测量,所以人们总是习惯用量来评定好坏,而该数据却不是重要的。
倒过来说辛普森悖论
前面讲的辛普森悖论是:在每个分组中占优势的一方,但整体总评却成了失势的一方。那倒过来说辛普森悖论,就是在总体中占优势的一方,在每个分组比较中反而都占劣势。
下面介绍一个案例,假设,某产品的推广渠道有头条和微信两种,头条整体的付费转化率是 3.1%,微信整体的付费转化率是 1.38%,连头条转化率的一半都不到。于是有数据分析师得出结论:微信用户付费转化率较低,建议停止微信端的广告投放。
你认为这个分析师做的对吗?
我们先来看看,头条和微信整体转化率对比情况,头条的确实比微信转化率要高:
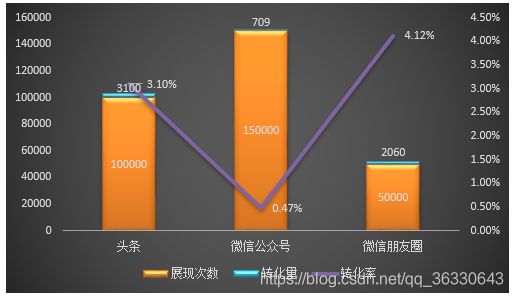
但是,正常情况下,微信的广告包括微信公众号和微信朋友圈两部分,我们把微信的数据量拆开来对比:
这里,我们会惊奇地发现,原来朋友圈的转化率是最高的 4.12%,而微信公众号的转化率很低,但是展示量很大,把整个微信的值拉低了。也可以说,那个分析师失误了,误区产生的原因就在于将“值与量”两个维度的数据,归纳成了“值”一个维度的数据,并进行了合并。
如果要避免“辛普森悖论”给我们带来的误区,就需要斟酌个别分组的权重,以一定的系数去消除因分组资料基数差异所造成的影响。
而在实际工作中,就需要尽量去拆解指标,采用 MECE 原则,指标维度互不重复,完全穷尽。
内容延伸
我们继续理解一个概念:基本比率谬误(base rate fallacy)。
先看一个例子,小易生病去医院,做完检查结果呈阳性,医生告诉他可能是患上了 XX 疾病,吓得他惊慌失措,冷静之余,他赶忙到网上查询资料,网上说检查总是有误差的,这种检查有“百分之一的假阳性率和百分之一的假阴性率”。
这句话的意思是说,在得病的人中做实验,有 1% 的人是假阳性,99% 的人是真阳性。而在未得病的人中做实验,有 1% 的人是假阴性,99% 的人是真阴性。
于是,小易根据这种解释,估计他自己得了 XX 疾病的可能性(即概率)为 99%。可是,医生却告诉他,他被感染的概率只有 0.09 左右。这是怎么回事呢?
医生说:你忘了一件事,XX 病在人口中的得病基本比例(1/1000)这个事实。
医生给出计算方法:因为测试的误报率是 1%,1000 个人将有 10 个被报为“假阳性”,而根据 X 病在人口中的比例(1/1000=0.1%),真阳性只有 1 个。所以,大约 11 个测试为阳性的人中只有一个是真阳性(有病)的,因此,小易被感染的几率是大约 1/11,即 0.09(9%)。
基本比率谬误数学解释,首先要回顾下贝叶斯定理:
P(A|B) = \frac{P(B|A)}{P(B)}P(A)
P(A∣B)=P(B)
P(B∣A)
P(A)
从贝叶斯定理的原理,解释小易被感染的几率就计较容易了。
A:普通人群中的小易感染 XX 病
B:阳性结果
P(A):普通人群中感染 X 病的概率
P(B|A):阳性结果的概率
P(A|B):有了阳性结果条件下,小易感染 XX 病的概率
P(B):结果为阳性的总可能性 = 检查阳性中的真阳性 + 检查阴性中的真阳性
类似的悖论,还有罗杰斯现象、伯克森悖论、生日悖论等。
总结
本文介绍了数据分析容易犯的一个误区,辛普森悖论。上面的例子也告诉我们,统计学中有不少陷阱,如果不提前进行了解,工作中很可能会被错误的统计方法迷惑,得出不正确的结论。
辛普森悖论让我们明白了,在因果关系里,量与质是不等价的,但是量比质更容易测量,所以人们总是习惯用量来评定好坏,而该数据却不是重要的。
辛普森悖论带给我们的另外一个启示是:如果我们在人生的抉择上选择了一条比较难走的路,就得具备可能不被赏识、怀才不遇的心理准备。
明日分享预告:数据分析的本质是什么?
本期专栏内容均来自GitChat《数据分析面试剖析24讲》专栏内容,作者:宿永杰,某著名互联网公司数据挖掘工程师,如需了解专栏详情,可扫描下方二维码。