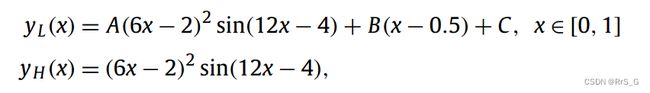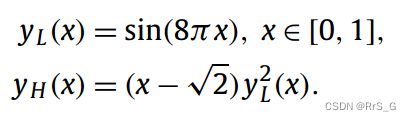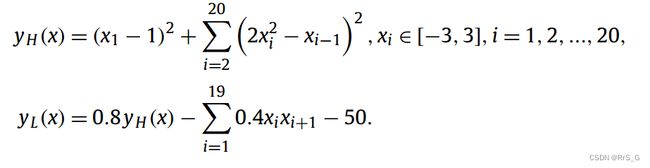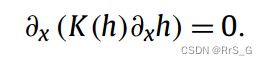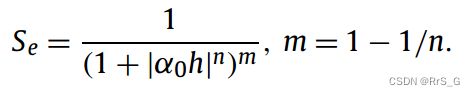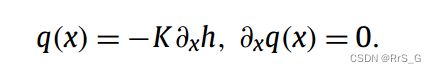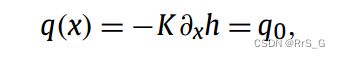A composite neural network that learns from multi-fidelitydata: Application to function approximati
目录
一、背景
二、多保真DNN和多保真PINN
三、各类问题
3.1. 函数逼近
3.1.1. 具有线性相关的连续函数
3.1.2. 具有非线性相关的连续函数
3.1.3. 20维函数的近似
3.2. 非线性反偏微分方程问题
3.2.1. 学习非饱和非线性流动的水力导率
四、前景
一、背景
深度学习的快速发展也影响了物理系统的计算建模。通常,复杂物理系统的优化需要大量的高保真数据集,这可能会导致计算成本过高。另一方面,不充分的高保真数据会导致不准确的近似和可能错误的设计。多保真建模已经被证明是高效和有效的,通过利用低保真和高保真数据在不同的应用中实现高精度。在多保真度建模框架中,精确但昂贵的高保真度数据是稀缺的,而廉价且不准确的低保真度数据是丰富的。在很多情况下,低保真数据可以为高保真数据提供有关趋势的有用信息,因此,基于少量高保真数据的多保真建模可以大大提高单保真数据的预测精度。
在多保真度方法中,构建低保真度和高保真度数据之间的相互关系是至关重要的。在现有的方法中,高斯过程回归(GPR)结合线性自回归格式得到了广泛的应用,受到了广泛的关注。但是具有线性自回归格式的高斯过程回归只能捕获低保真度和高保真度数据之间的线性相关性。也有人扩展了该方法,使其能够学习复杂非线性相关。虽然已经取得了很大的进展,但基于GPR的多保真方法仍有一些局限性,如不连续函数的逼近、高维问题、强非线性反问题(即非线性偏微分方程)。此外,GPR的优化实现起来也相当困难。因此,迫切需要克服这些缺陷的多保真方法。
深度神经网络可以在低维和高维中轻松处理几乎任何非线性问题。此外,最近提出的PINN已经显示出学习具有非线性的逆PDE问题中的未知参数或函数的能力。尽管PINN具有强大的表达能力,但在非线性偏微分方程中识别未知参数需要大量的高保真数据,这样的数据很难获得。
本文充分利用深度神经网络(DNNs)的优点和多保真建模的概念,提出开发多保真DNNs和多保真PINNs (MPINNs),它们具有以下吸引人的特点:(1)它们可以自适应地学习线性和非线性相关;(2)它们适用于高维问题;(3)能处理强非线性逆问题;(4)它们易于实现,正如在本工作中所证明的。
二、多保真DNN和多保真PINN
多保真度建模的关键出发点是发现和利用低保真度数据和高保真度数据之间的关系。广泛使用的综合关联表示为
![]() (1)
(1)
其中![]() 和
和![]() 分别为低保真度数据和高保真度数据。
分别为低保真度数据和高保真度数据。
很明显,基于这种关系的多保真模型只能处理两保真数据之间的线性相关。所以为了获取非线性相关性,本文提出了一种广义自回归格式,表示为
![]() (2)
(2)
其中F(.)是未知(线性/非线性)函数,将低保真数据映射到高保真水平。等式(2)可以进一步写为
![]() (3)
(3)
为了自适应探究线性/非线性的相关性,将![]() 分解为两部分,即线性部分和非线性部分,分别表示为
分解为两部分,即线性部分和非线性部分,分别表示为
![]() , (4)
, (4)
然后,相关性构建为
![]() (5)
(5)
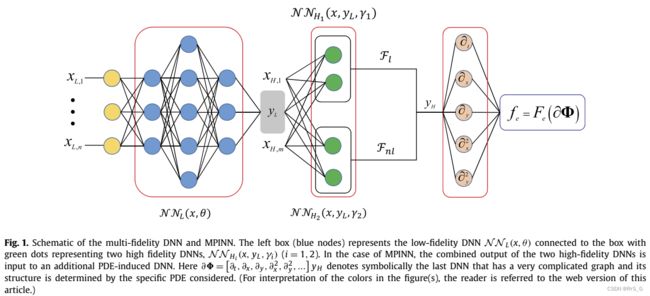
提出的多保真DNN和MPINN的架构如图1所示,由四个全连接神经网络组成。
第一个网络是为了近似低保真数据,第二个和第三个网络是为了近似低保真和高保真数据的相关性,最后一个网络是为了编码偏微分方程。
另外,![]() ,
,![]() ,
,![]() 是网络的参数,可以通过最小化下面的损失来学习:
是网络的参数,可以通过最小化下面的损失来学习:
带*的是对应网络的输出,β是![]() 和
和![]() 中的权重,λ是β的L2正则化速率。这里使用L2正则化来减少
中的权重,λ是β的L2正则化速率。这里使用L2正则化来减少![]() 和
和![]() 的过拟合。另外,如果有低保真数据的梯度,还可以惩罚
的过拟合。另外,如果有低保真数据的梯度,还可以惩罚![]() ,这有助于
,这有助于![]() 的逼近。值得一提的是,fe的边界/初始条件也可以添加到损失函数中,类似于PINN。
的逼近。值得一提的是,fe的边界/初始条件也可以添加到损失函数中,类似于PINN。
最后,解释一下式(5)中线性/非线性分解背后的基本原理。一般来说没有关于低保真度数据和高保真度数据之间的相关性的先验知识,这需要基于给定的数据来学习。在非线性相关情况下,![]() 的训练损失要比
的训练损失要比![]() 小得多,这使得本方法更倾向于非线性相关。通过对
小得多,这使得本方法更倾向于非线性相关。通过对![]() 进行正则化,多保真度的DNN趋于低保真度数据与高保真度数据之间的线性相关。因此,现有的多保真度框架可以自适应地探索线性/非线性相关性。
进行正则化,多保真度的DNN趋于低保真度数据与高保真度数据之间的线性相关。因此,现有的多保真度框架可以自适应地探索线性/非线性相关性。
三、各类问题
接下来将介绍多保真度DNN和MPINN的几个测试,MPINN主要是在与地球物理应用相关的两个PDE反问题的背景下进行的。
3.1. 函数逼近
3.1.1. 具有线性相关的连续函数
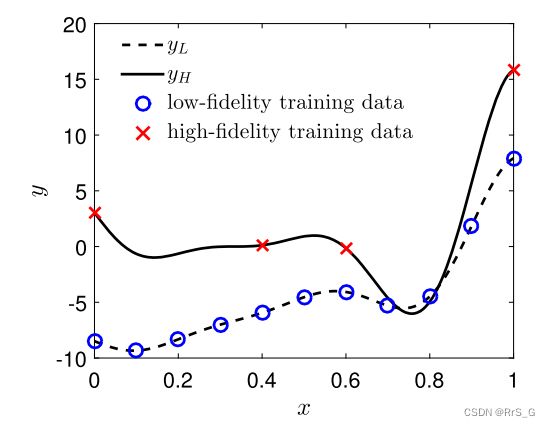
考虑一个例子,低保真度数据和高保真度数据由下式产生:
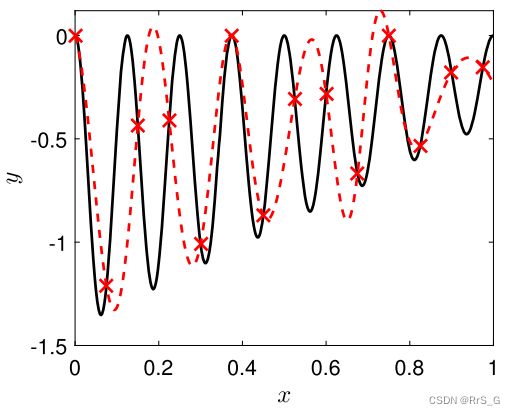
首先尝试只用高保真数据来逼近函数。这种情况,只需要保留![]() ,而且它的输入只有x,并且没有正则化。结果如下:
,而且它的输入只有x,并且没有正则化。结果如下:
由于缺乏足够的高保真数据,所以预测结果不准确。
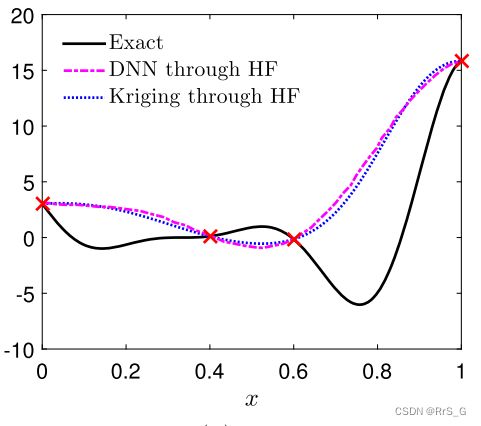
现在加入低保真数据,这里用到的网络就是图1中除去最后一层的部分。结果如下:
红色虚线为本文模型,蓝点是本文模型去除掉![]() ,品红虚线为Co-Kriging[7]。
,品红虚线为Co-Kriging[7]。
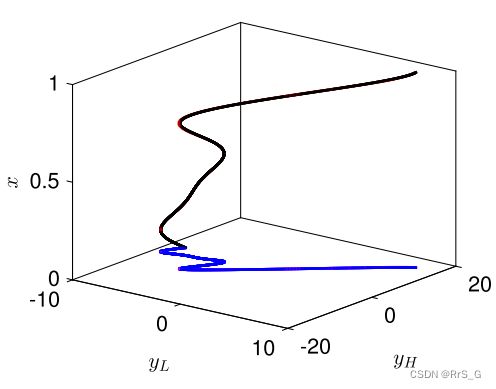
最后,估计的相关性如下图所示:
(x, yL, yH)平面中的红色虚线表示Eq.(5)(在确切的黑色实线之上),(yL, yH)平面中的红色虚线表示高保真度和低保真度数据之间的相关性。
可以看出和准确的结果非常吻合,而且与Co-Kriging不同,多保真度DNN不需要高保真度和低保真度数据之间的相关性先验知识,这表明本模型可以基于给定的数据动态学习相关性。
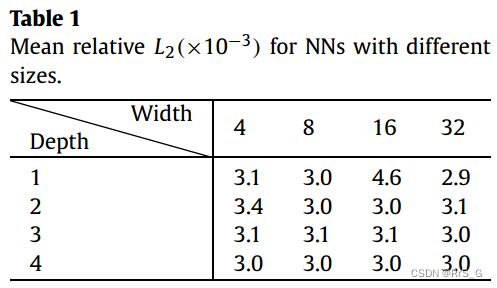
作者还根据网络![]() 的深度和宽度做了对比实验:
的深度和宽度做了对比实验:
可以看出误差很小而且都差不多。这些结果都证明了多保真度DNN的鲁棒性。
3.1.2. 具有非线性相关的连续函数
为了检验本模型在低保真度和高保真度数据之间的复杂非线性关联,进一步考虑以下情况:
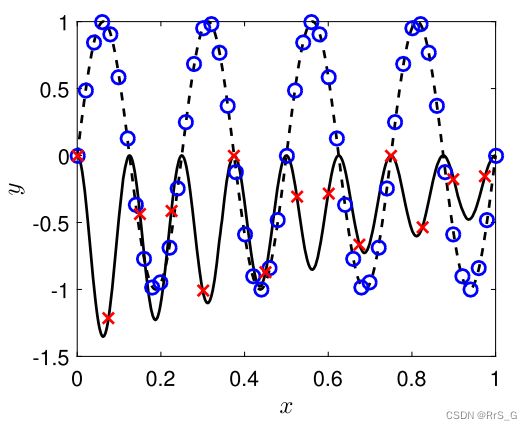
与之前一样,仅利用少数高保真数据点,无法对高保真值进行准确的预测。如下图所示:
然后基于多保真度训练数据对多保真度DNN进行性能测试。 同样,从本模型的预测值与精确值在高保真水平上很好地吻合,如下图所示。
有趣的是,尽管有时候低保真数据的趋势与高保真数据相反,多保真DNN仍然可以对高保真值进行准确的预测。
此外,如下图所示,学习到的低保真度和高保真度数据之间的相关性与精确的相关性非常吻合。
(x, yL, yH)平面中的红色虚线表示Eq.(5)(在确切的黑色实线之上),(yL, yH)平面中的红色虚线表示发现的高保真度和低保真度数据之间的相关性。
3.1.3. 20维函数的近似
从以下方程生成20维函数的低保真和高保真数据:
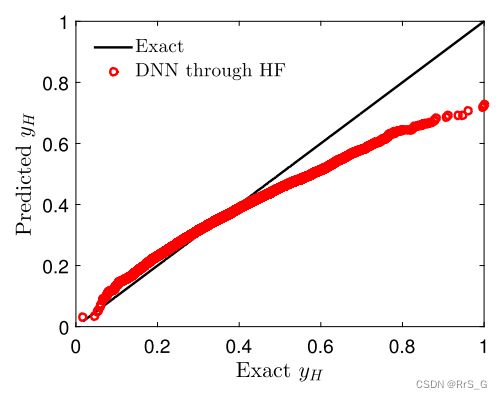
如下图所示,仅使用可用的高保真数据不能得到精确的函数逼近。
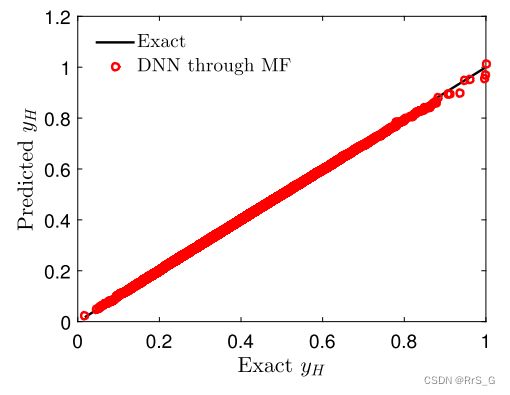
但使用多保真DNN方法可以得到如下图所示的优异结果。
3.2. 非线性反偏微分方程问题
本节将把多保真PINNs (MPINNs)应用到具有非线性的PDE反问题。
3.2.1. 学习非饱和非线性流动的水力导率
这里考虑一维(1D)柱中稳定的不饱和流动,其含水量变化,可以用下面的方程来描述
考虑两种边界条件,(1)入口流量恒定,出口压头恒定,![]() (case 1). (2)入口和出口均保持恒压水头,
(case 1). (2)入口和出口均保持恒压水头,![]() (case 2).
(case 2).
![]() 是柱子的长度,h是压头,h0、h1分别为进口和出口的压头,q表示通量,q0是入口的通量,是一个常数。另外,K(h)为压力相关的水力导率,表达式为
是柱子的长度,h是压头,h0、h1分别为进口和出口的压头,q表示通量,q0是入口的通量,是一个常数。另外,K(h)为压力相关的水力导率,表达式为
![]() 是饱和导水率,
是饱和导水率,![]() 是有效饱和度,是h的函数。
是有效饱和度,是h的函数。
αo与进气吸力逆相关,m表示孔径分布的测度。目标得到K(h)的分布,但是这两个参数不能直接测量得到,但是与α0和m相比,可以更容易地测量压头h。因此假设h的部分测量是可用的。目标是根据h的观测估计α0和m。然后,可以根据公式计算K(h)的分布。
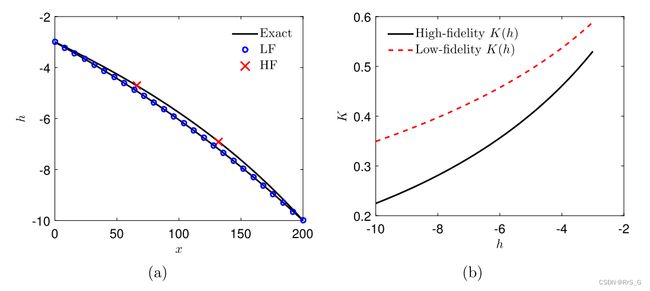
为了获得训练数据,利用Matlab中的bvp4c(均匀格点,δx = 1/15cm)进行了两种类型的数值模拟,以生成低保真和高保真数据。
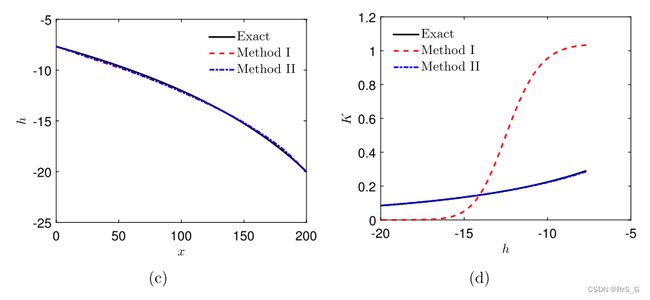
1、首先考虑入口流量恒定的流量。将方程编码到MPINNs中的最后一个神经网络中。如下图所示,水力传导率的预测与精确解不同。
根据Darcy’s定律,可以将式(22)改写为
考虑入口q = qo是一个常数,可以得到如下方程
然后在MPINN中使用该式代替Eq.(22),结果有了很大的改善,结果如下图。
然后对于MPINN和PINN,学习到的压头和水力传导率如下图所示:
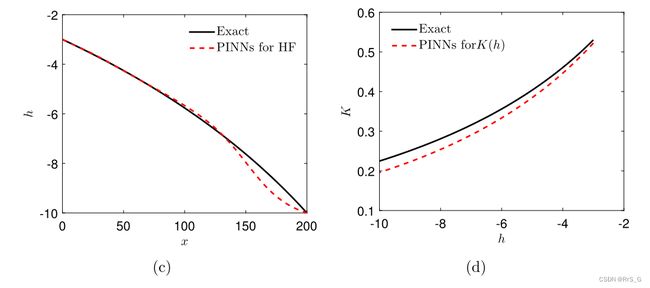
(a)、只使用高保真数据的PINN训练预测h。(b)、仅使用高保真数据的PINN训练预测K。
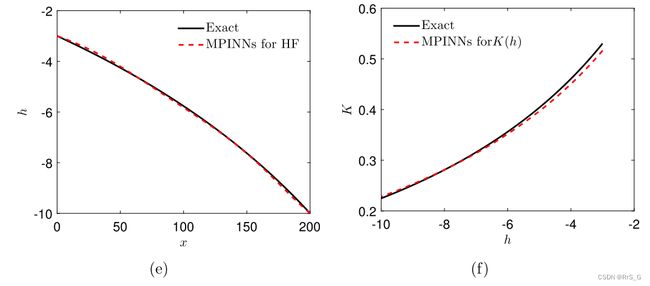
(c)、使用具有多保真度数据的MPINN预测h。(d)、使用具有多保真度数据的MPINN预测K。
2、对于Case 2,设置入口和出口的压头为h0 =−3cm, h1 =−10cm。还假设入口的通量是已知的,因此在MPINN中也可以使用Eq.(26)来代替Eq.(22)。训练数据如图9(a)所示。这里的神经网络的大小与案例I中使用的保持一致。我们观察到,本案例的结果(图9(c)-9(f))与案例I中的结果非常相似。
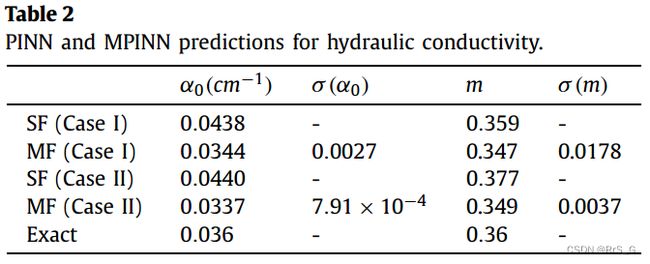
最后,α0的平均值以及不同初始猜测的m值如表2所示,这表明与仅基于高保真度的估计相比,MPINN可以显著提高预测精度(SF在表2中)。
四、前景
本文提出的新MPINNs可以用很少的高保真数据对未知参数甚至函数进行高精度识别,这在降低采集高保真数据的高实验成本方面很有前景。