Surf算法

   2006年提出，对特征点进行提取和描述的实时性算法，对尺度缩放、旋转、亮度变化都有很好的适应性和稳定性。主要步骤有4个：

1）图像灰度化

2）特征点提取：①构造尺度空间；②求出海塞矩阵行列式图像；③特征点过滤

3）特征点描述：①特征点主方向计算；②生成特征描述

4）特征点匹配

1.1特征点提取

    ①构造尺度空间：在构建Hessian矩阵前先对图像进行高斯滤波，用不同的σ对图像进行高斯滤波（加权平均），得到不同尺度的图像即不同模糊程度的图像。

    Surf算法采用不同的高斯模板大小得到不同尺度的图像，一共分为四组，每组四个不同尺度的图像。

    ②求出海塞矩阵行列式图像：由多元函数的二阶偏导数构成的方阵，对于一个图像f(x,y)，其海塞矩阵为：

   

经过高斯滤波的海赛矩阵公式如下：

海塞矩阵的行列式值为：

DetH=Lxx*Lyy-0.9*Lxy2

    高斯平滑+求3个二阶导数，引入积分图像的概念：对于一幅灰度的图像，积分图像中的任意一点(x,y)的值是指从图像的左上角到这个点所构成的矩形区域内所有点的灰度值和。

    两幅图是9*9盒式滤波器分别在图像上垂直方向上二阶导数Lyy和Lxy对应的值，灰色部分的像素值为0，黑色为-2，白色为1。

    ③特征点过滤

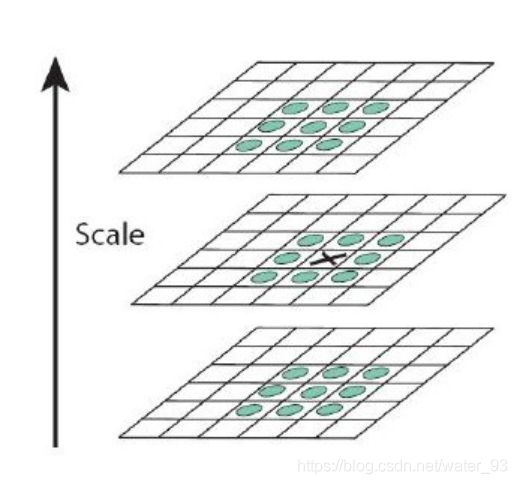
    Hessian矩阵处理过的每个像素点与其同层的8邻域点以及上一层和下一层的各9个点，即一共26个三维邻域点的大小进行比较，如果它是这26个点中的最大值或者最小值，则保留下来，当做初步确定的关键点(特征点)

2.2特征点描述

①特征点主方向计算

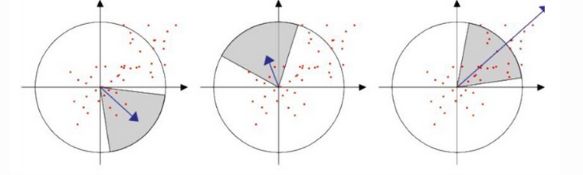
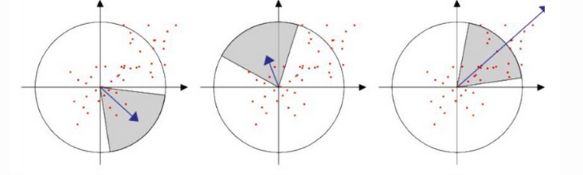
   统计特征点圆形邻域内的Harr特征，即在特征点的圆形邻域内，统计60度扇形内所有点的水平、垂直Harr小波特征总和，然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内Harr小波特征值之后，最后将Harr小波特征值最大的那个扇形方向作为该特征点的主方向。该过程示意图如下：

 

 

②生成特征描述（64维harr特征向量）

    对每个特征点周围的4*4邻域，计算每个子区域的4个Harr小波特征值，这4个值作为每个子区域的特征向量，所以一共有4*4*4=64维向量作为Surf特征描述子。

一、前言

1.图像一阶导数

    在微积分中，一维函数的一阶微分的基本定义是这样的：

 

dfdx=limε→0fx+ε-f(x)ε

    因为图像是一个离散的二维函数，ε不能无限小，我们的图像是按照像素来离散的，最小的ε就是1像素。因此，上面的图像微分又变成了如下的形式（ε=1）：

∂f(x,y)∂x=fx+1,y-fx,y= fx,y- fx-1,y= gx

∂f(x,y)∂y=fx,y+1-fx,y= fx,y- fx,y-1=gy

    x方向和y方向结合的梯度Mx,y如下：

Mx,y=gx+gy

 

 

2.图像二阶导数

∂2f∂x2=∂f∂x'= f'x+1-f'x

              = fx+1-fx-fx- fx-1

        = fx+1+fx-1-2 fx

 

二、Surf算法

    2006年提出，对特征点进行提取和描述的实时性算法，对尺度缩放、旋转、亮度变化都有很好的适应性和稳定性。主要步骤有4个：

1）图像灰度化

2）特征点提取：①构造尺度空间；②求出海塞矩阵行列式图像；③特征点过滤

3）特征点描述：①特征点主方向计算；②生成特征描述

4）特征点匹配

2.1特征点提取

    ①构造尺度空间：在构建Hessian矩阵前先对图像进行高斯滤波，用不同的σ对图像进行高斯滤波（加权平均），得到不同尺度的图像即不同模糊程度的图像。

    Surf算法采用不同的高斯模板大小得到不同尺度的图像，一共分为四组，每组四个不同尺度的图像。

    ②求出海塞矩阵行列式图像：由多元函数的二阶偏导数构成的方阵，对于一个图像f(x,y)，其海塞矩阵为：

Hx,y=∂2f∂x2∂2f∂x∂y∂2f∂x∂y∂2f∂y2

   

经过高斯滤波的海赛矩阵公式如下：

Hx,σ=Lxxx,σLxyx,σLxyx,σLyyx,σ

海塞矩阵的行列式值为：

DetH=Lxx*Lyy-0.9*Lxy2

    高斯平滑+求3个二阶导数，引入积分图像的概念：对于一幅灰度的图像，积分图像中的任意一点(x,y)的值是指从图像的左上角到这个点所构成的矩形区域内所有点的灰度值和。

    两幅图是9*9盒式滤波器分别在图像上垂直方向上二阶导数Lyy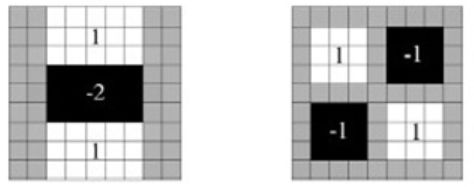和Lxy对应的值，灰色部分的像素值为0，黑色为-2，白色为1。

    ③特征点过滤

    Hessian矩阵处理过的每个像素点与其同层的8邻域点以及上一层和下一层的各9个点，即一共26个三维邻域点的大小进行比较，如果它是这26个点中的最大值或者最小值，则保留下来，当做初步确定的关键点(特征点)

2.2特征点描述

①特征点主方向计算

   统计特征点圆形邻域内的Harr特征，即在特征点的圆形邻域内，统计60度扇形内所有点的水平、垂直Harr小波特征总和，然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内Harr小波特征值之后，最后将Harr小波特征值最大的那个扇形方向作为该特征点的主方向。该过程示意图如下：

 

 

②生成特征描述（64维harr特征向量）

    对每个特征点周围的4*4邻域，计算每个子区域的4个Harr小波特征值，这4个值作为每个子区域的特征向量，所以一共有4*4*4=64维向量作为Surf特征描述子。