手把手教你理解SURF算法的全部过程
首先介绍下SURF算法的流程,具体原理后面再介绍
一.对原图像进行积分图像处理
我们知道原始图像h(x,y)是二维空间的离散点,值的大小是每个像素点的灰度值。转化为积分图像的方法g(x)的方法是,g(x,y) 对应 以f(1,1)和以f(x,y)为对角线的矩阵内的所有像素点的累加和,很简单,例如要求g(2,3) ,就是f(1,1)+f(1,2)+f(1,3)+f(2,1)+f(2,2)+f(2,3).这样子。
这样我们就得到了一个积分图像g(x,y)
至于这样做有什么用后面会介绍
二. 盒子滤波器
第二行的三个图便是我们要用的三个盒子模型滤波器,分别是Dxx,Dyy,Dxy,就是对x的二阶偏导,对y的二阶偏导,还有对xy的混合偏导。
图中边缘的灰色部分的值为0,白色是1,黑色的是-2
积分图像和盒子滤波器一起使用就相当于原图像经过高斯滤波再进行Hessian矩阵变换
那么为什么盒式滤波器可以提高运算速度呢,这就涉及到积分图的使用。盒式滤波器对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题,这正是积分图的强项,只需要简单几次查找积分图就可以完成。
三.构建尺度空间
不同于SIFT的对原始图像进行降采样以构建金字塔,SURF则保持原始图像尺寸不变,不断扩大滤波器的尺寸
如前所述,我们使用9×9的模板对图像进行滤波,其结果作为最初始的尺度空间层(此时,尺度值为s=1.2,近似σ=1.2的高斯微分),后续的层将通过逐步放大滤波模板尺寸,以及放大后的模板不断与图像进行滤波得到。由于采用盒子滤波和积分图像,滤波过程并不随着滤波模板尺寸的增加而使运算工作量增加。
与SIFT算法类似,我们需要将尺度空间划分为若干组(Octaves)。一个组代表了逐步放大的滤波模板对同一输入图像进行滤波的一系列响应图。每个组又由若干固定的层组成。由于积分图像离散化的原因,两个层之间的最小尺度变化量是由高斯二阶微分滤波器在微分方向上对正负斑点响应长度L0决定的,它是盒子滤波器模板尺寸的1/3。对于9×9的模板,它的L0=3。下一层的响应长度至少应该在L0的基础上增加2个像素,以保证一边一个像素,即L0=5。这样模板的尺寸就为15×15。以此类推,我们可以得到一个尺寸增大模板序列,它们的尺寸分别为:9×9,15×15,21×21,27×279×9,15×15,21×21,27×27,黑色、白色区域的长度增加偶数个像素,以保证一个中心像素的存在。
放一张图说明每组,包括组内各层的滤波器尺寸大小
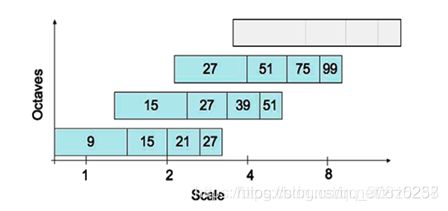
横的每一行表示每组内部的四个滤波器的尺寸大小,细心的话会发现相邻组之间的滤波器尺寸会有重叠,这个下节就会解释。

每次我们要对一个图像用三个不同滤波器处理(如上图所示),之后再进行处理后得到Hessiam行列式图像
具体的处理方式是 Dxx * Dyy -(0.9 * Dxy)^2
这里的0.9就是为了弥补我们之前用盒子滤波器+积分图像代替高斯滤波所带来的误差
0.9的由来见下图

这样经过滤波之后我们就会得到一系列经过滤波处理后的图像
四.兴趣点的定位(包含特征点和将要被筛除的点)
想象一下,我们现在已经得到了很多层的Hessiam行列式图像,一共有很多组,每组内部有四层,
这里我们只对每组组内中间的两层内的所有点进行极值检测,最顶的一层因为缺少上一层而最底部一层因为缺少下层而不进行极值检测(这就解释了为什么相邻的组之间的各滤波器尺寸会有重叠部分)

极值检测就是中心点与自己周围的26个点进行比较,检测其是否为最大值点或者是最小值点,除此之外,还要将其与我们设置的极值阈值进行比较,进行筛选,只留下一些强特征点,到此为止,我们的特征点就寻找完毕了
五.特征点的特征矢量的生成(为了满足旋转不变性)
我们需要为每个特征点分配一个主方向,这就是主方向的选取问题,以特征点为圆心,以6*s(s=1.2∗L/9为特征点的尺度)为半径,对图像进行Haar小波响应运算(这里的图像指的是原始图像f(x,y)),不过进行小波运算的时候还会用到积分图像。
用其对圆形领域进行处理后,就得到了该领域内每个点对应的x,y方向的响应,然后用以兴趣点为中心的高斯函数(σ =2s)对这些响应进行加权。
为了求取主方向值,需要设计一个以特征点为中心,张角为60度的扇形滑动窗口,统计这个扇形区域内的haar小波特征总和。以步长为0.2弧度左右,旋转这个滑动窗口,再统计小波特征总和。小波特征总和最大的方向为主方向。特征总和的求法是对图像Harr小波响应值dx、dy进行累加,得到一个矢量
主方向为最大Harr响应累加值所对应的方向,也就是最长矢量所对应的方向
至此,每个特征点的主方向确认完毕
六.特征点特征矢量的生成
SURF中,我们在关键点周围选取一个正方形框,方向为关键点的主方向,边长为20S。将其划分为16个区域(边长为5S),每个区域统计25个像素的水平方向和垂直方向的Haar小波特性(均相对于正方形框的主方向确定的)
生成特征点描述子,需要计算图像的Haar小波响应。在一个矩形区域来计算Haar小波响应。以特征点为中心,沿上一节讨论得到的主方向,沿主方向将20s×20s的图像划分为4×4个子块,每个子块利用尺寸2s的Harr模板进行响应值计算,然后对响应值进行统计∑dx、∑|dx|、∑dy、∑|dy|形成特征矢量。
这样,每个特征点可以用一个1 * 64 的向量来表示(444 = 64)
随后对两幅图像的特征向量进行匹配
七.补充
最近因为要写毕业论文,论文的方向就是图像配准相关,为此花了近一个月的时间学习了SIFT和SURF算法。
记录下自己收获最大的知识点。
首先是构建金字塔的目的
两个待匹配图像中的两个物体的尺寸因为拍摄距离等原因可能在图像上面是不同的,例如同一个水杯,站在近处拍摄,得到A图上面的水杯尺寸大小是20×80,站在远处拍,B图上拍出来的尺寸是10×40,但是它们确实是同一个水杯啊,但是若是没有金字塔模型,两个图片中的水杯部分的特征点的特征向量很有可能匹配不上(具体原因我也说不清楚),但是有了金字塔之后就不一样了,拿SIFT算法来说,我们要对原始图像不断进行降采样处理来得到金字塔,A图经过一次降采样之后,图片整体尺寸变为原来的一般,里面的水杯也就自然变成了10×40的大小,这样这一降采样之后的图像就可以刚好和B图的原始图像匹配上,当然也不是说必须要尺寸完全一样才可以,但是我们总能找到尺寸最相似的一组
至于SURF算法中不断扩张盒子滤波器的大小,我想这可以起到相似的作用
另一个是主方向的确立
还拿上面的例子,一个杯子可以横着拍,也可以竖着拍,当然也可以斜着拍,如果不进行方向归一化,很可能因为特征向量的内部错位而导致匹配失败,这就需要统一一个标准方向。这就为SIFT算法和SURF算法实现旋转不变性提供了可能
