python 强化学习Q-Learning 算法简单应用

 Algorithm 3. The SARSA algorithm.

1:Let be a set of states, and (), ∈ , be a set of actions available in the state .

2:Initialize(,),∈,isnotterminal,∈()arbitrarily

3:Initialize and

4:for each game do

5:        Initialize a nonterminal state 0 at random

6:        Select 0 under the policy 0(|0)

7:        ←0

8:        for each step of the game until a stopping criterion is reached or until

is a nonterminal state, do

9:                Take action , find +1, transition to +1

10:               if +1 is a terminal state, then

11:                       (, ) ← (, ) + (+1 − (, ))

12:               else

13:                       Select +1 under the policy +1(|+1)

14:                       (, ) ← (, ) + (+1 + (+1, +1) − (, ))

15:                end if

16:                 ← (+1)

17:        end if

18:end for

#程序包含以下内容
#使用SARSA方法，进行40000场冰湖游戏
#使用训练完的模型进行游戏
#画出智能体的移动路径
epsilon = 0.1 # Epsilon parameter which is used in epsilon-greedy strategy
gamma = 0.9 # Discount coefficient gamma
random_seed = 2 #Random seed
time_delay = 1 # Time delay when rendering the game process after training (seconds)
lr_rate = 0.9 #Learning rate alpha
import time

# %% md


# %%SARSA

import gym
import numpy as np
import time
from IPython.display import clear_output


def generate_random_map(size, p, sd):
    """Generates a random valid map (one that has a path from start to goal)
    :param size: size of each side of the grid
    :param p: probability that a tile is frozen
    """
    valid = False
    np.random.seed(sd)

    # DFS to check that it's a valid path.
    def is_valid(res):
        frontier, discovered = [], set()
        frontier.append((0, 0))
        while frontier:
            r, c = frontier.pop()
            if not (r, c) in discovered:
                discovered.add((r, c))
                directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]
                for x, y in directions:
                    r_new = r + x
                    c_new = c + y
                    if r_new < 0 or r_new >= size or c_new < 0 or c_new >= size:
                        continue
                    if res[r_new][c_new] == 'G':
                        return True
                    if (res[r_new][c_new] not in '#H'):
                        frontier.append((r_new, c_new))
        return False

    while not valid:
        p = min(1, p)
        res = np.random.choice(['F', 'H'], (size, size), p=[p, 1 - p])
        res[0][0] = 'S'
        res[-1][-1] = 'G'
        valid = is_valid(res)
    return ["".join(x) for x in res]


# Map generation
random_map = generate_random_map(size=6, p=0.8, sd=random_seed)  # Create our map
env = gym.make("FrozenLake-v0", desc=random_map, is_slippery=False)  # Initialize environment
print("Your map")
env.render()  # Render the map


def choose_action(state):
    action = 0
    if np.random.uniform(0, 1) < epsilon:
        action = np.random.randint(0, env.action_space.n)  # ***
    else:
        action = np.random.choice(np.array(np.argwhere(Q[state, :] == np.amax(Q[state, :])).flatten().tolist()))
    return action


def learn(state, state2, reward, action, action2, done):
    if done is True:
        Q[state, action] = Q[state, action] + lr_rate * (reward - Q[state, action])
    else:
        Q[state, action] = Q[state, action] + lr_rate * (reward + gamma *Q[state2, action2] - Q[state, action])
    # Q[state, action] = #Your code here



from tqdm import tqdm

# Inititalization
np.random.seed(random_seed)
total_games = 40000
max_steps = 100
Q = np.zeros((env.observation_space.n, env.action_space.n))
# Main cycle
game1 = [0] * total_games
for game in tqdm(range(total_games)):
    state = env.reset()
    t = 0
    action = choose_action(state)
    while t < max_steps:
        # env.render()
        t += 1

        state2, reward, done, info = env.step(action)
        if t == max_steps:
            done = True
        action2 = choose_action(state2)
        learn(state, state2, reward, action, action2, done)

        state = state2

        action = action2
        if done:
            if reward == 1:
                game1[game] = 1
            break


def get_fg_and_v(game):
    v = 0
    fg = 0
    i = 0
    l = []
    for g in game:
        if g == 1:
            v = v + 1
            if len(l) == 0:
                l.append(i)
            else:
                if len(l) < 5:
                    if l[-1] - i == -1:
                        l.append(i)
                    else:
                        l = [i]
                    if len(l) == 5 and fg == 0:
                        fg = i + 1

        i = i + 1
    return fg, v


fg, v = get_fg_and_v(game1)

# 1
print("The number of victories in a series of 10,000 games: ", v)  # Your code here
# 2
print("Five wins in a row were first won in the game ", fg)  # Your code here

import time


# Greedy action selection
def choose_action_one_game(state):
    action = np.random.choice(np.array(np.argwhere(Q[state, :] == np.amax(Q[state, :])).flatten().tolist()))
    return action


states = []  # Array to save agent states during the game
t = 0
state = env.reset()
wn = 0
while (t < 100):
    # env.render()
    time.sleep(time_delay)
    clear_output(wait=True)
    action = choose_action_one_game(state)
    state2, reward, done, info = env.step(action)
    states.append(state)
    state = state2
    t += 1
    if done and reward == 1:
        wn = 1
    if done:
        break
if wn == 1:
    print("!!!WIN!!!")

import matplotlib.pyplot as plt


def make_maze_pic(maze):
    maze_pic = []
    for i in range(len(maze)):
        row = []
        for j in range(len(maze[i])):
            if maze[i][j] == 'S':
                row.append(0)
            if maze[i][j] == 'F':
                row.append(0)
            if maze[i][j] == 'H':
                row.append(1)
            if maze[i][j] == 'G':
                row.append(0)
        maze_pic.append(row)
    maze_pic = np.array(maze_pic)
    return maze_pic


# Make maze fit to plot
maze_pic = make_maze_pic(random_map)
nrows, ncols = maze_pic.shape

# Arrays of picture elements
rw = np.remainder(states, nrows)
cl = np.floor_divide(states, nrows)
if wn == 1:
    rw = np.append(rw, [nrows - 1])
    cl = np.append(cl, [ncols - 1])

# Picture plotting
fig, ax1 = plt.subplots(1, 1, tight_layout=True)
ax1.clear()
ax1.set_xticks(np.arange(0.5, nrows, step=1))
ax1.set_xticklabels([])
ax1.set_yticks(np.arange(0.5, ncols, step=1))
ax1.set_yticklabels([])
ax1.grid(True)
ax1.plot([0], [0], "gs", markersize=40)  # start is a big green square
ax1.text(0, 0.2, "Start", ha="center", va="center", color="white", fontsize=12)  # Start text
ax1.plot([nrows - 1], [ncols - 1], "rs", markersize=40)  # exit is a big red square
ax1.text(nrows - 1, ncols - 1 + 0.2, "Finish", ha="center", va="center", color="white", fontsize=12)  # Exit text
ax1.plot(rw, cl, ls='-', color='blue')  # Blue lines path
ax1.plot(rw, cl, "bo")  # Blue dots visited cells
ax1.imshow(maze_pic, cmap="binary")
fig.show()
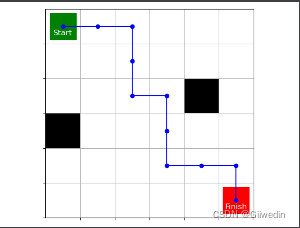
# 3

智能体的移动路径如下：

 

Algorithm 4. Q-learning algorithm

1:Let be a set of states, and (), ∈ , be a set of actions available in the state .

2:Initialize(,),∈,isnotterminal,∈()arbitrarily

3:Initialize and

4:for each game do

5:        Initialize a nonterminal state 0 at random

6:        ←0

7:        for each step of the game until a stopping criterion is reached or until

is a nonterminal state, do

8:                Select under the policy (|)

9:                Take action , find +1, transition to +1

10:               if +1 is a terminal state, then

11:                       (, ) ← (, ) + (+1 − (, ))

12:               else

13:                       (, ) ← (, ) + (+1 + max((+1, a)) − (, ))

14:                end if

15:                 ← (+1)

16:        end if

17:end for

#程序包含以下内容
#使用Q-learning方法，进行10000场冰湖游戏
#使用训练完的模型进行游戏
#画出智能体的移动路径
epsilon = 0.1 # Epsilon parameter which is used in epsilon-greedy strategy
gamma = 0.9 # Discount coefficient gamma
random_seed = 6 #Random seed
time_delay = 1 # Time delay when rendering the game process after training (seconds)
lr_rate = 0.9 #Learning rate alpha
import time

#%% md


#%%Q-Learning

import gym
import numpy as np
import time
from IPython.display import clear_output


def generate_random_map(size, p, sd):
    """Generates a random valid map (one that has a path from start to goal)
    :param size: size of each side of the grid
    :param p: probability that a tile is frozen
    """
    valid = False
    np.random.seed(sd)

    # DFS to check that it's a valid path.
    def is_valid(res):
        frontier, discovered = [], set()
        frontier.append((0,0))
        while frontier:
            r, c = frontier.pop()
            if not (r,c) in discovered:
                discovered.add((r,c))
                directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]
                for x, y in directions:
                    r_new = r + x
                    c_new = c + y
                    if r_new < 0 or r_new >= size or c_new < 0 or c_new >= size:
                        continue
                    if res[r_new][c_new] == 'G':
                        return True
                    if (res[r_new][c_new] not in '#H'):
                        frontier.append((r_new, c_new))
        return False

    while not valid:
        p = min(1, p)
        res = np.random.choice(['F', 'H'], (size, size), p=[p, 1-p])
        res[0][0] = 'S'
        res[-1][-1] = 'G'
        valid = is_valid(res)
    return ["".join(x) for x in res]

# Map generation
random_map = generate_random_map(size=6, p=0.8, sd = random_seed) #Create our map
env = gym.make("FrozenLake-v0", desc=random_map, is_slippery=False) #Initialize environment
print("Your map")
env.render() #Render the map

def choose_action(state):
    action=0
    if np.random.uniform(0, 1) < epsilon:
        action = np.random.randint(0,env.action_space.n) #***
    else:
        action = np.random.choice(np.array(np.argwhere(Q[state, :] == np.amax(Q[state, :])).flatten().tolist()))
    return action

def learn(state, state2, reward, action, done):
    if done is True:
        Q[state, action] = Q[state, action] + lr_rate*(reward - Q[state, action])
    else:
        Q[state, action] = Q[state, action] + lr_rate * (reward + gamma*np.max(Q[state2,:])-Q[state, action])
    #Q[state, action] = #Your code here


#Q-learning
from tqdm import tqdm
# Inititalization
np.random.seed(random_seed)
total_games = 10000
max_steps = 100
Q = np.zeros((env.observation_space.n, env.action_space.n))
# Main cycle
game1= [0]*total_games
for game in tqdm(range(total_games)):
    state = env.reset()
    t = 0
    while t < max_steps:
        #env.render()
        t += 1

        action = choose_action(state)

        state2, reward, done, info = env.step(action)
        if t == max_steps:
            done = True

        learn(state, state2, reward, action, done)

        state = state2

        if done:
            if reward == 1:
                game1[game]=1
            break
def get_fg_and_v(game):
    v = 0
    fg=0
    i=0
    l=[]
    for g in game:
        if g ==1:
            v=v+1
            if len(l) ==0:
                l.append(i)
            else:
                if len(l) <5:
                    if l[-1] - i == -1:
                        l.append(i)
                    else:
                        l=[i]
                    if len(l) == 5 and fg==0:
                        fg = i+1

        i=i+1
    return fg , v
fg,v=get_fg_and_v(game1)


print("The number of victories in a series of 10,000 games: ",v)#Your code here
print("Five wins in a row were first won in the game ",fg)#Your code here



import time
#Greedy action selection
def choose_action_one_game(state):
    action = np.random.choice(np.array(np.argwhere(Q[state, :] == np.amax(Q[state, :])).flatten().tolist()))
    return action

states=[]#Array to save agent states during the game
t = 0
state = env.reset()
wn = 0
while(t<100):
  #env.render()
  time.sleep(time_delay)
  clear_output(wait=True)
  action = choose_action_one_game(state)
  state2, reward, done, info = env.step(action)
  states.append(state)
  state = state2
  t += 1
  if done and reward == 1:
    wn=1
  if done:
    break
if wn == 1:
  print("!!!WIN!!!")

import matplotlib.pyplot as plt


def make_maze_pic(maze):
    maze_pic = []
    for i in range(len(maze)):
        row = []
        for j in range(len(maze[i])):
            if maze[i][j] == 'S':
                row.append(0)
            if maze[i][j] == 'F':
                row.append(0)
            if maze[i][j] == 'H':
                row.append(1)
            if maze[i][j] == 'G':
                row.append(0)
        maze_pic.append(row)
    maze_pic = np.array(maze_pic)
    return maze_pic


# Make maze fit to plot
maze_pic = make_maze_pic(random_map)
nrows, ncols = maze_pic.shape

# Arrays of picture elements
rw = np.remainder(states, nrows)
cl = np.floor_divide(states, nrows)
if wn == 1:
    rw = np.append(rw, [nrows - 1])
    cl = np.append(cl, [ncols - 1])

# Picture plotting
fig, ax1 = plt.subplots(1, 1, tight_layout=True)
ax1.clear()
ax1.set_xticks(np.arange(0.5, nrows, step=1))
ax1.set_xticklabels([])
ax1.set_yticks(np.arange(0.5, ncols, step=1))
ax1.set_yticklabels([])
ax1.grid(True)
ax1.plot([0], [0], "gs", markersize=40)  # start is a big green square
ax1.text(0, 0.2, "Start", ha="center", va="center", color="white", fontsize=12)  # Start text
ax1.plot([nrows - 1], [ncols - 1], "rs", markersize=40)  # exit is a big red square
ax1.text(nrows - 1, ncols - 1 + 0.2, "Finish", ha="center", va="center", color="white", fontsize=12)  # Exit text
ax1.plot(rw, cl, ls='-', color='blue')  # Blue lines path
ax1.plot(rw, cl, "bo")  # Blue dots visited cells
ax1.imshow(maze_pic, cmap="binary")
fig.show()

智能体的移动路径如下：