Logistic回归算法

一、前言

Logistic回归虽然名字上是叫回归，但其实它是一种分类算法。Logistic回归也在一些文献中也称为logit回归、最大熵分类(MaxEnt)或对数线性分类器。

“回归”的意思就是要找到最佳拟合参数，其中涉及的数学原理和步骤如下：

1. 需要一个合适的分类函数来实现分类。可以使用单位阶跃函数或者Sigmoid函数。
2. 用 代价函数 来表示 预测值h(x) 与 实际值y 的偏差 (h−y)。要使得回归最佳拟合，那么偏差要尽可能小（偏差求和或取均值）。
3. 记J(w,b)表示回归系数取w时的偏差，那么求最佳回归参数w,b就转换成了求J(w,b)的最小值。可以使用梯度下降法求回归参数w,b。

所以，接下来就围绕这几个步骤进行展开。

二、分类函数

2.1 二项Logistic回归模型

（1）假设要实现二分类，那么可以找一个函数，根据不同的特征变量，输出0和1，并且只输出0和1，这种函数在某个点直接从0跳跃到1，如图：

但是这种函数处理起来，稍微有点麻烦。

（2）我们选择另外一个连续可导的函数，也就是Sigmoid函数,函数的公式如下：

$y=h(z)=\frac{1}{1+e^{-z}}（y就表示预测值也就是分类结果）$

这个函数的特点是，当z=0时，h(z)=0.5，而z越大，h(z)越接近1，z越小，h(z)越接近0。这个函数很像阶跃函数，当z>0，就可以将数据分入1类；当z < 0，就可以将数据分入0类。函数图如下：

确定了分类函数，接下来，我们将Sigmoid函数的输入记为z，那么输入特征变量为：

$z=w_0{x}_0+w_1{x}_1+...+w_n{x}_n+b=w^{T}x+b$，w是特征向量，b是一个值。

则分类函数（假设函数）：$y=h(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(w^{T}x+b)}}$

其中，向量x是特征变量，是输入数据，向量w,b是回归系数是特征。之后的事情就是如何确定最佳回归系数w(w0,w1,w2,…,wn,b)。

采用Sigmoid函数实际上就是将原始的输入x向量和某一合适的参数w向量相乘，得出的值作为sigmoid函数的输入，最终是的输出保持在0和1这两个值中的一个，从而达到分类的要求。

假设函数的计算结果就是分类属于y=1的概率p，分类属于0的概率是1-p。如果p>0.5就分为1类，否则分为0类。

2.2 多项Logistic回归

上面的二项Logistic回归适用于二分类，对于多分类问题，假设离散型随机变量Y的取值集合是{1,2,…,K}，那么Logistic回归模型是：

$$\hat{y}=\{\begin{array}{ll}& p(Y=k|x)=\frac{exp(w_k\cdot x)}{1+\sum _{k=1}^{K-1}exp(w_k\cdot x)},k=1,2,...,K-1\\ & p(Y=K|x)=\frac{1}{1+\sum _{k=1}^{K}exp(w_k\cdot x)},k=K\end{array}$$

三、损失函数和代价函数

1.损失函数（Loss function）

首先要知道损失函数是应用于单独一个训练样本的。而下面要说的代价函数则是针对整个训练集。

为了更好的进行凸优化，我们这里直接给出一个适合Logistic函数的损失函数：

$L(y,y)=-[ylogy+(1-y)log(1-y)]$

来看一下这个损失函数的特点：

• 当y=1时，$ylogy$ 这个部分的值是$logy，y表示预测分类$，$(1-y)log(1-y)$ 这个部分的值是0。所以最终的损失函数是：$L(y,y)=-logy$，而我们要求损失函数越小越好，所以也就是要求 $-(logy)$ 越小越好，也就是要求 $y$ 越大越好。而 $y$和y一样，范围都是在0-1之间，所以 $y$ 越接近于1（y=1），损失函数越小。
• 当y=0时，$ylogy$ 这个部分的值是$0，y表示预测分类$，$(1-y)log(1-y)$ 这个部分的值是 $log(1-y)$。所以最终的损失函数是：$L(y,y)=-(1-y)log(1-y)$，而我们要求损失函数越小越好，所以也就是要求 $-[(1-y)log(1-y)]$ 越小越好，也就是要求 $y$ 越小越好，所以 $y$ 越接近于0（y=0），损失函数越小。

2.代价函数（Cost function）或者叫 成本函数。

根据上面的损失函数可以得到整个训练集的代价函数：

$J(w,b)=\frac{1}{n}{\sum }_{i=1}^{n}L(y^i,y^i)=-\frac{1}{n}{\sum }_{i=1}^n[y^{i}log{y}^i+(1-y^i)log(1-y^i)]$

由于损失函数越小，预测效果越好。所以代价函数也是越小越好。由于代价函数是一个凸函数，可以采用梯度下降法求到使得代价函数最小的时候的参数值(w,b)。

四、梯度上升/梯度下降

要使得代价函数越小越好就是要 $\frac{1}{n}{\sum }_{i=1}^n[y^{i}log{y}^i+(1-y^i)log(1-y^i)]$ 越大越好。为求最大值，这里采用梯度上升的方法。

1. 损失函数的梯度：

首先还是要明确，损失函数是针对单独一个训练样本的。

由于 $L(y,y)=-[ylogy+(1-y)log(1-y)]$ ，所以损失函数 $L(y,y)$ 对 $y$ 求导可得：

$$\begin{array}{ll}dy=\frac{dL(y,y)}{dy}& =-\frac{y}{y}+\frac{1-y}{1-y}\end{array}$$

而 $y=h(z)=\frac{1}{1+e^{-z}}$，再利用链式求导法则，损失函数 $L(y,y)$ 对 $z$ 求导可得：

$$\begin{array}{ll}dz=\frac{dL(y,y)}{dz}& =\frac{dL}{dy}\cdot \frac{dy}{dz}\\ & =(-\frac{y}{y}+\frac{1-y}{1-y})\cdot [y(1-y)]\\ & =y-y\end{array}$$

amazing…

接着再求 $d{w}_j$，由于 $z=w^{T}x+b$ ,利用链式法则可得：

$$\begin{array}{ll}d{w}_1& =\frac{\partial L}{\partial w_1}\\ & =\frac{dL}{dz}\cdot \frac{dz}{d{w}_1}\\ & =x_1\cdot dz\\ & =x_1\cdot (y-y)\end{array}$$

同理 $d{w}_2=x_2(y-y)...d{w}_n=x_n(y-y)$。

最后求db: $db=\frac{dL}{dz}\cdot \frac{dz}{db}=dz=y-y$

在训练过程中我们要我们要不断更新参数w和b以使得损失函数最小，也就是梯度更新，梯度更新的逻辑是：

• $w_j:=w_j-\alpha \cdot d{w}_j$
• $b:=b-\alpha \cdot db$
• $\alpha$ 在这里是学习速率

2. 代价函数的梯度

上面已经得出了单个训练样本的梯度更新法，接着就看在整个训练集上如何使用梯度更新法。

由于 $y=\frac{1}{1+e^{-(w^{T}x+b)}}$，所以 $d{w}_1^{(i)},d{w}_2^{(i)},...,d{w}_n^{(i)},d_b^{(i)}$ 分别表示第i个单个样本中对参数w向量中第j个分量$w_j$的导数以及对偏置b的导数。

令 $J(w,b)=\frac{1}{n}{\sum }_{i=1}^n[y^{i}log{y}^i+(1-y^i)log(1-y^i)]$,则在整个训练集上,J(w,b)对 $w_j$的偏导数是：

$$\frac{\partial J(w,b)}{\partial w_j}=\frac{1}{n}\sum _{i=1}^n\frac{\partial L(y^{(i)},y)}{\partial w_j}$$

由于对每个$w_j$都要进行梯度更新，所以我们先得到下面的伪代码：

$$\begin{array}{ll}& J=0;\\ & d_{w_1}=0,d_{w_2}=0,...d_{w_m}=0;\\ & d_b=0;\\ & fori=1ton://n个样本\\ & z^{(i)}=w^{T}x(i)+b;\\ & y^i=sigmoid(z^i);\\ & J+=-[y^{i}log{y}^{(i)}+(1-i^i)log(1-y^i)];\\ & d{z}^{(i)}=y^{(i)}-y^i;\\ & forj=1tom://m个参数\\ & d{w}_j+=x_{j}d{z}^{(i)};\\ & db+=d{z}^{(i)};\\ & J/=n;\\ & d_{w_1}/=n,d_{w_2}/=n,...d_{w_m}/=n;\\ & db/=n;\end{array}$$

注意这里$d{w}_j$没有上标，也训练集中的每个样本进行梯度运算的时候都是使用的一个全局的参数w。

在实际操作中，不建议使用for循环，可以进行向量化，使得运算更为迅速。

五、实现

1. 数据准备

先下载附件中的LRTestSet.txt，数据格式如下：

-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
......

数据没有实际意义。第一列是参数x1,第二列是参数x2，第三列是分类标签（0/1）。

假设Sigmoid函数的输入记为 z ，那么 $z=w_0+w_1{x}_1+w_2{x}_2$ ，其实$w_0$就是上面的参数b。为了方便将z表示成向量相乘的形式 $z=w^{T}x$，可以添加一个值为1的变量$x_0$，于是前面的z就变形为： $z=w_0{x}_0+w_1{x}_1+w_2{x}_2$ 。下面代码中加载数据时手动插入一列1。

# -*- coding: UTF-8 -*-
import re
import numpy as np
import random
import matplotlib.pyplot as plt
"""
从 testSet.txt 中加载数据
"""
def loadDataSet():
    dataMat = []                                                        #创建数据列表
    labelMat = []                                                       #创建标签列表
    fr = open('testSet.txt')                                            #打开文件   
    for line in fr.readlines():                                         #逐行读取
        lineArr = line.strip().split()                                  #去回车，放入列表
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])          #添加数据(x,y)
        labelMat.append(int(lineArr[2]))                                #添加标签(分类结果)
    fr.close()                                                          #关闭文件
    return dataMat, labelMat                                            #返回

"""
绘制数据点图
"""
def plotDataSet():
    dataMat, labelMat = loadDataSet()                                   #加载数据集
    dataArr = np.array(dataMat)                                         #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                  #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)                                           #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5,label='1') #绘制1样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5,label='0')             #绘制0样本
    plt.legend()
    plt.title('DataSet')                                                #绘制title
    plt.xlabel('x1'); plt.ylabel('x2')                                  #绘制label
    plt.show()                                                          #显示

if __name__ == '__main__':
    plotDataSet()

绘制结果：

$z=w^{T}x$ 这个方程未知的参数为 $w_0,w_1,w_2$ ，也就是我们需要求的回归系数(最优参数)。

2. 训练Logistic回归算法

回顾一下上面得出的梯度更新公式：$w_j:=w_j-\alpha \cdot d{w}_j$，再对照伪代码，转化成python代码：

def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)                                       #变量转换成numpy的mat
    labelMat = np.mat(classLabels).transpose()                           #标签转换成numpy的mat,并进行转置
    m, n = np.shape(dataMatrix)                                          #返回dataMatrix的大小。m为行数,n为列数。
    alpha = 0.001                                                        #移动步长,也就是学习速率,控制更新的幅度。
    maxCycles = 500                                                      #最大迭代次数
    weights = np.ones((n,1))                                             #weights就是要求的特征系数w，全部初始化为1
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)                                #梯度上升矢量化公式
        dY = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * dY          #对w执行梯度更新
    return weights.getA()                                                #将矩阵转换为数组，返回权重数组

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()           
    print(gradAscent(dataMat, labelMat))

运行结果：

[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]

也就是$w_0=4.12414349,w_1=0.48007329,w_2=-0.6168482$

由于决策边界 $w^{T}x=0$，可得 $w_0+w_1{x}_1+w_2{x}_2=0=>x_2=(-w_0-w_1{x}_1)/w_2$ 。顺便根据得出的特征值绘制一下预测函数的图像：

def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()                                   #加载数据集
    dataArr = np.array(dataMat)                                         #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                  #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)                                           #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)            #绘制负样本
    x1 = np.arange(-3.0, 3.0, 0.1)
    x2 = (-weights[0] - weights[1] * x1) / weights[2]                   #w0+w1x1+w2x2=0 => x2=(-w0-w1x1)/w2
    ax.plot(x1, x2)
    plt.title('BestFit')                                                #绘制title
    plt.xlabel('x1'); plt.ylabel('x2')                                  #绘制label
    plt.show()       

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()           
    weights = gradAscent(dataMat, labelMat)
    plotBestFit(weights)

如图：

六、改进:随机梯度上升法

1. 随机梯度算法

上述算法，要进行maxCycles次循环，每次循环中矩阵会有mn次乘法计算，每次更新回归系数(最优参数)的时候，使用六所有的样本数据,所以时间复杂度（开销）是maxCyclesm*n，当数据量较大时，时间复杂度就会很大。因此，可以是用随机梯度上升法来进行算法改进，一次只用一个样本点去更新回归系数(最优参数)，这样就可以有效减少计算量了，这种方法就叫做随机梯度上升算法。

随机梯度上升法的思想是，每次只使用一个数据样本点来更新回归系数。这样就大大减小计算开销。

代码如下：

"""
改进后的随机梯度下降法
"""
def stocGradAscentBetter(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix)                                                  #返回dataMatrix的大小。m为行数,n为列数。
    weights = np.ones(n)                                                        #参数初始化
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01                                            #降低alpha的大小，每次减小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))                   #随机选取样本
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                     #选择随机选取的一个样本，计算h
            error = classLabels[randIndex] - h                                  #计算误差
            weights = weights + alpha * error * np.array(dataMatrix[randIndex]) #更新回归系数,注意这里要转换为numpy.array才能正确运行
            del(dataIndex[randIndex])                                           #删除已经使用的样本
    return weights

def plotBestFit(weights1,weights2):
    dataMat, labelMat = loadDataSet()                                   #加载数据集
    dataArr = np.array(dataMat)                                         #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                  #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    plt.title('BestFit')  
    plt.xlabel('x1'); plt.ylabel('x2')                                  #绘制label

    ax = fig.add_subplot(111)                                           #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)            #绘制负样本

    x1 = np.arange(-3.0, 3.0, 0.1)

    x2 = (-weights1[0] - weights1[1] * x1) / weights1[2]
    ax.plot(x1, x2,label='GradAscent')

    x22 = (-weights2[0] - weights2[1] * x1) / weights2[2]
    ax.plot(x1, x22,label='StocGradAscent')
    plt.legend()

    plt.show()

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()
    start1 = time.time()
    weights = gradAscent(dataMat, labelMat)
    start2 = time.time()
    weightsBetter = stocGradAscentBetter(dataMat, labelMat)
    plotBestFit(weights,weightsBetter)

改进后的效果和原先的差不多：

• 该算法第一个改进之处在于，alpha在每次迭代的时候都会调整 : alpha = 4/(1.0+j+i)+0.01，并且，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为这里还存在一个常数项。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果需要处理的问题是动态变化的，那么可以适当加大上述常数项，来确保新的值获得更大的回归系数。另一点值得注意的是，在降低alpha的函数中，alpha每次减少1/(j+i)，其中j是迭代次数，i是样本点的下标。
• 第二个改进的地方在于更新回归系数(最优参数)时，只使用一个样本点，并且选择的样本点是随机的，每次迭代不使用已经用过的样本点。这样的方法，就有效地减少了计算量，并保证了回归效果。

2. 回归系数与迭代次数的关系

来直观地看一下回归系数是怎么样变化地：

def gradAscent(dataMatIn, classLabels):
    weights_array = np.array([])
    dataMatrix = np.mat(dataMatIn)                                       #变量转换成numpy的mat
    labelMat = np.mat(classLabels).transpose()                           #标签转换成numpy的mat,并进行转置
    m, n = np.shape(dataMatrix)                                          #返回dataMatrix的大小。m为行数,n为列数。
    alpha = 0.001                                                        #移动步长,也就是学习速率,控制更新的幅度。
    maxCycles = 500                                                      #最大迭代次数
    weights = np.ones((n,1))                                             #weights就是要求的特征系数w，全部初始化为1
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)                                #梯度上升矢量化公式
        dY = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * dY          #对w执行梯度更新
        weights_array = np.append(weights_array,weights)
    weights_array = weights_array.reshape(maxCycles,n)    
    return weights.getA(),weights_array                                         #将矩阵转换为数组，返回权重数组

def stocGradAscentBetter(dataMatrix, classLabels, numIter=5):
    m,n = np.shape(dataMatrix)                                                  #返回dataMatrix的大小。m为行数,n为列数。
    weights = np.ones(n)                                                        #参数初始化
    weights_array = np.array([])
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01                                            #降低alpha的大小，每次减小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))                   #随机选取样本
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                     #选择随机选取的一个样本，计算h
            error = classLabels[randIndex] - h                                  #计算误差
            weights = weights + alpha * error * np.array(dataMatrix[randIndex]) #更新回归系数,注意这里要转换为numpy.array才能正确运行
            weights_array = np.append(weights_array,weights,axis=0)
            del(dataIndex[randIndex])                                           #删除已经使用的样本
    return weights,weights_array

"""
绘制回归参数和迭代次数的关系
"""
def plotWeights(weights_array0,weights_array1):
    #将fig画布分隔成1行1列,不共享x轴和y轴,fig画布的大小为(13,8)
    #当nrow=3,nclos=2时,代表fig画布被分为六个区域,axs[0][0]表示第一行第一列
    fig, axs = plt.subplots(nrows=3, ncols=2,sharex=False, sharey=False, figsize=(20,10))

    x0 = np.arange(0, len(weights_array0), 1)
    #绘制w0与迭代次数的关系
    axs[0][1].plot(x0,weights_array0[:,0])
    axs0_title_text = axs[0][0].set_title('GradAscent:weight and times')
    axs0_ylabel_text = axs[0][0].set_ylabel('w0')
    plt.setp(axs0_title_text, size=20, color='black')
    plt.setp(axs0_ylabel_text, size=20, color='black')
    #绘制w1与迭代次数的关系
    axs[1][1].plot(x0,weights_array0[:,1])
    axs0_ylabel_text = axs[1][0].set_ylabel('w1')
    plt.setp(axs0_ylabel_text, size=20,  color='black')
    #绘制w2与迭代次数的关系
    axs[2][1].plot(x0,weights_array0[:,2])
    axs0_xlabel_text = axs[2][0].set_xlabel('times')
    axs0_ylabel_text = axs[2][0].set_ylabel('w2')
    plt.setp(axs0_xlabel_text, size=20, color='black')
    plt.setp(axs0_ylabel_text, size=20, color='black')

    x1 = np.arange(0, len(weights_array1)/3, 1) #由于weights_array1是一个一行n列的数组，保存列所有的参数值，这里要处以参数的个数3
    #绘制w0与迭代次数的关系
    axs[0][0].plot(x1,weights_array1[0::3]) #[0::3]表示从位置0开始每隔3个取一位
    axs1_title_text = axs[0][1].set_title('BetterStocGradAscent:weight and times')
    axs1_ylabel_text = axs[0][1].set_ylabel('w0')
    plt.setp(axs1_title_text, size=20,  color='black')
    plt.setp(axs1_ylabel_text, size=20,  color='black')
    #绘制w1与迭代次数的关系
    axs[1][0].plot(x1,weights_array1[1::3]) #[1::3]表示从位置1开始每隔3个取一位
    axs1_ylabel_text = axs[1][1].set_ylabel('w1')
    plt.setp(axs1_ylabel_text, size=20,  color='black')
    #绘制w2与迭代次数的关系
    axs[2][0].plot(x1,weights_array1[2::3]) #[2::3]表示从未知2开始每隔3个取一位
    axs1_xlabel_text = axs[2][1].set_xlabel('times')
    axs1_ylabel_text = axs[2][1].set_ylabel('w2')
    plt.setp(axs1_xlabel_text, size=20,  color='black')
    plt.setp(axs1_ylabel_text, size=20, color='black')

    plt.show()  

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()

    start1=time.time()
    weights0,weights_array0 = gradAscent(dataMat, labelMat)
    print(time.time()-start1)

    start2=time.time()
    weights1,weights_array1 = stocGradAscentBetter(np.array(dataMat), labelMat)
    print(time.time()-start2)

    plotWeights(weights_array0, weights_array1)
    plotBestFit(weights0,weights1)

注意 gradAscent和 stocGradAscentBetter 方法中分别添加了一个全局变量 weights_array 用来保存所有迭代出来地回归参数。

下面这是将 stocGradAscentBetter方法中的numIter参数设置成5的运行结果：

运行时间：
gradAscent ： 0.0238189697265625
stocGradAscentBetter ： 0.009566068649291992

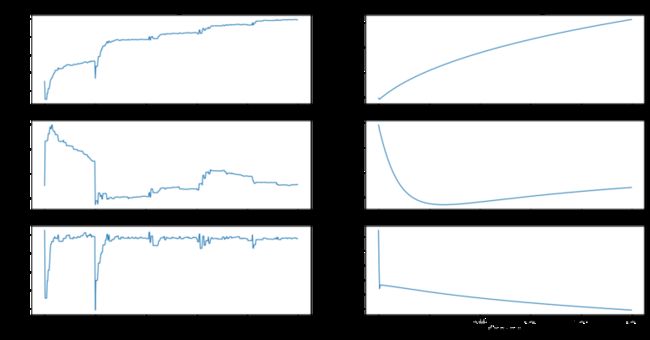
可以看到随机梯度上升算法的迭代时间比原始的梯度上升算法少很多，但是拟合效果却差别不大。并且回归参数也更快的趋于平稳。可以试着把numIter参数增大或减小，看看具体效果。

---

附：

1. LRTestSet.txt

2. code

参考：

1. 广义线性模型(Generalized Linear Models)
2. Python3《机器学习实战》学习笔记（六）：Logistic回归基础篇之梯度上升算法
3. 机器学习之Logistic回归与Python实现
4. 机器学习实战笔记5(logistic回归)
5. Logistic 回归损失函数
6. Logistic分类函数

---

THE END.