71、AdaNeRF: Adaptive Sampling for Real-time Rendering of Neural Radiance Fields

简介

官网：https://thomasneff.github.io/adanerf/

新的双网络架构，它采用正交方向，通过学习如何最好地减少所需样本点的数量，将网络分为联合训练的 sample 和 shading 网络，训练方案在每条射线上采用固定的样本位置，并在整个训练过程中逐步引入稀疏性，即使在低样本计数下也能实现高质量，在对目标样本数进行微调后，生成的紧凑神经表示可以实时呈现

贡献点：

• 一种新型的双网络架构，用于联合学习紧凑实时神经辐射场的sample 和 shading 网络，优于现有的基于sample 网络的方法。
• 额外的可调自适应采样方案，只遮挡每射线最重要的样本，在相同的平均样本计数下，进一步提高质量和效率。
• 一个实时渲染实现，依赖于紧凑的双网络表示的动态稀疏采样，目标是在性能、质量和内存之间权衡的最佳点。

实现过程

AdaNeRF采用 single-evaluation sample 网络和 multi-evaluation shading 网络，以显著减少每个视图射线所需的网络评估数量，对于每条射线，采样网络预测一个估计样本密度 $\delta$ 的向量，每个向量恰好对应一个样本位置

将原始NeRF的粗网络替换为每射线只评估一次的 sample 网络 S，最大限度地减少了生成最终图像的网络评估次数，sample 网络以射线原点 p 和射线方向 d 为输入。sample 网络的输出是一个预测向量 $\delta$，对应于沿着每条射线的样本的预测重要性。

shading 网络 T 对采样网络进行预测，对贡献最大的样本进行位置编码，输出其密度 σ 和颜色 c，通过对 sample 网络进行一次评估，可以剔除大部分贡献较小的样本，提高了管道的整体效率

End-to-end Trainable Sampling Network

将 sample 网络的预测单样本密度 ${\delta }_i$ 与 shading 网络的预测单样本密度 ${\sigma }_i$ 相乘，如此公式允许反向传播到达 sample 网络

通过沿每条射线使用固定的样本位置，并在沿每条射线离散空间时，在每个单元格的中心放置一个样本来实现。

注意，论文不要求真实深度

$\hat{C} $为估计的累积颜色，N为沿射线的样本数量，$T_i$ 为沿射线的累积透过率,$t_i$ 为相邻样本之间的距离，${\sigma }_i$ 为样本 i 的着色网络的输出密度，${\delta }_i$为采样网络预测每个采样点的密度（重要性）

引入 ${\delta }_i$ 的乘法，可以使 sample 网络通过其预测直接增加或减少样本的重要性，并从MSE颜色重建损失中接收梯度

Sparse Adaptive Sampling Network Distillation

仅仅修改射线累积并不能确保 sample 网络输出稀疏预测——它可能总是输出1个向量，导致 shading 网络在每个单元格中放置一个样本，有效地忽略了 sample 网络的预测

通过将稀疏性引入 sample 网络，将 $\delta$ 从 shading 网络密度中分离出来，这迫使网络只选择最重要的密度值

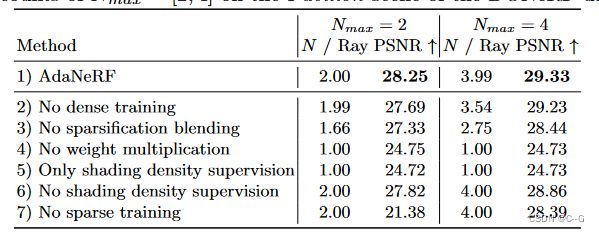
AdaNeRF 对 sample 网络和 shading 网络进行端到端的训练，并逐步减少每个视图射线所需的样本，通过累积RGB颜色的标准MSE损失来训练 shading 网络，sample 网络损耗由稀疏性损耗组成，稀疏性损耗包括与 shading 网络的输出密度匹配的 L1-loss，以及由 shading网络的MSE损耗派生的额外密度乘法项

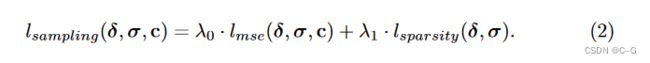
AdaNeRF采用 soft student-teacher 正则化训练方案，分为4个阶段

Dense Training

最初的密集训练阶段通过鼓励 sample 网络通过其所有输出趋向 $\delta =1$ 的 L1-loss 来输出密集预测，从而建立教师。这可以通过将网络权值直接初始化为输出1来替代，以提高训练速度，但可能会损失传播到采样网络的信息。如此，shading 网络都对整个输入空间进行采样，以提供对场景的初始估计，这防止了两个网络在后期阶段崩溃。

Sparsification

向 sample 网络引入了额外的 L1-loss，迫使大多数预测趋向于 0。在此阶段中，在强迫 sample 网络输出向 1 和 0 之间进行线性混合，并通过一个 L1-term 混合一个 soft student-teacher 正则化损失，以鼓励采样网络输出 $\delta$ 遵循与 $\sigma$ 类似的分布。从 $t_d$ 迭代持续时间的迭代 $t_0$ (以及给定的当前迭代 $t_c$ )，将稀疏化损失定义为

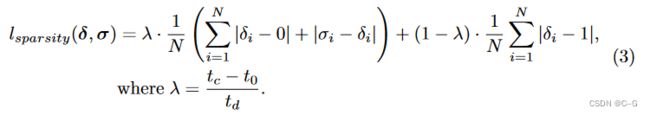
L1-term$|{\sigma }_i-{\delta }_i|$ 保证 sample 网络不会坍缩到单个常数0或1向量，强制 sample 网络遵循已建立的 shading 网络的场景表示，稀疏化阶段逐渐增加 sample 网络的稀疏性，导致更少的重要输出(随后在射线积累期间具有零贡献)

Sparse Training

为了让 shadomg 网络利用 sample 网络的稀疏性，在稀疏训练期间锁定 sample 网络的权重，尽管 shading 网络仍然沿着每条射线查询所有样本(如在密集训练阶段)，但现在可以自由更改已经被 sample 网络抑制的样本的输出(由于密度乘法)，这使得网络能够将其容量集中在那些实际上对输出有贡献的样本上

Fine-tuning

微调 shading 网络以获得所需的每条射线的最大样本数量，通常为2，4，8，16。这个阶段是快速的，因为每条射线的样本数量很少。微调可以提高质量，因为它完全删除了几乎对最终输出没有贡献的样本，并允许着色网络只关注有贡献的样本。此阶段为每个最大样本计数产生单独的 shading 网络，而所有都依赖于相同的 sample 网络

Real-time Rendering with Adaptive Sampling

通过启用每条射线的可变样本计数来进一步提高性能。这种自适应采样方案利用了AdaNeRF沿着射线最多只能包含一个样本的固定采样位置这一事实

首先，添加一个自适应采样阈值 $\tau$，它定义了采样网络预测的截止点 $\delta$。使能够在不需要多于几个样本的区域(如统一颜色的天空或简单的几何对象)保存 shading 网络评估，这反过来增加了管道的整体效率。

然后，将允许的最大样本数量限制为 $N_{max}$，并区分以下情况，这取决于 sample 网络预测的数量 $N_s$ 超过阈值 $\tau$

1. $N_s$ = 0:如果没有采样网络预测 ${\delta }_i$ 超过 $\tau$，将一个样本放置在与 sample 网络最大预测相对应的射线段的中心
2. $N_s$ ≤$N_{max}$:如果超过 $\tau$ 的 sample 网络预测 ${\delta }_i$ 的数量最多为$N_{max}$，将样本放置在它们所有段的中心。
3. $N_s$ > $N_{max}$:如果超过 $\tau$ 的 sample 网络预测的数量 ${\delta }_i$ 大于允许的最大样本数量 $N_{max}$，将每个样本放置在$N_{max}$ 最大预测的中心。

这种自适应采样方案可以使用 warp通信原语在gpu上有效实现，与首先需要从概率密度函数生成累积分布函数的典型重要性采样设置相比，能够进一步提高效率。请注意，所提出方法是第一个依赖于体集成的神经表示，并且(1)可以降至每条射线只有一个样本;(2)支持每条射线的可变样本计数，而不需要空间数据结构

实验

在Nvidia RTX 3090，shading 网络和 sample 网络都是 8 层 256 大小的mlp网络结构，使用Adam优化器，学习率为$5e^{-4}$，dense training 进行25k次迭代，sparsification 进行50k次迭代，sparse training 进行225k次迭代，fine-tuning 进行300k次迭代，损失函数各项权重为，${\lambda }_0=0.001，{\lambda }_1=1.0$，$\tau$在[0.05,0.40] 之间，采样点数量 N = [8,16]

消融实验

$\tau$大小的影响

实验数据结果

Limitations

尽管AdaNeRF已经在真实世界的数据上取得了很好的结果，但评估没有对相机参数进行优化，因此可能会受到输入数据不完全一致的影响。特别是对于非常低的样本计数，获得精确的表面信息对于实现良好的质量至关重要，并且为相机参数和/或照明的一致性添加额外的优化步骤可以进一步改善结果。其次，自适应采样的阈值，以及主优化函数的权重(最大化采样网络的稀疏性同时防止崩溃)影响AdaNeRF的稀疏性，影响整体质量和实时性。虽然这些参数可以相当稳健地应用于不同的数据集，但为了获得最佳性能，建议使用网格搜索。未来，可以从数据中学习这些参数，以节省超参数调优的时间。