PD我是你的真爱粉

从广义线性回归推导出逻辑回归

从广义线性回归推导出逻辑回归(LogisticRegression) – 潘登同学的Machine Learning笔记

文章目录

从广义线性回归推导出逻辑回归(LogisticRegression) -- 潘登同学的Machine Learning笔记
Logistic回归
广义线性回归
- 指数族分布（The exponential family distribution）
- - 推导说明伯努利分布是指数族分布
  - sigmoid函数
  - 回看多元线性回归
Loss函数的推导与求解
- 采用最大似然估计MLE来构造损失函数
- 求解Loss的最小值
- 直观感受Loss函数的形状
Logistic的实际应用
- 实战Logistic对鸯尾花的分类

Logistic回归

总目标：分类

逻辑回归就是在多元线性回归基础上把结果缩放到 0 到 1 之间。 $h_{\theta}(x)$ 越接近1 越是正例, $h_{\theta}(x)$ 越接近 0 越是负例,根据中间 0.5 分为二类;

模型：
$\hat{y} = h_{\theta}(x)= g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}}$

$\hat{y}$ 值：概率含义( $\hat{y}$ 越大说明分成正例的概率越大)

分类器的本质就是要找到分界,所以当我们把 0.5 作为分界时,我们要找的就是
$\hat{y} = h_{\theta}(x) = \frac{1}{1+e^{-\theta^Tx}} = 0.5$
的时候 $\theta$ 的解, 即 $\theta^Tx = 0$ 的解；

而这个函数也称为sigmoid函数;

优化目标：分类的越精确越好, 分对的越多越好

很自然而然的可以想到loss函数大概就是: 分对的概率取个负数(loss越小越好)
$L(\theta) = -\sum_{i=1}^{m}(y_{i}\log h_{\theta}(x_{i}) + (1-y_{i})\log (1-h_{\theta}(x_{i}))$
这个Loss函数也称为交叉熵;

注意： 这里的y是标签值(0代表负例, 1代表正例), 而 $h_{\theta}(x^{i})$ 才是预测值；

方便理解起见,考虑这样一种完美情况:

这个分类器把所有例子都分对了, 且分类器给出的指标特别完美, $\hat{y}$ 的值就是0或1, 没有不确定的因素存在;
那么当标签 $y^i$ 是1的时候, 我们的预测值 $\hat{y^i}=h_{\theta}(x^{i})$ 也是1, 两者相乘为1; 后一项 $(1-y^{i})\log (1-h_{\theta}(x^{i})$ 自然是0;
那么当标签 $y^i$ 是0的时候, 我们的预测值 $\hat{y^i}=h_{\theta}(x^{i})$ 也是0, 两者相乘为0; 后一项 $(1-y^{i})\log (1-h_{\theta}(x^{i})$ 自然是1;

所以无论标签值为多少, 求和的每一项都是1, 前面又有负号,那么Loss函数就是最小的,就是-m; (不可能存在 $(y^{i}\log h_{\theta}(x^{i}) + (1-y^{i})\log (1-h_{\theta}(x^{i}))$ 比1大的情形,因为标签是0和1, $y^{i}$ 是概率值, 这个式子其实就是0和1的加权平均, 最大值显然是1)

后面还会详细讲loss函数, 先有初步感知即可;

广义线性回归

考虑一个分类或回归问题，我们就是想预测某个随机变量 y，y 是某些特征(feature)x 的函数。为了推导广义线性模式，我们必须做出如下三个假设:

$p(y|x;\theta)$ 服从指数族分布
给定 $x$ ,我们的目的是为了预测 $T (y)$ 在条件 $x$ 下的期望, 一般情况下 $T (y) = y$ , 这就意味着我们希望预测
$h (x) = E [y ∣ x] (h 表示模型)$
参数 $\eta$ 和输入x是线性相关的: $\eta = \theta^Tx$
`

指数族分布（The exponential family distribution）

指数族分布有：高斯分布、二项分布、伯努利分布、多项分布、泊松分布、指数分布、 beta 分布、拉普拉斯分布、gamma 分布。对于回归来说,如果因变量 y 服从某个指数族分布,那么我们就可以用广义线性回归来建模。比如说如果 y 是服从伯努利分布,我们可以使用逻辑回归（也是一种广义线性模型）。

指数族分布的一般形式
$P(y;\eta) = b(y) e^{(\eta^TT(y)-a(\eta))}$
其中:

$\eta$ 是自然参数(natural parameter,also called theoretical parameter)
T(y) 是充分统计量(sufficient statistic),一般情况下就是 y
$a(\eta)$ 是对数部分函数（log partition function）,这部分确保 Y 的分布 $P(y;\eta)$ 计算的结果加起来（连续函数是积分）等于 1

推导说明伯努利分布是指数族分布

伯努利分布
$P(y;p) = p^y(1-p)^{1-y}$
将上式写成指数形式
$\begin{aligned} P(y;\eta) & = e^{y \log p+(1-y)\log(1-p)} \\ & = e^{(\log(\frac{p}{1-p})y+\log(1-p))} \\ \end{aligned}$
对应回指数族分布的一般形式:

$\eta = \theta^Tx = \log \frac{p}{1-p}$

则有:
$e^{\theta^Tx} = \frac{p}{1-p} \\ \begin{aligned} \Rightarrow p & = e^{\theta^Tx} - e^{\theta^Tx} \cdot p \\ & = \frac{e^{\theta^Tx}}{1+e^{\theta^Tx}} \\ & = \frac{1}{1+e^{-\theta^Tx}} \\ \end{aligned}$

诶！！这不就是sigmoid函数吗？

然后再回想这个二分类本质到低是啥？

二分类不就跟赌大小一样嘛？要么是大,要么是小;

那这个二分类任务不就可以看成伯努利分布吗？

如果p就是预测正确的概率, 那预测正确的数量y的概率密度函数不就是 $p^y(1-p)^{1-y}$ 嘛…

sigmoid函数

sigmoid函数的作用

逻辑回归就是在多元线性回归基础上把结果缩放到 0 到 1 之间。 $h_{\theta}(x)$ 越接近1 越是正例, $h_{\theta}(x)$ 越接近 0 越是负例,根据中间 0.5 分为二类; 所以sigmoid函数的作用就起到非线性变换的目的;

注意：这始终是广义线性回归模型, 线性回归就是 $y=\theta^Tx$ , 我们想求解的永远是 $\theta$ 而不是这个sigmoid;

回看多元线性回归

在多元线性回归中, 我们不是假设误差 $\varepsilon$ 服从正太分布嘛;

正态分布也是一种指数分布;
$\begin{aligned} f(\varepsilon_i|\mu,\sigma^2) &= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(\varepsilon_i-\mu)^2}{2\sigma^2}}\\ &= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{y^2}{2\sigma^2}}\cdot e^{\frac{2\mu y-\mu^2}{2\sigma^2}} \end{aligned}$
其中, 乘号前面视为 $b (y)$ , $\frac{2\mu}{2\sigma^2}$ 视为 $\eta$ , y视为 $T (y)$ , $\frac{\mu^2}{2\sigma^2}$ 视为 $a(\eta)$ ;

所以多元线性回归的形式就是
$\hat{y} = \eta = \theta^Tx$

Loss函数的推导与求解

我们的目标, 根据已知的 $x, y$ ,找到一组 $\theta$ 使得 $x$ 作为已知条件下y发生的概率最大;

$\begin{cases} g(\theta, x_i), 当y_i = 1时 \\ 1 - g(\theta, x_i), 当y_i = 0时 \\ \end{cases}$
( $g(\theta, x_i)$ 就是 $\hat{y}$ , 也就是 $h_{\theta}(x_i)$ )

也可以这样理解

$\hat{y}\Downarrow$ $y\Rightarrow$	0	1
0	$g(\theta, x_i)$
1		$g(\theta,x_i)$

将上式写在一条式子中
$P(预测正确)=g(\theta, x_i)^{y_i} \cdot (1 - g(\theta, x_i))^{1-y_i}$
改写成熟悉的形式
$P(y|x;\theta)=(h_{\theta}(x))^{y} \cdot (1 - h_{\theta}(x))^{1-y}$

采用最大似然估计MLE来构造损失函数

最大化正确分类的概率
$\begin{aligned} {\Bbb{L}(\theta)} &= \prod_{i=1}^{m} P(y_i|x_i;\theta)\\ &= \prod_{i=1}^{m}(h_{\theta}(x_i))^{y_i} \cdot (1 - h_{\theta}(x_i))^{1-y_i}\\ \end{aligned}$
取对数, 将连乘变为连加
$\begin{aligned} \log {\Bbb{L}(\theta)} = \sum_{i=1}^{m}[y_i \log h_{\theta}(x_i) + (1-y_i)\log(1 - h_{\theta}(x_i))] \end{aligned}$
上面求最大, 下面求最小(得出Loss function)
$\sum_{i=1}^{m}[y_i \log h_{\theta}(x_i) + (1-y_i)\log(1 - h_{\theta}(x_i))]$

求解Loss的最小值

先对sigmoid函数求导
$\frac{1}{1+e^{-z}} \\ \begin{aligned} g'(z) &= e^{-z}\frac{1}{(1+e^{-z})^2}\\ &= \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})\\ &= g(z)(1-g(z))\\ \end{aligned}$
回到对Loss的求导
$\begin{aligned} \frac{\partial}{\partial \theta_j}Loss &= -\sum_{i=1}^{m}[y_i \cdot \frac{1}{h_{\theta}(x_i)} \cdot \frac{\partial h_{\theta}(x_i)}{\partial \theta_j} - (1-y_i) \cdot \frac{1}{1 - h_{\theta}(x_i)} \cdot \frac{\partial h_{\theta}(x_i)}{\partial \theta_j}] \\ &= -\sum_{i=1}^{m}[y_i \cdot \frac{1}{h_{\theta}(x_i)} \cdot - (1-y_i) \cdot \frac{1}{1 - h_{\theta}(x_i)}]\frac{\partial h_{\theta}(x_i)}{\partial \theta_j} \\ &= -\sum_{i=1}^{m}[y_i \cdot \frac{1}{g(\theta^Tx_i)} \cdot - (1-y_i) \cdot \frac{1}{1 - g(\theta^Tx_i)}]g(\theta^Tx_i)(1-g(\theta^Tx_i)) \frac{\partial \theta^Tx_i}{\partial \theta_j}\\ &= -\sum_{i=1}^{m}[y_i(1-g(\theta^Tx_i))-(1-y_i)g(\theta^Tx_i)]x_i^j \\ &= -\sum_{i=1}^{m}[y_i-g(\theta^Tx_i)]x_i^j \\ &= \sum_{i=1}^{m}[h_{\theta}(x_i) - y_i]x_i^j \\ \end{aligned}$
注意：其中 $x_i^j$ 是因为对第i个样本的第j个参数求导, 所以 $x_i^j$ 其实就是数据矩阵中的 $x_{ij}$ ;
欸！！！这个Loss函数怎么跟多元线性回归那么相似呢？

因为都是广义线性回归, 所以长的都差不多;

直观感受Loss函数的形状

采用了一个breast_cancer的数据集, 然后里面的数据的含义就不解释了(~~过于敏感~~), 就只是画loss函数, 与真正的分类任务还差的比较多; (因为一旦维度高了之后,loss函数就画不在3维空间里了)

话不多说, 上代码!!!

#%%逻辑回归loss图像
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
data = load_breast_cancer()
x,y = scale(data['data'][:,:2]),data['target']   #这里为了方便画图，所以只取x的两列
#求出两个维度对应的数据在逻辑回归算法下的最优解
lr = LogisticRegression(fit_intercept=False)  #为了方便画图，不加截距项
lr.fit(x,y)
#把参数取出来
w = lr.coef_

#已知w的情况下，传进来数据x，返回数据的y_predict
def p_theta_function(feature,w):
    Z  = feature.dot(w.T)     #Z = xθ
    return 1/(1+np.exp(-1*Z))


def loss_fuction(samples_features,samples_labels,w):
    result = 0
    #遍历数据集中的每一条数据，并且计算每条样本的损失，加到result身上得到整体数据集损失
    for feature,label in zip(samples_features,samples_labels):
        #这是计算一条样本的y_predict
        p_result = p_theta_function(feature,w)
        loss_result = -1*label*np.log(p_result) - (1-label)*np.log(1-p_result)
        result += loss_result
    return result
   
w1_space = np.arange(w[:,0]-0.6,w[:,0]+0.6,1.2/49)
w2_space = np.arange(w[:,1]-0.6,w[:,1]+0.6,1.2/49)
w1,w2 = np.meshgrid(w1_space, w2_space)
w_list = []
for i in range(50):
    temp = []
    for j in range(50):
        temp.append(loss_fuction(x,y,np.array([w1[i][j],w2[i][j]])))
    w_list.append(temp)
    
result = np.array(w_list)

fig=plt.figure()
ax1 = plt.axes(projection='3d')
ax1.contour(w1,w2,result,30)
ax1.view_init(elev=90., azim=140)
plt.show()

fig=plt.figure()
ax2 = plt.axes(projection='3d')
ax2.plot_surface(w1,w2,result,rstride = 1, cstride = 1,cmap='rainbow')
ax2.view_init(elev=20., azim=140)
plt.show()

结果图像:

Logistic的实际应用

贯彻Machine Learning的一致思路, 当然少不了梯度下降和正则项;

Logistic的实际求解是通过梯度下降解决的, 这里不再细说;

含正则项的Logistic的Loss函数

$-\sum_{i=1}^{m}[(h_{\theta}(x_i))^{y_i} + (1 - h_{\theta}(x_i))^{1-y_i}] + \frac{\lambda}{2}\sum_{i=1}^{n} \theta_j^2$

其偏导为

$\frac{\partial}{\partial \theta_j}Loss = \sum_{i=1}^{m}[h_{\theta}(x_i) - y_i]x_i^j + \lambda \theta_j$

实战Logistic对鸯尾花的分类

目标:将数据分为属于setosa和不属于setosa

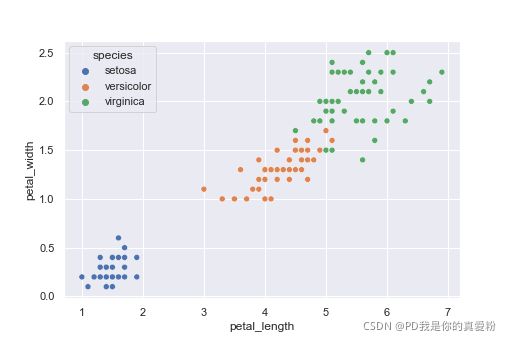
绘图查看 花瓣长度和花瓣宽度与鸯尾花种类的关系