「游戏」寻路算法之A Star算法原理及实现

前言

自动寻路是在一些如MMORPG等类型游戏中常见的一种功能，其给了玩家良好的游戏体验，使得玩家在游戏过程中省去了大量游戏坐标点的记录以及长时间的键盘操作，不必记忆坐标，不必担心迷路，用最快捷的方法移动到指定地点。

寻路算法（自动寻路算法，下同），其实可以看作是一种路径查找算法以及图搜索算法，图搜索（Graph Search）算法是用于在图上进行一般性发现或显式地搜索的算法。这些算法在图上找到出路径，但没有期望这些路径是在计算意义上是最优的。

路径查找算法（Pathfinding）是建立在图搜索算法的基础上，它探索节点之间的路径，从一个节点开始，遍历关系，直到到达目的节点。这些算法用于识别图中的最优路由，算法可以用于诸如物流规划、最低成本呼叫或IP路由以及游戏模拟等用途。

常见的路径搜索算法和图搜索算法有：A*（A Star）算法、Dijkstra算法、广（深）度优先搜索、最佳优先搜索、Jump Point Search算法等，今天本文主要讲解的是A*（A Star）算法的原理以及实现。

常见搜索算法

Dijkstra算法

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止¹。

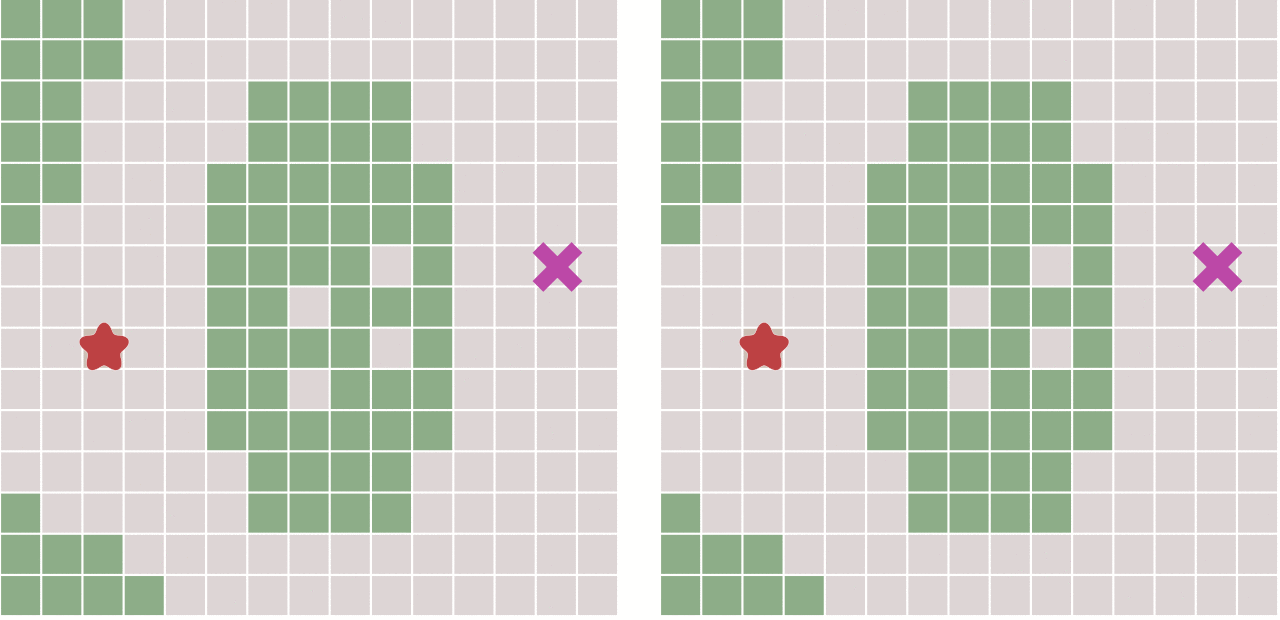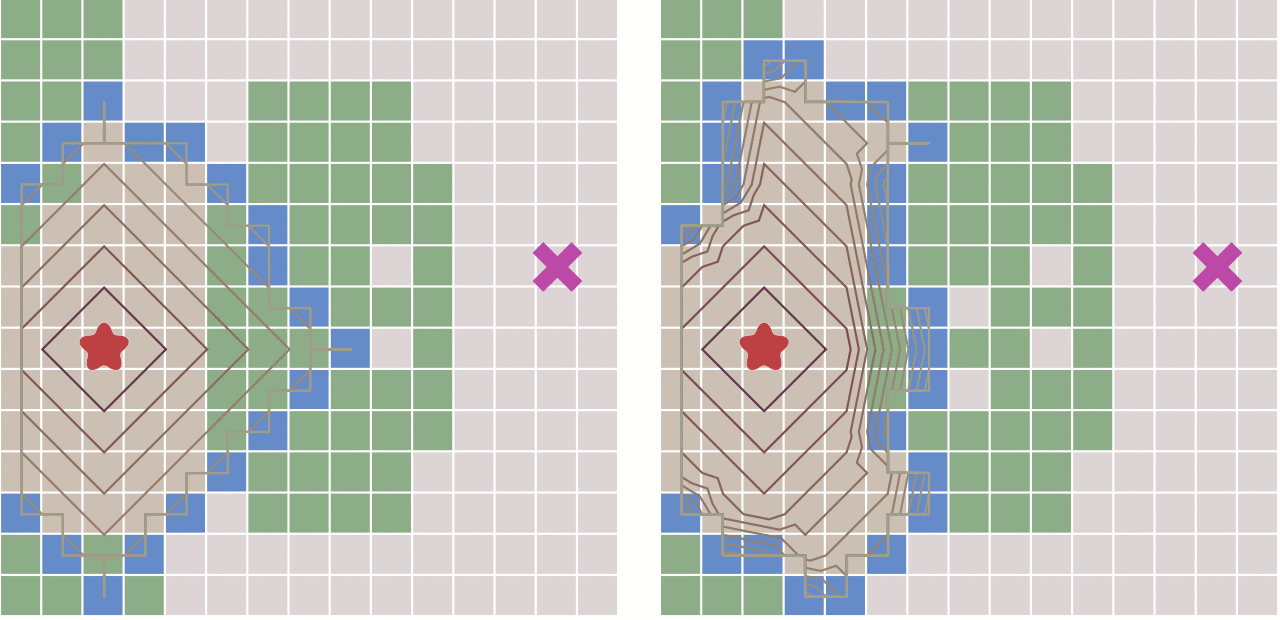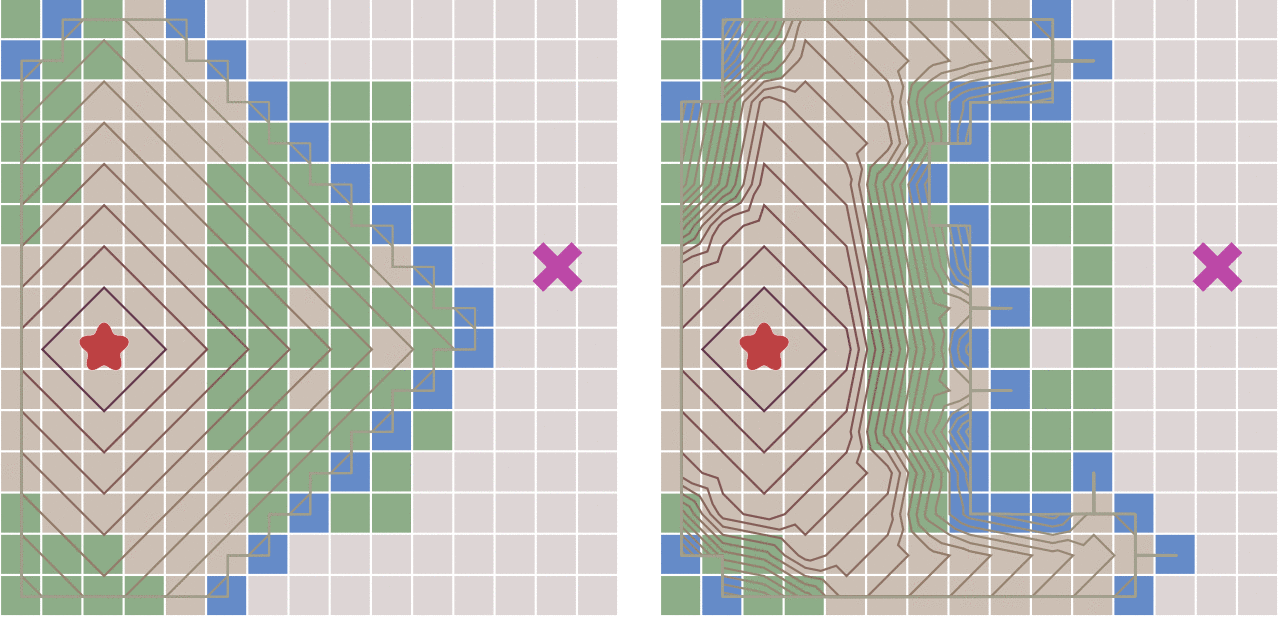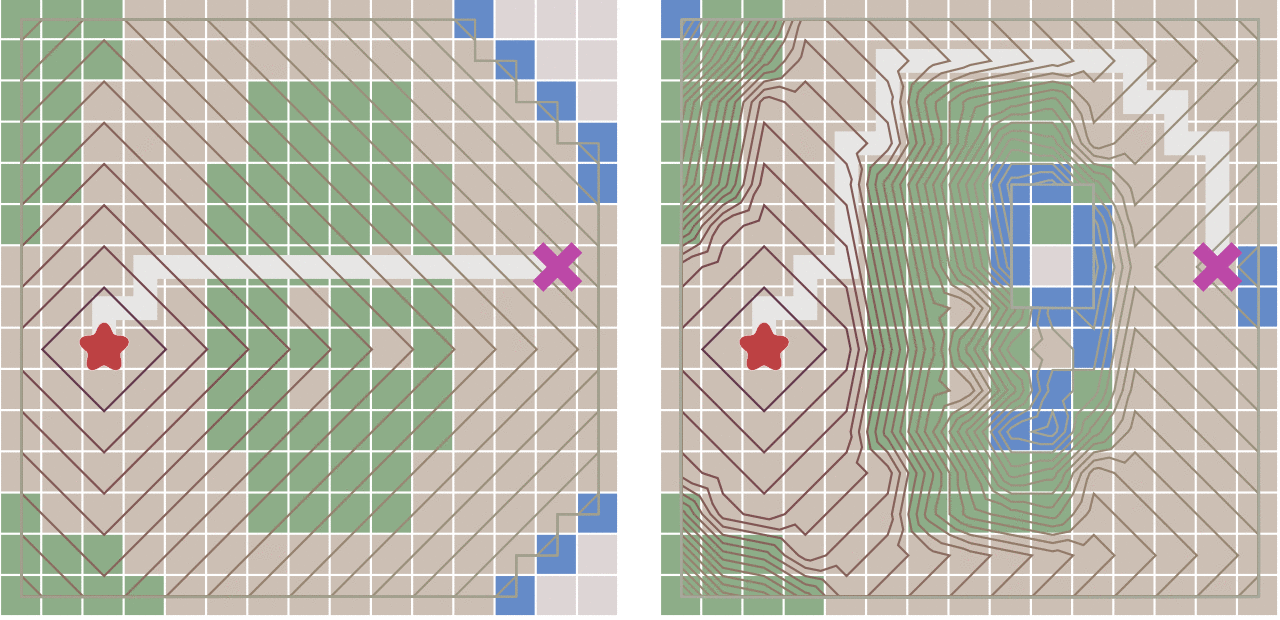
在游戏中（仅以2D为例），我们把某个场景的地图按照一定的规则划分成一个个的小格子，每个格子代表一个可用的坐标点，该坐标点有两种状态分别为：有效、无效。其中有效状态代表为该坐标点玩家可以正常通过，无效为该坐标点玩家无法到达，即当前坐标点可能存在阻挡物，如河流、山川、npc等，并且，以每个格子（以正方形为例）为中心可以分别向8个不同方向前进，在像每个方向前进时，所需的代价是不同的。

举个例子（后续的所有移动代价皆以此计算）

当玩家向自身8个方向中的横轴以及纵轴进行移动时（即向上、下、左、右），移动代价为10（别问为啥为10，拍脑门决定的）。

当玩家向自身八个方向中的对角方向进行移动时（即左上、左下、右上、右下），移动代价为横（纵）轴移动的1.4倍（因为正方形的对角线是边长约1.4倍）。

在使用该算法的时候需要选择一个周围8方向中，距离起点总移动代价最低的节点作为下一个要遍历的节点，一直到当前节点为终点或者无可用节点为止。那么此时就需要一个优先队列来保存当前节点的8方向中的可用节点、以方便的查找到移动代价最低的节点。

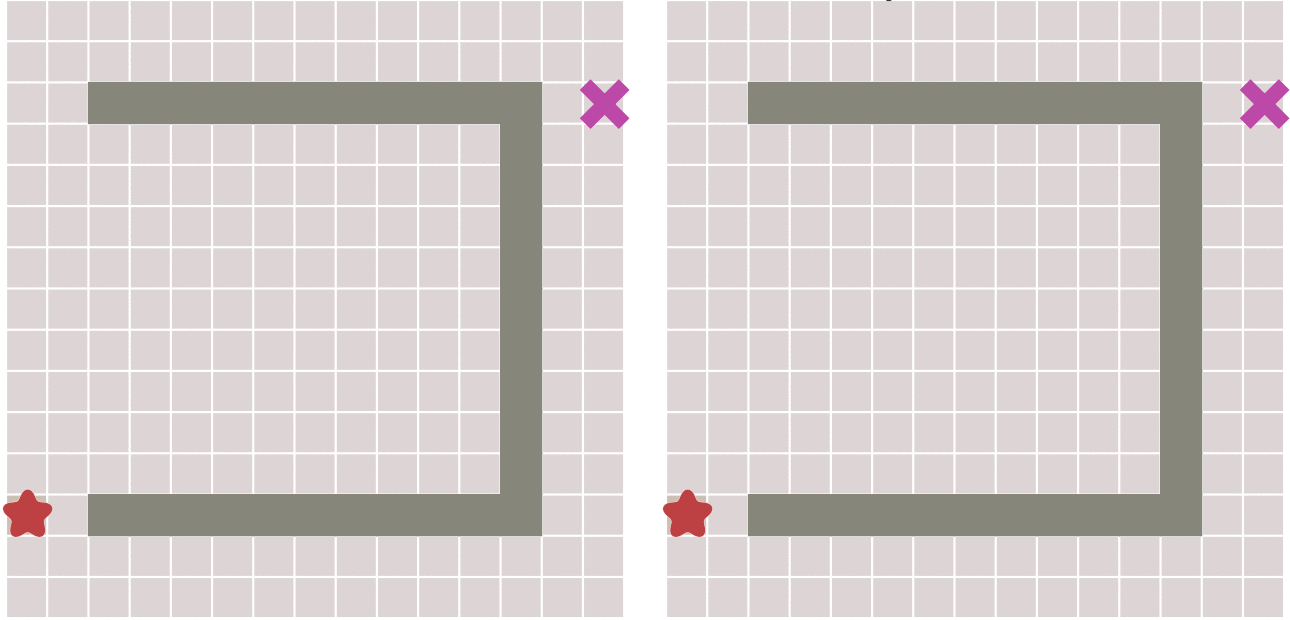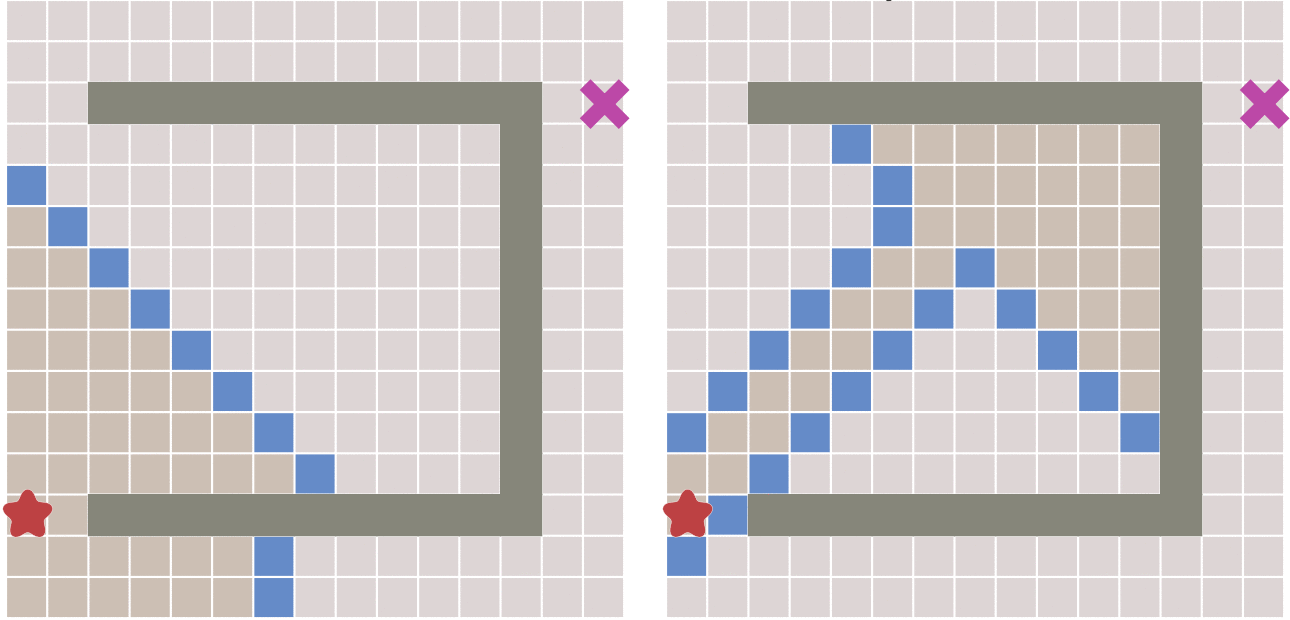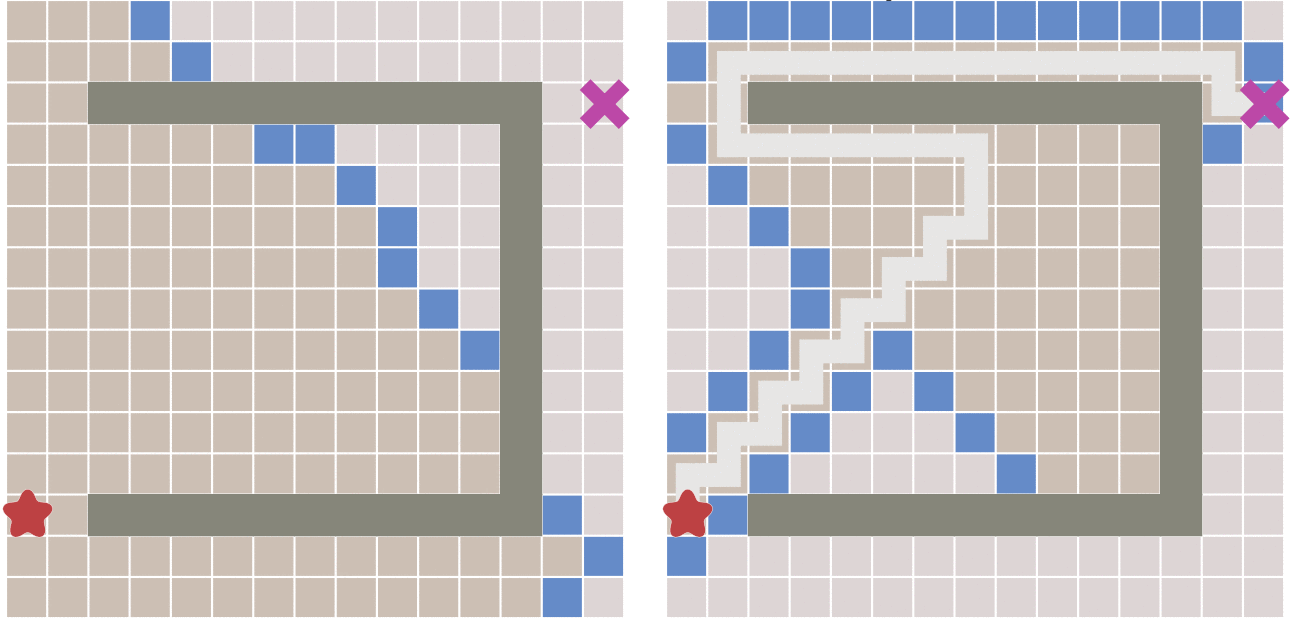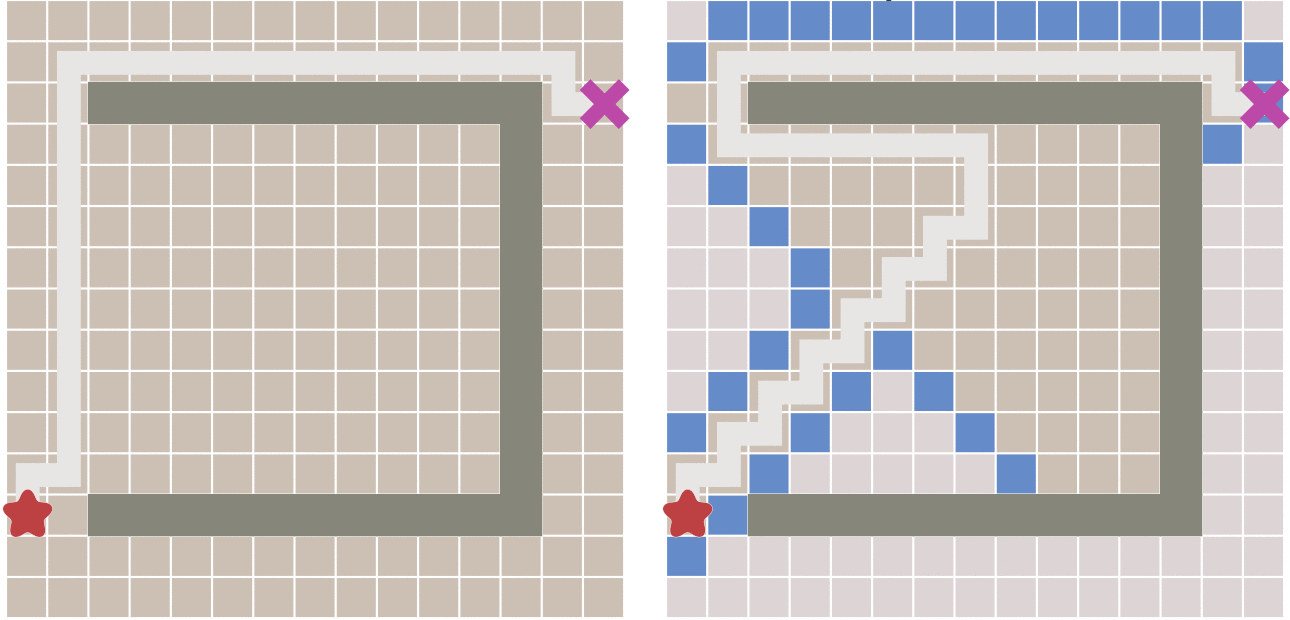
左图为BFS算法右图为Dijkstra算法（图侵删）

上图对比了不考虑节点移动代价差异的广度优先搜索与考虑移动代价的Dijkstra算法的运行图

应当注意，绝大多数的戴克斯特拉算法不能有效处理移动代价为负的图²。

最佳优先搜索算法（Best-First-Search）

最佳优先搜索算法是一种启发式搜索算法（Heuristic Algorithm），其基于广度优先搜索算法，不同点是其依赖于估价函数对将要遍历的节点进行估价，选择代价小的节点进行遍历，直到找到目标点为止。BFS算法不能保证找到的路径是一条最短路径，但是其计算过程相对于Dijkstra算法会快很多³。

所谓的启发式搜索算法，就是针对游戏地图中的每一个位置节点进行评估，从而得到相对来说最优的位置，而后再从这个最优为止再次进行搜索，直到符合终止条件或者超出地图范围为止，这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的预估是十分重要的。因此就需要使用启发函数来进行位置预估。

这个算法和Dijkstra算法差不多，同样也使用一个优先队列，但此时以每个节点的移动代价作为优先级去比较，每次都选去移动代价最小的，因为此时距离终点越来越近，所以说这种算法称之为最佳优先（Best First）算法。

接下来看一下运行事例：

图侵删

左侧为Dijkstra算法右侧为最佳优先搜索算法

最佳优先搜索算法相对于Dijkstra算法的问题在哪里呢？看一下中途有阻挡的时候的情况：

图侵删

左侧为Dijkstra算法右侧为最佳优先搜索算法

从上图中可以看出，当地图中存在障碍物的时候，最佳优先搜索算法并不能找到最短路径。

A Star 算法

A Star算法是一种在游戏开发过程中很常用的自动寻路算法。它有较好的性能和准确度。A*搜索算法（A* search algorithm）是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。常用于游戏中的NPC的移动计算，或网络游戏的BOT的移动计算上。该算法综合了最佳优先搜索和Dijkstra算法的优点：在进行启发式搜索提高算法效率的同时，可以保证找到一条基于启发函数的最优路径⁴。

启发公式

A Star算法也是一种启发式搜索算法那么其与最佳优先搜索算法一样需要一个启发函数左右计算移动代价的方法，那么A Star的启发函数公式为：
$$f(n)=g(n)+h(n)$$

解释下这个公式的各项的含义：

• h(n):从当前节点n到终点的预估的代价。
• g(n):从起始点到达当前节点n的代价。
• f(n):为当前节点n的综合的代价，在选择下一个节点的时候，其值越低，优先级就越高（因为代价小）。

关于启发函数中*h(n)公式的的选择，由于游戏地图中大部分都是被分为网格形式（即整个地图被拆分为多个正方形格子），那么此时就有3种可选的启发函数的h(n)*公式可用，分别为：

曼哈顿距离：出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

曼哈顿距离一般用在在移动时，只允许朝上下左右四个方向移动的情况下使用。

在平面中X1点到X2点的距离为其公式为：
$$d(i,j)=|X1-X2|+|Y1-Y2|$$
转换为程序语言如下，其中Cost为相邻两个节点移动所耗费的代价

func Manhattan(startX, startY, endX, endY float64) float64 {
	dx := math.Abs(startX - endX)
	dy := math.Abs(startY - endY)
	return Cost * (dx + dy)
}

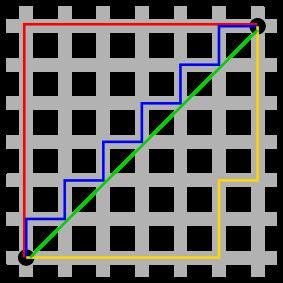
对角线距离： 如果你的地图允许对角线运动，则启发函数可以使用对角距离。它的计算方法如下：

其中HVCost是水平、垂直方向移动代价，SCost为倾斜方向移动代价

func  Diagonal(startX, startY, endX, endY float64) float64 {
	dx := math.Abs(startX - endX)
	dy := math.Abs(startY - endY)
	return HVCost*(dx+dy) + (SCost-2*HVCost)* math.Min(dx, dy)
}

欧几里得距离： 是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离），其公式为：
$$\sqrt[2]{(x2-x1{)}^2+(y2-y1{)}^2}$$

该公式为点(x1,y1)与点(x2,y2)之间的欧氏距离

func  Euclidean(startX, startY, endX, endY float64) float64 {
	dx := math.Abs(startX - endX)
	dy := math.Abs(startY - endY)
	return D * math.Sqrt(dx * dx + dy * dy)
}

在此文章中我们选择对角距离公式来作为启发函数求*h(n)*的公式。

启发函数可能对算法造成的影响⁵：

• 在极端情况下，当启发函数h(n) 始终为0，则将由g(n) 决定节点的优先级，此时算法就退化成了Dijkstra算法。
• 如果h(n) 始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n) 完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
• 在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

A Star算法执行过程

在搜索过程中，A Star算法需要遍历周围8方向的8个节点，并将之有效的节点（即可通过的节点）计算f(n)后放入一个优先级队列中，以便下次循环可以直接取出优先级最高的节点继续遍历，此时我们把这个优先级队列称呼为*OpenList***，另外A Star算法中也需要一个容器用来存储已经遍历过的节点、以防止重复的遍历，那么此时我们把这个容器称之为***CloseList***。

接下来本文讲按照步骤说明A Star算法每一步的执行过程：

1. 对***OpenList***和***CloseList***进行初始化，作者采用小根堆来作为***OpenList***的实现数据结构，采用HashMap作为***CloseList***的数据结构，其中Key为节点坐标值Value为空结构体。
2. 首先确定Start节点以及End节点，而后将Start节点放入***OpenList***中。
3. 从***OpenList***中取出一个节点Cur，如果Cur节点为End节点，则回溯当前节点结构中存储的父节点对象（像链表一样向前回溯）直到父节点对象为nil或者为Start节点，此时得到搜索到的路径，搜索结束返回。
4. 如果Cur节点非End节点则进行如下逻辑：
   1. 将当前X节点放入***CloseList***中，如果在取出Cur节点时未做删除操作的话那么则从***OpenList***中删除。
   2. 遍历Cur节点其周围8方向的所有额邻居可用节点、可用节点的条件为：
      1. 是可通过的节点。
      2. 未处于***CloseList***中。
   3. 计算当前的Cur节点的邻居可用节点，计算其f(n)值，设置其父节点为Cur节点，随后将其加入至*OpenList***中。
5. 循环执行3-4。直到找不到有效路径或找到End节点。

代码实现

本章代码采用Go1.16.2版本实现，主要展示的是搜索业务逻辑部分的代码。

// 优先队列
type PriorityQueue []*Node

func (receiver PriorityQueue) Len() int {
	return len(receiver)
}

func (receiver PriorityQueue) Less(i, j int) bool {
	return receiver[i].Fn() < receiver[j].Fn()
}

func (receiver PriorityQueue) Swap(i, j int) {
	receiver[i], receiver[j] = receiver[j], receiver[i]
}

func (receiver *PriorityQueue) Push(x interface{}) {
	*receiver = append(*receiver, x.(*Node))
}

func (receiver *PriorityQueue) Pop() interface{} {
	index := len(*receiver)
	v := (*receiver)[index-1]
	*receiver = (*receiver)[:index-1]
	return v
}

// 传入的是一个存放搜索路径的切片
// *tools.Node 是节点指针
func (receiver *FindAWay) doAStar(result *[]*tools.Node) {
   for receiver.OpenQueue.Len() > 0 {
     // 从 OpenList 里取出一个节点
      node := receiver.openGet()
     // 看看是不是终点
      if receiver.end.Equal(node.Position()) {
         receiver.statistics(node, result)
         return
      }
     // 节点放入CloseList
      receiver.closePut(node)
     // 进行具体处理
      receiver.azimuthProcessing(node)
   }
}

func (receiver *FindAWay) azimuthProcessing(node *tools.Node) {
  // 遍历当前节点的8个方向
  // tools.NodeFormula 是一个存有 计算8个方向坐标的函数数组
	for azimuth, f := range tools.NodeFormula {
    // Position 返回一个 存放了 XY字段的结构体代表节点坐标
		nearNode := tools.GlobalMap.GetNode(f(node.Position()))
    // 返回为nil代表节点超出边界
    // EffectiveCoordinate() 代表当前邻居节点是否可用，即是否可以通过
		if nearNode == nil || !nearNode.EffectiveCoordinate() {
			continue
		}
    // 查看当前邻居节点是否处于 CloseList里
		if _, ok := receiver.CloseMap[nearNode.Position()]; ok {
			continue
		}
    // 查看当前邻居节点是否处于 OpenList里
    // 这算是个优化，防止OpenList插入重复节点
		if _, ok := receiver.OpenMap[nearNode.Position()]; !ok {
      // 设置当前邻居节点的父节点为当前节点
			nearNode.SetParent(node)
      // 根据所处方位使用不同的移动代价计算Fn值
      
      // 此时 HVCost =10 
      // SCost = HVCost * 1.4
			switch tools.Azimuth(azimuth) {
        // 斜方计算
			case tools.LeftUp, tools.LeftDown, tools.RightUp, tools.RightDown:
				nearNode.CalcGn(tools.SCost).CalcHn(receiver.end.Position()).CalcFn()
        // 垂直、水平方向计算
			default:
				nearNode.CalcGn(tools.HVCost).CalcHn(receiver.end.Position()).CalcFn()
			}
      // 将当前邻居节点放入OpenList中
			receiver.openPut(nearNode)
		}
	}
}

结果测试

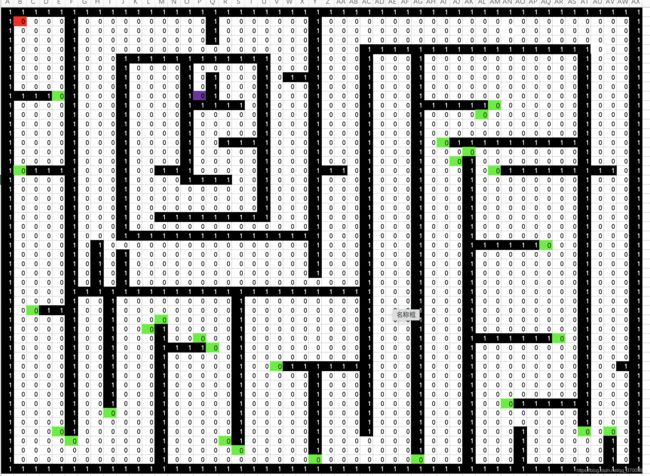
由于没有找到比较方便的实时现实库，所以就拿Excel做了一下，下面两个图为地图以及搜索后的结果图。

1为墙。

0为可通过的点。

5为得到的路径。

红色为起点

紫色为终点

绿色忘记删了，没有代表意义

下图为原地图：

下图为搜寻完毕的地图：

总结

A Star算法算是一个很简单的用于游戏中自动寻路的算法，但是其性能还有有些问题，主要问题在于其需要把每个节点的周围所有可用节点均插入至***OpenList***中，因此相对来说性能损耗几乎都在这个***OpenList***中，因此A Star算法有很多对其可以优化的算法。

日后作者将会写一篇关于针对A Star的优化算法即：JPS（jump point search）算法，该算法实际上是对A Star寻路算法的一个改进，A Star 算法在扩展节点时会把节点所有邻居都考虑进去，这样***OpenList***中点的数量会很多，搜索效率较慢。而JPS在A Star算法模型的基础之上，优化了搜索后继节点的操作。A Star的处理是把周边能搜索到的格子，加进OpenList，然后在OpenList中弹出最小值。JPS也是这样的操作，但相对于A Star来说，JPS操作***OpenList***的次数很少，它会先用一种更高效的方法来搜索需要加进***OpenList***的节点，从而减少***OpenList***中节点的数量。

我已开通自己的公众号【Echo的技术笔记】
日后的文章发布会主要在公众号上发布
希望各位关注一下
谢谢大家啦

---

1. Dijkstra算法 https://baike.baidu.com/item/%E8%BF%AA%E5%85%8B%E6%96%AF%E7%89%B9%E6%8B%89%E7%AE%97%E6%B3%95/23665989?fromtitle=Dijkstra%E7%AE%97%E6%B3%95&fromid=215612 ↩︎

2. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Section 24.3: Dijkstra’s algorithm. Introduction to Algorithms Second. MIT Press and McGraw–Hill. 2001: 595–601. ISBN 0-262-03293-7. ↩︎

3. 最佳优先搜索算法（Best-First-Search） https://www.jianshu.com/p/9873372fe4b4 ↩︎

4. A Star算法 https://zh.wikipedia.org/wiki/A*%E6%90%9C%E5%B0%8B%E6%BC%94%E7%AE%97%E6%B3%95 ↩︎

5. 路径规划之 A* 算法 https://paul.pub/a-star-algorithm/#id-dijkstra%E7%AE%97%E6%B3%95 ↩︎